4.3. Модель Бишопа-Хилла

С точки зрения физических гипотез модель Бишопа–Хилла практически не отличается от модели Тейлора, основное отличие состоит в ее математической строгости, наличии доказательств основных положений, принимаемых в модели Тейлора как постулаты. По существу, данная модель (равно как и модель Тейлора) является двухуровневой (мезо- и макроуровни). В модели макроуровня используется понятие поверхности текучести, f(S)=_s, при этом построение поверхности текучести осуществляется с применением модели мезоуровня; принимаются соотношения ассоциированного закона течения, . Полагается, что упругими деформациями можно пренебречь; пластическое деформирование осуществляется без изменения объема, D´^p = D^p. В теории используется также известный в теории пластичности принцип максимума работы: из всех возможных (т.е. не нарушающих условие текучести) напряжений действительное напряжение производит максимальную работу на приращении (пластических) деформаций.

В цитируемых работах Бишопа и Хилла доказывается также обратное (в определенном смысле) утверждение: если для заданного d напряжения Σ доставляют стационарное (или максимальное) значение работе по сравнению со всеми близкими напряжениями Σ^*, не выходящими за пределы поверхности текучести, то существует пластический потенциал, и он совпадает с поверхностью текучести; в случае максимальности работы соответствующая поверхность (изопотенциальная или поверхность текучести) является строго выпуклой.

На мезоуровне (уровне зерна) модель использует все основные предположения, принятые в модели Тейлора. Полагается, что упрочнение одинаково в активных и неактивных системах скольжения; однако при этом в активных системах возможно различие критических напряжений по противоположным направлениям скольжения, т.е. условие текучести имеет вид . В оригинальном варианте модели [73, 74] законы упрочнения практически не обсуждаются, поскольку не приводят к изменению структуры теории и ее основных соотношений.

Для монокристалла формулируется и доказывается принцип максимальности (максимума) работы. Пусть d – приращение деформации, реализующееся в монокристалле,  – тензор напряжений, вызывающий эту деформацию. Пусть имеется другой тензор напряжений ^*, не нарушающий условие текучести. Через d^(k) обозначим элементарные сдвиги по активным системам скольжения, так что , причем суммирование ведется только по номерам активных систем скольжения. На активных системах скольжения должно выполняться условие текучести, т.е. :  ^(k)= . Обозначим ^{* (k)} = :^* – сдвиговое напряжение в k-ой системе скольжения, соответствующее напряжению ^*. В силу предположения о допустимости ^* (т.е. ненарушении условия текучести) имеем:

.

Отметим также, что знаки d^(k) и ^(k) в данном случае всегда одинаковы и положительны (каждое из направлений в плоскости скольжения образует собственную систему скольжения). Тогда нетрудно установить следующее соотношение:

откуда

Соотношение представляет собой математическую запись принципа максимальной работы для монокристалла. Следует отметить, что здесь принцип доказывается, а не постулируется, как это принято в классической теории пластичности.

Отметим, что в физических теориях часто используются понятия геометрически и физически возможных систем сдвигов, или, при векторном представлении  в – соответствующих векторов сдвига. Вектор сдвига  называется геометрически возможным, если он реализует предписанную пластическую деформацию ε^p (аналогично – для приращений d и dε^p или скоростей ). Вектор d называется физически возможным, если он реализуем для данного напряженного состояния, т.е. в соответствующих системах скольжения выполняется условие текучести.

Для определения физически и геометрически возможных векторов (приращений) сдвига d в теории Бишопа–Хилла используется упомянутый выше принцип минимума сдвига. Пусть d – задаваемое приращение деформаций,  – тензор напряжений, инициирующий эту деформацию активизацией приращения сдвига d и удовлетворяющий условию текучести. Предположим, что d^* – вектор приращения сдвига, также эквивалентный d (т.е. геометрически возможный), однако не обязательно вызываемый некоторым напряжением, удовлетворяющим условию текучести (т.е. не являющийся физически возможным). Заметим, что в силу выполнения условия текучести для тензора  компоненты ^(k) вектора сдвиговых напряжений  в любой k-й системе скольжения не превосходят критического напряжения сдвига . Для геометрически и физически возможного вектора d в К активных системах скольжения ^(k) = , в остальных d^(l)=0. При этом в активных системах скольжения знаки d^(k) и ^(k) совпадают и положительны. Для геометрически (но не физически) возможного вектора d^* в каждой системе скольжения |^(k)|  , при этом знаки d*^(k) и ^(k) могут быть произвольными (т.е. и d*^(k), и ^(k) могут быть как положительными, так и отрицательными).

С учетом сказанного выше получаем:

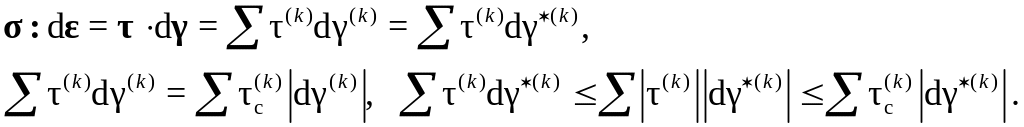
Следовательно,

Последнее соотношение представляет принцип минимума сдвига Тейлора, расширенный на случай неоднородного упрочнения ; иногда его называют принципом минимума работы. Полагая, что упрочнение одинаково во всех системах скольжения, из получаем:

,

представляющее собой математическую запись принципа минимума сдвига Тейлора: сумма абсолютных значений приращений физически и геометрически возможных сдвигов не превосходит суммы абсолютных значений приращений геометрически возможных сдвигов. Из доказательства следует также, что если существует более одной системы физически и геометрически возможных сдвигов, то сумма абсолютных значений приращений сдвигов во всех таких системах будет одинаковой.

Остановимся на соответствии двух сформулированных выше принципов, один из них – принцип максимума работы, второй – принцип минимума работы. При формулировке экстремальных принципов (более широко – вариационных принципов) важно различать параметры, которые можно изменять (перебирать, варьировать). В зависимости от этого величина, экстремальность которой устанавливается, может принимать максимальное или минимальное значение (а может не обладать экстремальными свойствами, в каждом конкретном случае последние надо устанавливать). Аналогичным образом дело обстоит и с рассматриваемыми принципами. В первом из них – принципе максимума работы, – варьируемой величиной является тензор напряжений, а бесконечно малое приращение деформаций является величиной заданной, неизменной в данный момент процесса. Во втором принципе ситуация «зеркально отражается»: тензор напряжений считается заданным, а варьируемыми параметрами являются бесконечно малые приращения сдвигов. Такие принципы в математической физике и вариационном исчислении называются двойственными (друг другу), из одного с помощью так называемого преобразования Лежандра следует другой, и наоборот (см., например, [20]).

Заметим, что в отличие от предположения Тейлора о том, что деформация реализуется сдвигом не более чем по пяти системам скольжения, здесь такого предположения не вводится, число активных систем скольжения ограничивается только числом возможных кристаллографических систем, что еще более усугубляет проблему неоднозначности определения сдвигов. Нетрудно видеть, что принцип минимума сдвига не позволяет определить единственный набор систем скольжения, он обеспечивает только «отбраковку» векторов сдвига, не являющихся физически возможными.

Хотя в физических теориях пластичности большое внимание уделяется построению моделей монокристаллов, главной задачей является формулировка конститутивной модели представительного объема макроуровня для поликристаллических материалов, без чего невозможна постановка и решение практически важных краевых задач МДТТ. В связи с этим неминуемо встают вопросы о переходе от переменных и соотношений мезоуровня к переменным и соотношениям макроуровня, о процедурах идентификации и верификации разрабатываемых моделей. При этом одним из важных компонентов модели становится принимаемая процедура осреднения.

Физические теории пластичности в их различных модификациях в значительной мере опираются на макроэксперименты. В частности, из макроэкспериментов определяются физические параметры (или часть из них), фигурирующие в описании микродеформирования; правильность основных положений ФТП проверяется, в конечном счете, также в опытах на макрообразцах. В связи с вышесказанным в замкнутой ФТП должны присутствовать подходы и соотношения, позволяющие связывать микро- и макропеременные.

При проведении экспериментов и интерпретации результатов в рассмотрение входят напряжения и деформации, осредненные по большому числу мезоэлементов (кристаллитов). Понятно, что интерпретация результатов макроэкспериментов с позиций ФТП существенным образом связана с принимаемой процедурой осреднения. Ниже рассматриваются некоторые аспекты принятого в теории Бишопа–Хилла подхода к осреднению, опирающегося на две основные гипотезы о связи микро- и макропараметров.

а). Измерения макропеременных осуществляются на таких объемах, что распределение ориентаций и упрочнения зерен в различных объемах отличаются несущественно. Иначе говоря, образец полагается однородным в макросмысле. Следует отметить, что это не исключает из рассмотрения анизотропные материалы, поскольку распределение ориентаций не обязательно равномерное, могут реализовываться случаи преимущественной ориентации в определенных направлениях.

В дальнейшем наименьший объем, обладающий подобными свойствами, будем называть «единичным» кубом (имеющим в действительности форму куба и единичные ребра).

б). Отсутствует корреляция между мезоскопическими напряжениями и положением на плоскости произвольного сечения единичной площади. Данное предположение позволяет представить результирующую мезонапряжений на такой единичной площадке как одиночную силу, приложенную в центре площадки. Выбирая далее декартову ортогональную систему координат, по компонентам определенной таким образом силы нетрудно получить компоненты тензора мезонапряжений, причем последний будет симметричным.

В случае если корреляция между мезонапряжениями и положением в единичном сечении существует, тензор мезонапряжений не обязательно симметричный. В этом случае уравнение баланса момента количества движения отличается от классического, в рассмотрение необходимо вводить тензор моментных напряжений; иначе говоря, от классического континуума следует переходить к обобщенному (например, континууму Коссера). Заметим, что подобное определение напряжений возможно на различных масштабных уровнях, включая используемый в некоторых вариантах ФТП так называемый «атомный» (представительный объем атомного уровня можно определить как объем совершенной кристаллической решетки, содержащей 10³–10⁶ атомов).

Рассмотрим связь кинематических характеристик мезо- и макроуровней, опираясь на геометрический смысл компонент тензора малых деформаций (в случае рассмотрения геометрически нелинейных проблем следует использовать аналогичные соотношения для тензора деформации скорости). Будем обозначать через (U, ε, Σ) мезоскопические (макроскопические) перемещения, деформации и напряжения. Тогда приращение тензора малых деформаций для «единичного» куба можно определить следующим образом:

,

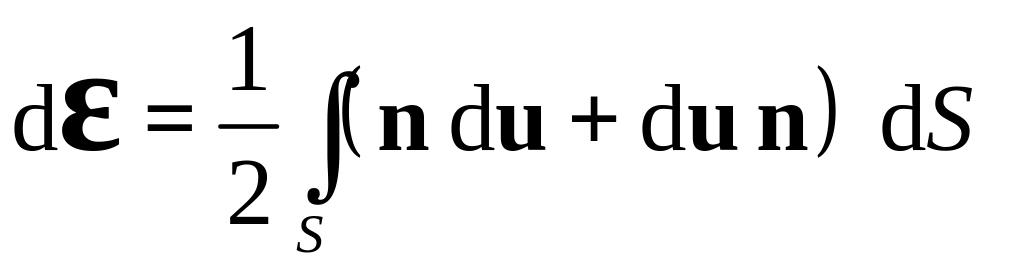где n – единичная внешняя нормаль к поверхности «единичного куба», S – его поверхность. В случае, если мезоскопические перемещения принимаются непрерывными дифференцируемыми функциями пространственных координат, из следует:

,

где интегрирование ведется по объему единичного куба. Отметим, что в случае произвольных («не нормализованных») размеров представительного объема правые части и следует делить соответственно на S и V.

Следует подчеркнуть, что мезопараметры представляют собой некоторые осредненные величины по подобъемам представительных мезообъемов. Иначе говоря, и на мезоуровне осуществлен переход к континуальному описанию.

Элементарная работа, совершаемая мезонапряжениями в представительном объеме, определяется соотношением:

,

вторая часть соотношения справедлива в случае непрерывности и дифференцируемости полей мезоперемещений и выполнении на мезоуровне однородного условия равновесия. Заметим, что компоненты мезонапряжений не обязательно должны быть непрерывными на произвольных поверхностях (например, границах зерен), для выполнения условий равновесия должны быть непрерывны только результирующие распределенные нагрузки на таких поверхностях.

В дополнение к двум предыдущим принимается гипотеза об отсутствии корреляции между распределением любых компонент тензора мезонапряжений и любыми компонентами вектора мезоперемещений в любом сечении (для простоты сечения берутся единичной площади).

В модели Бишопа – Хилла осреднение производится по единичной площади произвольного сечения:

.

Из последнего определения с учетом сформулированной выше гипотезы Бишопом и Хиллом доказано следующее соотношение:

.

Следует отметить, что доказательство этого соотношения не вызывает затруднений с учетом того, что в модели Бишопа–Хилла принята гипотеза Фойгта; по существу, в этом случае сводится к утверждению об идентичности осреднения тензора напряжений по объему и ₁.

С использованием последнего соотношения может быть доказан принцип максимума работы для поликристалла на основе принципа максимума для монокристалла, не прибегая при этом к понятию поверхности текучести поликристалла. Действительно, пусть ^* – мезонапряжения, не нарушающие условия текучести и удовлетворяющие однородному условию равновесия, Σ^* – осредненные напряжения. Тогда в соответствии с и имеем:

что и требовалось показать.

Аналогично доказывается принцип минимума сдвига для поликристалла. Пусть du и du^* – непрерывные с непрерывными первыми производными поля перемещений, удовлетворяющие условию сохранения объема ( ), имеющие одинаковые значения на поверхности единичного куба. Полагаем, что du ассоциировано с равномерным распределением мезонапряжений , удовлетворяющих условию текучести. Тогда:

,

или

При этом справедливы следующие равенства:

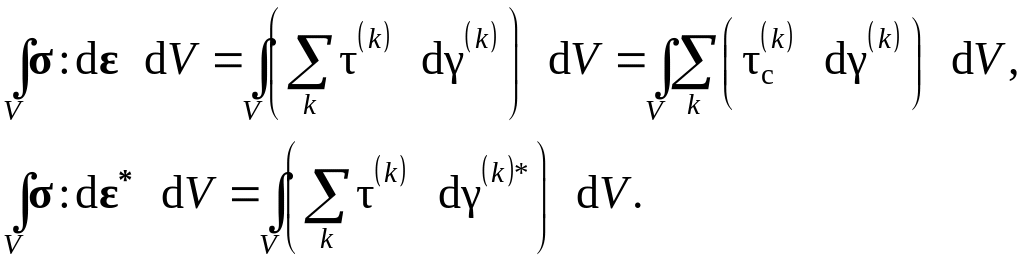
В силу того, что d^(k)* – геометрически возможны, но не обязательно физически возможны, в ₂ знаки ^(k) и d^(k)* могут быть различны, при этом , откуда получаем:

. (*)

В ₁ знаки ^(k) и d^(k) совпадают и положительны, на активных площадках , откуда следует:

.

Тогда получаем окончательно:

.

Полагая критические напряжения сдвига одинаковыми по агрегату, получаем принцип минимума сдвига для поликристалла:

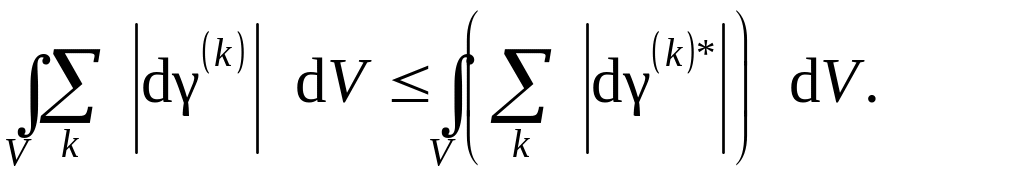
Комбинируя и , приходим к следующему соотношению:

.

Кроме того, справедливо неравенство:

,

где d^* соответствует некоторому перемещению dU^*. Напомним, что принципы максимума работы и минимума сдвига являются двойственными [20], и в этом смысле эквивалентны друг другу, один следует из другого.

Как следует из последних результатов, принцип максимума работы справедлив для агрегата из монокристаллических зерен в предположении, что деформирование в каждом из них осуществляется сдвигом по определенным системам скольжения. Тогда из ранее сформулированного (без доказательства) утверждения следует, что может быть построен пластический потенциал, совпадающий с функцией текучести. Но тем самым решается в принципе вопрос об установлении определяющих соотношений (с помощью принципа градиентальности).

Сопоставляя модель Бишопа–Хилла с ранее изложенной моделью Тейлора, нетрудно убедиться, что концептуальные положения обеих моделей практически совпадают (а следовательно – модели Бишопа–Хилла присущи те же недостатки, что и модели Тейлора); модель Бишопа–Хилла отличается более глубокой «математической оснащенностью». Вероятно, это является причиной того, что в последнее десятилетие модели, имеющие в основе те же гипотезы и положения, что и модель Тейлора, стали называть моделями «типа Тейлора–Бишопа–Хилла».

Несмотря на отмеченные выше недостатки моделей Тейлора–Бишопа–Хилла, они являются одними из наиболее широко используемых. В последние 10-15 лет модели этого класса часто применяются для анализа различных технологических процессов обработки металлов давлением и других распространенных технологических процессов. Пример применения модели для исследования процесса механической обработки (ортогонального резания) монокристаллической заготовки содержится в работе [85].

Дальнейшее развитие моделей этого класса связано, в частности, с совершенствованием математической основы моделей, модификацией соотношений теории для учета поворотов кристаллической решетки. Например, в работе [98] наряду с трансляционной (сдвиговой) модой деформирования идеально–пластического монокристалла предлагается ввести дополнительные параметры, характеризующие ориентацию кристаллической решетки (три угла Эйлера). В качестве ключевой гипотезы вводится предположение об аддитивном разложении градиента скорости перемещений на пластическую составляющую, определяемую скоростями сдвигов по активным СС, и спин решетки. Одну из известных трудностей – задания граничных условий для скорости поворота решетки, – автор предлагает избежать за счет задания так называемых «глобальных кинематических условий», согласно которым в исследуемом теле вводятся материальные направления с запрещенными поворотами (например, вдоль оси растягиваемого образца). Как представляется, указанные гипотезы не имеют достаточного физического обоснования даже для монокристаллов. Детальное изложение моделей Тейлора, Бишопа – Хилла и обзор работа по их применению содержится в статье [101].