4.2. Модель Тейлора

Вероятно, первой достаточно реалистичной попыткой установления связи - при одноосном нагружении поликристалла на основе соотношений для монокристалла можно признать модель Тейлора [164]. При её построении Тейлором использованы следующие гипотезы:

1. Поликристалл представляет собой агрегат из большого числа хаотично ориентированных (по равномерному закону) зерен.

2. Поведение каждого из зерен описывается жесткопластической моделью; деформации зерен осуществляются только кристаллографическим сдвигом по известным для данного материала кристаллографическим системам скольжения (СС).

3. Упрочнение одинаково во всех системах скольжения и определяются свойствами монокристалла.

4. Границы зерен имеют нулевую толщину, не осуществляют вклада в механизмы неупругого деформирования.

5. Деформации (или деформации скорости) полагаются однородными в пределах макроскопического представительного объема (гипотеза Фойгта), т.е. ^p(n) = <^p> =  (или dd^p(n)=<d^p>=D^p= D), n – номер кристаллита (зерна). Кроме того, поскольку деформации осуществляются сдвигом, в этом случае отсутствует изменение объема, т.е. ^p(n) = e^p(n) = <e^p> (или d´^p(n)= d^p(n), d´– девиатор тензора d).

В кристаллах с ГЦК и ОЦК решеткой число СС существенно превышает число независимых компонент девиатора деформаций (см. п. 3.1), что обусловливает неоднозначность определения сдвигов по СС по заданному девиатору деформаций. Указанное обстоятельство является одной из существенных трудностей построения физических теорий пластичности.

Для ее преодоления Тейлором был предложен эвристический принцип, суть которого состоит в следующем. Полагается, что любая деформация (или приращение деформации) осуществляется сдвигом по не более чем пяти независимым CC, определенным из условия минимальности суммарного сдвига . Представляющий по существу гипотезу, данный принцип минимума сдвига основывался на наблюдениях за поведением одиночных кристаллов.

Обозначим через приращение сдвига в n -ом зерне по k -ой CC (соответствующая скорость сдвига обозначается как ). Тогда принцип минимума сдвига математически записывается в виде

,

при этом в силу принятой гипотезы Фойгта должно выполняться ограничение

,

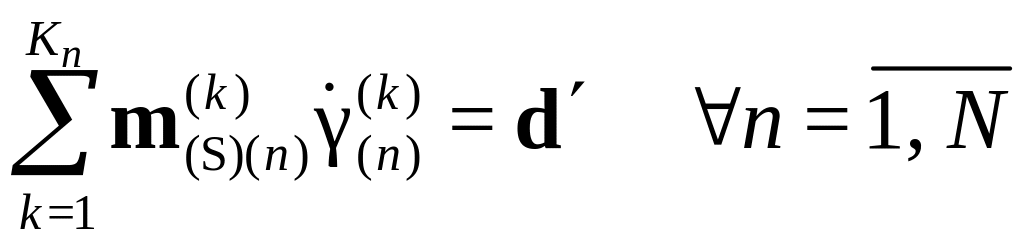где d´=D´ – предписанный (заданный в каждый момент деформирования) девиатор деформации скорости; здесь в обозначении ориентационного тензора появился индекс п, относящийся к номеру зерна; в дальнейшем он будет сохраняться только в случае, если из контекста не ясно, что ориентационный тензор относится к системам скольжения определенного зерна. Заметим, что в случае отказа от предположения об изотропном упрочнении в каждом из зерен принцип минимума сдвига трансформируется в принцип минимума мощности, согласно которому действительные скорости сдвига доставляют минимум мощности (по сравнению с кинематически возможными скоростями сдвигов):

.

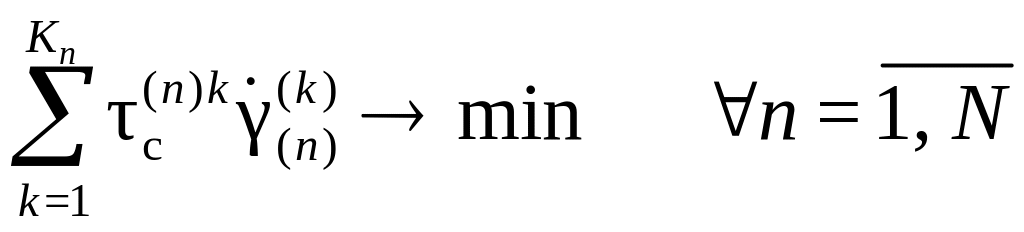Более подробно принцип минимума мощности рассмотрен ниже.

Как отмечено выше, критические напряжения сдвига в исходной модели Тейлора приняты одинаковыми во всех системах данного зерна и обозначаются как . Тогда элементарная работа dA^(п), произведенная в п-м зерне объемом V^(п), определяется соотношением:

,

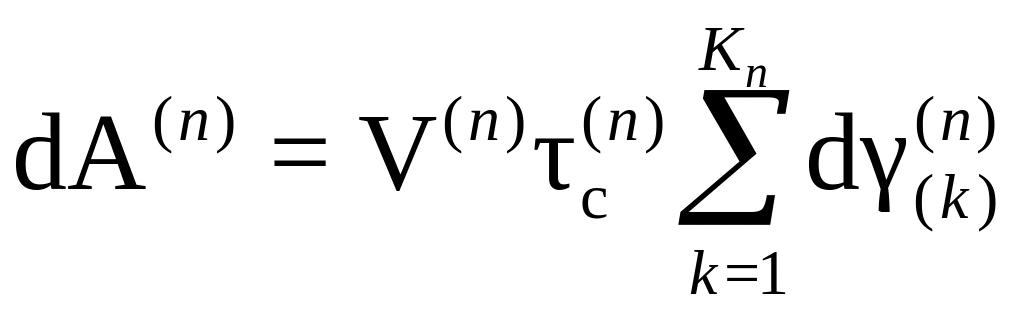где К_n – число активных систем скольжения в данном п-м зерне в рассматриваемый момент нагружения.

Элементарная работа dA, производимая на сдвигах по активным CC в агрегате из N монокристаллов, определяется следующим соотношением:

.

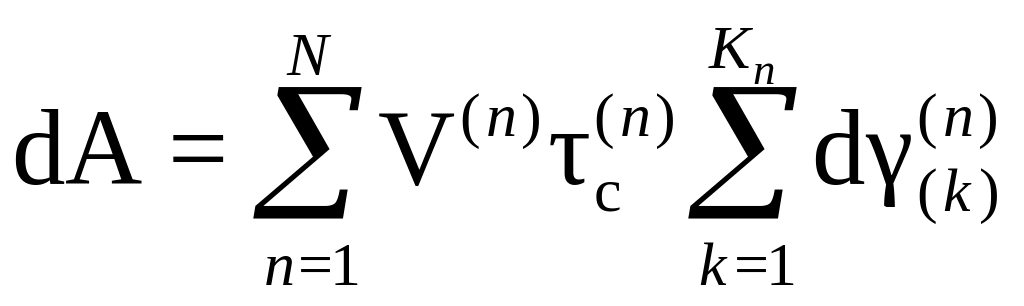Заметим, что в правой части суммирование по числу активных CC осуществляется от 1 до К_n, т.е. в различных зернах это число может быть различным (1 К_n 5).

В модели Тейлора полагается, что вся подводимая к образцу механическая энергия расходуется на совершение пластической деформации. В случае одноосного нагружения (при действии напряжения ₁₁) элементарная работа внешних сил в предположении одноосного макроскопического напряженно-деформированного состояния равна

. Тогда, приравнивая работу внешних напряжений и работу внутренних сдвиговых напряжений, получаем:

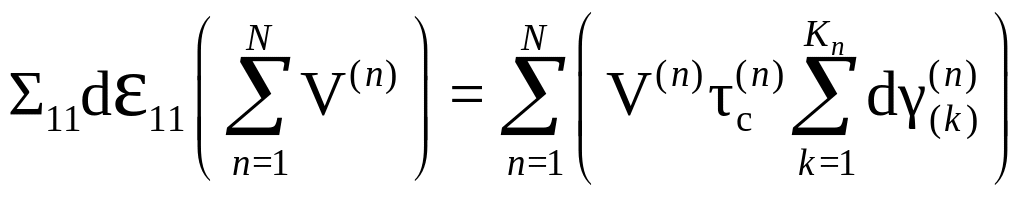
Предполагая, что все зерна имеют одинаковый объем, окончательно получаем:

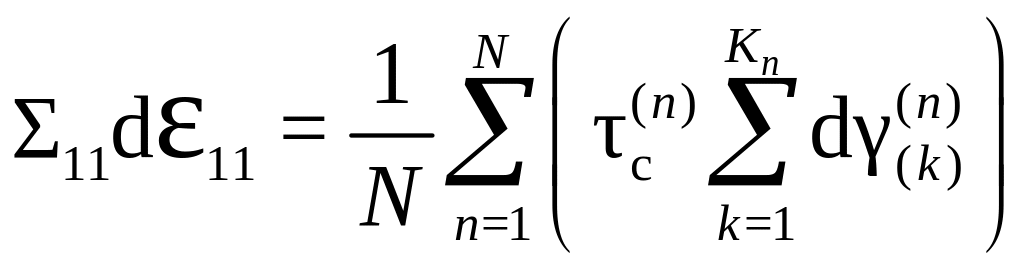
Последнее соотношение позволяет построить кривую одноосного нагружения поликристалла с использованием модели монокристалла. Процедура пошагового построения кривой состоит в следующем:

• Пусть кривая построена для определенной предшествующей (макро)деформации ₁₁, т.е. известны напряжения Σ₁₁ во все предшествующие моменты нагружения, накопленные сдвиги, критические напряжения сдвига во всех зернах; ориентация зерен полагается неизменной и известной.

• Задается достаточно малое приращение деформации Δ₁₁, являющееся одновременно приращением главной деформации Δ₁=Δ₁₁; из условия несжимаемости определяются два других главных значения приращений деформаций Δ₂=Δ₃= –1/2Δ₁ (при этом Δ₂=Δ₂₂, Δ₃=Δ₃₃, все остальные компоненты тензора Δ равны нулю). Следует подчеркнуть, что в данном случае главные оси тензоров  и Δ совпадают и неизменны. По заданному тензору Δ данного шага нагружения в каждом зерне определяются приращения сдвигов по активным СС, обеспечивающие минимальность приращения суммарного сдвига.

• По накопленным сдвигам (с учетом приращений на рассматриваемом шаге) определяются критические напряжения сдвига в каждом зерне 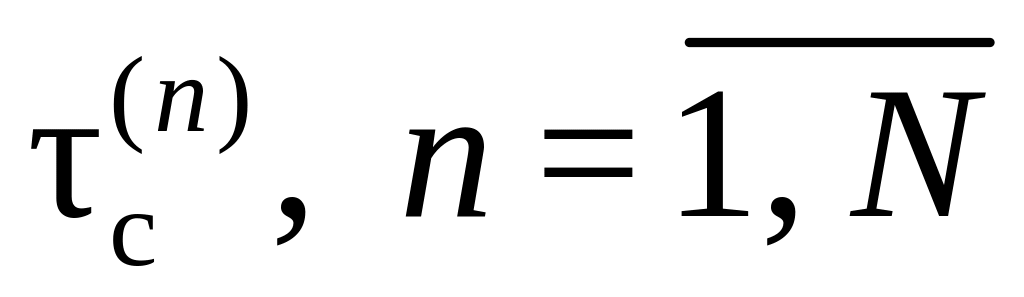, после чего легко определяется значение правой части и величина Σ₁₁.

Тейлор применил описанную процедуру для построения кривой одноосного деформирования алюминия (ГЦК–решетка). Результаты расчета хорошо согласуются с экспериментальными данными, что подтверждает приемлемость модели для рассмотрения, по крайней мере, одноосного нагружения.

Таким образом, модель Тейлора [164] сводится к минимизации мощности работы на сдвигах (в пространстве скоростей сдвигов) при ограничении , после чего для определения девиатора напряжений используется закон Шмида с ориентационными тензорами, соответствующими активным системам скольжения.

Постановку задачи минимизации мощности для каждого зерна можно переформулировать следующим образом. Введем обозначения (определив компоненты тензоров в базисе ЛСК и опуская знак симметризации (S)):

,

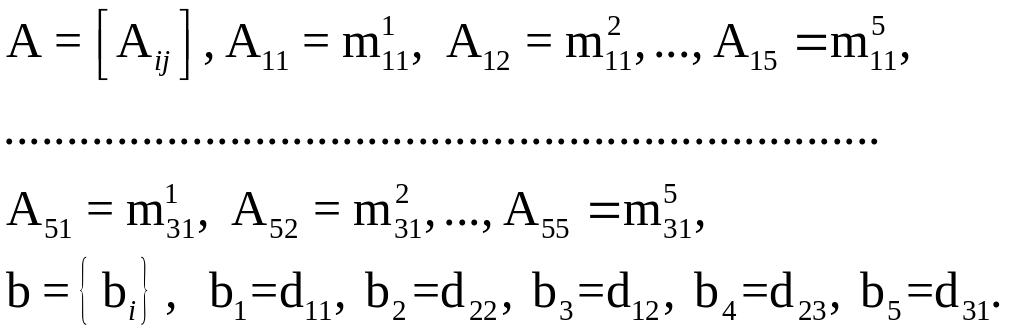
Тогда задачу – можно записать в канонической форме задачи линейного программирования [29]:

min c^Tx,

Ax=b, (А)

x 0.

Процедура решения следующая: из решения возможных для данного типа кристаллов систем линейных алгебраических уравнений (А₂) (каждая из систем содержит в общем случае 5 уравнений) определяются соответствующие наборы скоростей сдвигов; из них сразу «отбраковываются» решения, содержащие отрицательные компоненты вектора х. Из оставшихся «наборов» определяется удовлетворяющий (А₁). Достаточно подробно процедура решения, основанная на технике линейного программирования, рассмотрена в [176].

Отметим, что сформулированной выше классической задаче линейного программирования (А) можно, используя формализм линейного программирования [29], поставить в соответствие эквивалентную ей двойственную задачу:

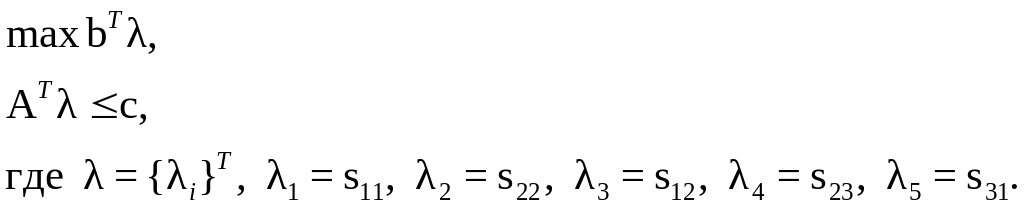(А_д)

Этот двойственный принцип максимума работы, в котором варьируемыми параметрами являются напряжения, был доказан в работах Бишопа–Хилла [73? 74] исходя из физики пластичности монокристалла. Задача максимизации мощности (А_д) также представляет собой задачу линейного программирования, решение которой соответствует одной их вершин многогранника текучести; из теории линейного программирования известна эквивалентность этих формулировок.

Заметим, что в собственно модели Тейлора девиатор напряжений вообще отсутствует, напряжения априори полагаются такими, что активизируют все необходимые для реализации предписанной скорости деформации системы скольжения, причем число СС равно числу независимых компонент девиатора напряжений. Компоненты девиатора напряжений определяются на втором этапе, после определения активных СС и скоростей сдвига по ним. Для этого используется закон Шмида, представляющий в этом случае систему линейных алгебраических уравнений относительно компонент девиатора напряжений (число уравнений равно числу активных систем скольжения).

Резюмируя, можно отметить следующие проблемы, возникающие при применении модели Тейлора:

• Неединственность определения совокупности 5 скоростей сдвига, реализующих предписанный девиатор скоростей деформаций.

• Возможное несоответствие напряженного состояния виду нагружения (например, при одноосном нагружении напряженное состояние может отличаться от одноосного).

• Невозможность определения тензора напряжений по скоростям девиатора деформаций, поскольку имеем материал со связью (несжимаемость).

• Не исключена ситуация, когда минимум мощности достигается на совокупности систем скольжения с числом нетривиальных скоростей сдвига, меньшем 5 (например, при совпадении систем скольжения с плоскостями и направлениями главных скоростей сдвига). Эта ситуация соответствует нахождению изображающей точки в пространстве напряжений (ИТН) на грани или ребре многогранника текучести. Ряд авторов трактует данную ситуацию как так называемое вырождение системы уравнений. Это представляется не совсем верным. Действительно, в модели Тейлора поиск осуществляется именно в вершинах многогранника и число уравнений должно соответствовать числу неизвестных компонент девиатора напряжений (случай большего числа упомянут выше). Однако в данном случае не дает критерия отбора единственного набора активных систем скольжения и решению с точки зрения минимума мощности сдвига удовлетворяют все ИТН в вершинах многогранника текучести, примыкающие к данной грани или ребру, хотя напряжения при этом существенно отличаются. Последнее возможно, например, в случае чистого сдвига при ориентации одной из систем скольжения в точности соответствующей сдвигу по данной системе.

• Невыполнение условий равновесия на границах зерен.

• Сложность реализации модели, связанная с необходимостью определения активных систем скольжения и сдвигов в них, доставляющих минимум суммарному сдвигу. Процедура решения данной задачи минимизации оказывается весьма трудоемкой.

• Неучет в модели Тейлора упругих деформаций.

Достаточно грубым является также предположение об однородности деформаций и напряжений в поликристаллическом агрегате, что не соответствует теоретическим (см., например, [156]) и экспериментальным результатам, особенно в случае сложного нагружения. В реальных процессах деформирования микродеформации и микронапряжения неоднородны даже в пределах каждого зерна и субзерна.

Заметим, что часть (п. 2, 3, 4) из указанных выше недостатков в известных авторам работах не отмечалась. Однако и отмеченных ранее оказалось вполне достаточно, чтобы стимулировать исследователей к совершенствованию модели Тейлора. В первую очередь появились работы, направленные на «подведение» под модель Тейлора более глубокой математической «базы», замена интуитивно высказанных положений математически строго доказанными. Значительное внимание в работах последнего десятилетия уделяется законам упрочнения по системам скольжения. Например, в работе [174] за основу принимается закон упрочнения типа Воуса, который модифицируется для учета взаимодействия дислокаций разных систем скольжения, в том числе – аннигиляции дислокаций при изменении направления нагружения. При этом основные положения и гипотезы модели Тейлора остались неизменными. К числу наиболее ярких работ этого направления относятся статьи Бишопа и Хилла [73, 74], подробно анализируемые ниже.