Основные обозначения

Е – модуль упругости

G – модуль Юнга

d_и – интенсивность скоростей деформаций

– главные инварианты тензора малых деформаций и его девиатора

– главные инварианты тензора напряжений Коши Σ и его девиатора S

К – модуль объемного сжатия

k_b – константа Больцмана

K₀, K_t , – отсчетная, актуальная и промежуточная (разгруженная из K_t) конфигурации

– собственно ортогональная группа

– n ‑ мерное евклидово пространство

– длина дуги траектории деформации (пластической деформации)

t – время (или его аналог)

Т_г – гомологическая температура

Х – обозначение материальной частицы в материальном способе описания движения

– лагранжевы координаты в декартовой ортонормированной и произвольной криволинейной системах координат, соответственно

– средняя деформация

– интенсивность деформаций

Н – функция Хэвисайда, Н(х)=0 при х0 и Н(х)=1 при х0

η – вязкость материала

– коэффициент Пуассона

 — температура

– среднее напряжение

– интенсивность напряжений

– предел пропорциональности

– предел текучести

– предел прочности

– интенсивность сдвиговых напряжений

, ^* — системы отсчета, отличающиеся жестким движением

b , b – вектор Бюргерса и его модуль

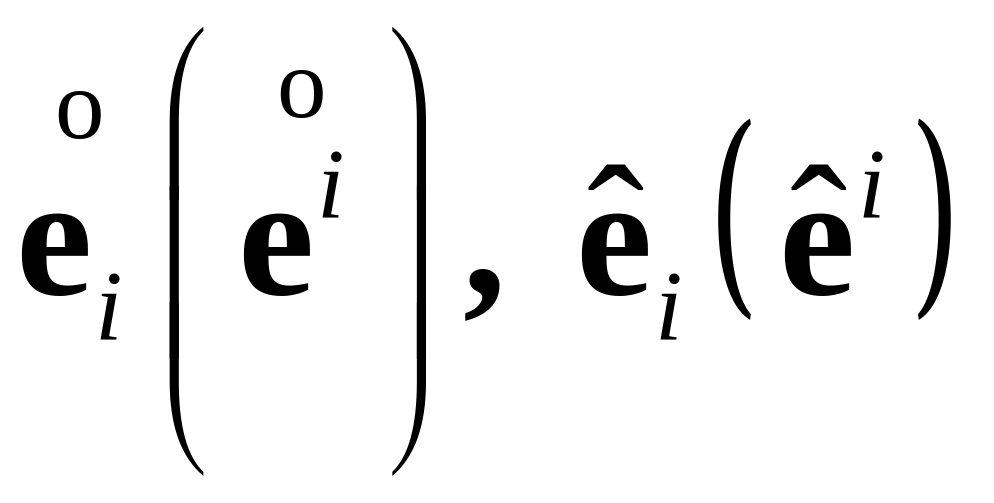– лагранжевы векторы основного (сопряженного) базиса в K₀ и K_t

R₀, r – радиус-векторы частиц в K₀ и K_t

– набла – операторы (операторы Гамильтона) в отсчетной и актуальной конфигурациях

D, d — тензор деформации скорости на макро- и мезоуровне

Е (или g) – единичный (метрический) тензор

() — определяющее отображение

, C — мера и тензор деформации Коши-Грина

— тензорзначные внутренние переменные

– «явные» и «скрытые» внутренние переменные

– ориентационный тензор k-й кристаллографической системы, его симметричная и антисимметричная составляющие

O(t) – собственно ортогональный тензор

– параметры воздействия

R – ортогональный тензор, сопровождающий деформацию

– операторы конститутивных соотношений

U, V – левый и правый тензоры искажения

– тензор малых деформаций и его девиатор

Π ( ) – тензор (4-го ранга) упругих характеристик макроуровня (мезоуровня)

– тензор остаточных микронапряжений

,  (S, s) – тензор напряжений Коши макро- и мезоуровня (их девиаторы)

– тензорзначные функции, характеризующие нетермомеханические воздействия на материал

– градиент места

Є – тензор Леви–Чивита

, – индексы, относящиеся к упругим и пластическим составляющим

– обозначение объективной производной

 – скобки Мак-Кэйли, х=0 при х0 и х=х при х0

– осредненные величины

Сокращения

ГНД – геометрически необходимые дислокации

ГЦК, ГПУ, ОЦК – гранецентрированная кубическая, гексагональная плотноупакованная, объемно-центрированная кубическая (кристаллические решетки)

ДОН – дислокации ориентационного несоответствия

ДУ – дефект упаковки

ЗГС – зернограничное скольжение

ЗУ – замыкающие уравнения

ИПД – интенсивное пластическое деформирование

КлК – классические континуумы

КСК – кристаллографическая система координат

МДТТ – механика деформируемого твердого тела

МСС – механика сплошной среды

ОК – обобщенный континуум

ОС – определяющие соотношения

ПО – представительный объем

СНД – статистически накопленные дислокации

СП – сверхпластичность

СПД – сверхпластическое деформирование

СС – система скольжения

СТТ – стандартный тетраэдр Томпсона

ТОС – теория определяющих соотношений

ФРО – функция распределения ориентаций

ФТП – физическая теория пластичности

ФТТ – физика твердого тела

ЭДУ – энергия дефекта упаковки

ЭУ – эволюционные уравнения