Вопросы к главе 3

1. Выведите уравнение Орована.

2. Перечислите кристаллографические системы, по которым осуществляется движение краевых дислокаций в ГЦК и ОЦК кристаллах.

3. По каким системам реализуется сдвиг и двойникование в ГПУ–кристаллах?

4. Что называется неконсервативным движением дислокаций и за счет каких механизмов оно реализуется?

5. Приведите соотношение для тензора деформации скорости при произвольном движении краевых и винтовых дислокаций, проверьте его выполнение для скольжения и переползания одиночных дислокаций.

6. Приведите кинематические соотношения, определяющие деформирование при двойниковании.

7. Дайте определения статистически накопленных и геометрически необходимых дислокаций. Каковы физические механизмы их формирования? С помощью каких моделей они вводятся в описание неупругого деформирования?

8. Опишите физические причины возникновения поворотов кристаллической решетки?

9. Опишите модель поворота Тейлора.

10. Приведите соотношения для описания «материального поворота», сопоставьте их с уравнениям модели поворота Тейлора.

Глава 4. Жесткопластические модели

4.1. Модель Закса

Одной из первых попыток построения одномерной модели поликристалла на основе рассмотрения совокупности монокристаллов была модель Закса [133? 158]. В данной модели зерна полагались ориентированными хаотически (по равномерному закону), взаимодействием между зернами пренебрегалось (в силу чего эту модель можно назвать «полностью несовместной», как по деформациям, так и по напряжениям). Модель Закса в исходной формулировке предназначена только для определения предела текучести при одноосном растяжении поликристаллического образца по известному значению критического напряжения сдвига в системах скольжения (СС) кристаллитов (зерен) и заданному закону распределения ориентаций кристаллографических систем координат (КСК) зерен по отношению к лабораторной системе координат (ЛСК).

Рассмотрим одноосное нагружение цилиндрического образца из поликристаллического материала; ось х₁ с единичным вектором базиса е₁ направим вдоль оси образца. В рассматриваемом случае все компоненты тензора напряжений Коши за исключением полагаются нулевыми. Мысленно пересечем образец плоскостью, перпендикулярной его оси, и выделим все зерна, пересекаемые данным сечением (см. рис.4.1.1). В модели Закса полагается, что каждое из зерен также находится в состоянии однородного одноосного растяжения (сжатия), как и образец в целом, однако величины напряжений в каждом зерне могут отличаться от напряжений в других зернах.

Принимается, что достижению предела текучести образца в целом соответствует активизации хотя бы одной СС в каждом зерне сечения. Величина напряжений в каждом зерне определяется из условия достижения касательным напряжением в наиболее благоприятно ориентированной СС («слабейшем звене») величины критического напряжения сдвига , считающейся известной для анализируемого типа кристаллитов и одинаковой для всех зерен. Таким образом, для каждого из зерен, попавших на введенное сечение, зная ориентацию КСК относительно ЛСК, вначале определяется фактор Шмида 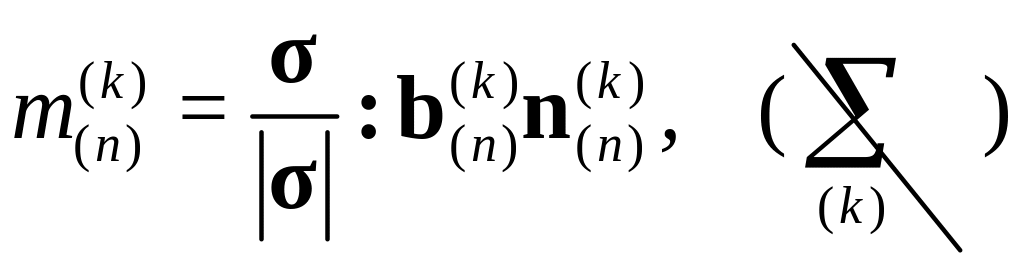для каждой из СС данного зерна (для рассматриваемого случая одноосного нагружения ), где п – номер зерна, после чего устанавливается его максимальное значение. Далее для каждого п-го зерна напряжение определяется как

Рис. 4.1.1. Схема к модели Закса

Обозначив через S_(n) площадь поперечного сечения n –го зерна, пересекаемого введенным сечением, а через S – площадь поперечного сечения образца в целом, предел текучести при одноосном нагружении определяется тогда соотношением:

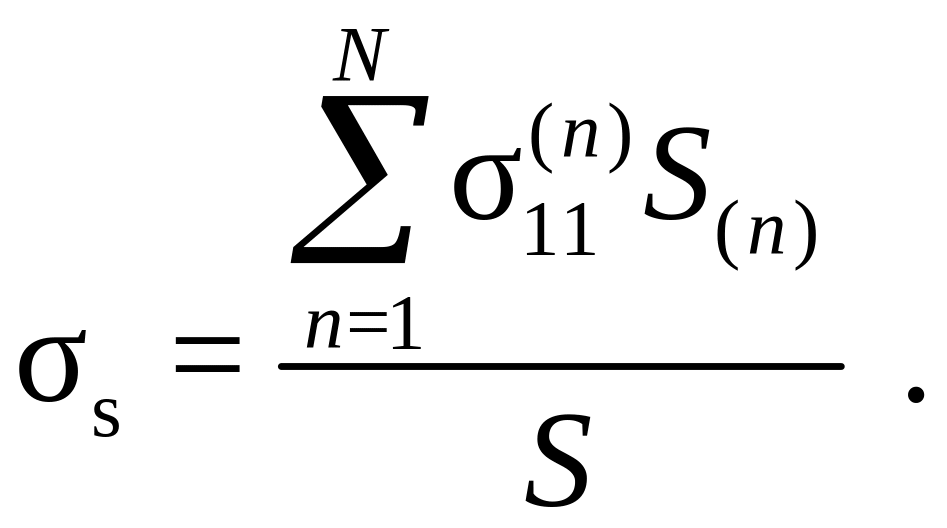
Расчеты по модели Закса дают значение макроскопического напряжения текучести , равное 2,2_c. Хотя полученный результат существенно (примерно на 30%) отличается от экспериментально определенного предела текучести, его все же следует признать удовлетворительным для своего времени.

К основным недостаткам модели Закса относятся невыполнение условий равновесия и совместности деформаций соседних зерен, неучет упругих деформаций; указанные недостатки отмечаются во многих работах (например, [119], где приведен и краткий обзор ранних работ по физическим теориям пластичности). Модель Закса может быть использована для определения предела текучести при одноосном нагружении, для построения кривой - требуются дополнительные предположения.