3.4 Ротационные моды деформирования, модели ротации

В работах В.Е.Панина, В.В.Рыбина указывается, что существенную роль

в инициации поворотов решетки играет несовместность скольжения дислокаций в соседних зернах. Действительно, в реальном поликристалле происходит достаточно сложный процесс: при больших деформациях появляются субзерна, фрагменты, которые начинают разворачиваться, начиная от границ с соседними зернами. Активируется так называемая ротационная мода пластичности [34]: «Вследствие несовместности пластической деформации в граничащих зернах возникают внутренние напряжения, активизирующие новые (аккомодационные) СС. В стыках фасеток зерен возникают разориентировки участков зерна, примыкающих к разным фасеткам (т.е. возникает стыковая дисклинация). Далее стыковая дисклинация распространяется в тело зерна, т.е. превращается в обычную дисклинацию, образующую новую границу разориентации (границу фрагмента). С этой границей вновь взаимодействуют решеточные дислокации, вновь образуются стыковые дисклинации, и т.д. Таким образом, процесс фрагментации начинается с границ зерен и постепенно распространяется вглубь зерен».

Разумеется, детальное описание столь сложной физики процесса на настоящем этапе вряд ли возможно, т.к. требуется введение еще одного масштабного уровня, внутренних переменных на нем, эволюционных уравнений для внутренних переменных на основе анализа действующих механизмов. Как правило, в многоуровневых моделях в рамках принятого ограничения иерархии масштабных уровней повороты решетки описываются интегрально по зернам (по существу, при больших деформациях под зернами надо понимать «эффективные» зерна со средними по объему зерна характеристиками), однако предпринимается попытка более детального учета физики процесса. С этой целью поворот решетки (эволюция ортогонального тензора, связывающего КСК и ЛСК) представляется суммой двух составляющих: поворота решетки зерна в предположении его изолированности (далее это поворот называется «материальным», который определяется ортогональным тензором, сопровождающим упругую деформацию) и поворота только решетки зерна при сохранении конфигурации зерен в физическом пространстве («решеточной» поворот), движущая сила этого поворота – несовместность движения дислокаций в соседних зернах.

Модели ротации решетки

Наиболее популярными моделями поворота решетки являются модель стесненного поворота Тейлора, определяющая спин решетки как разность тензора вихря и антисимметричной части тензора пластических сдвигов, и модель, связывающая поворот решетки с материальным поворотом, определяемым ортогональным тензором, сопровождающим упругую деформацию.

Стесненный поворот по Тейлору

Согласно модели стесненного поворота Тейлора в современной интерпретации [178] градиент скорости перемещений на мезоуровне (уровне зерна) представляется в виде:

,

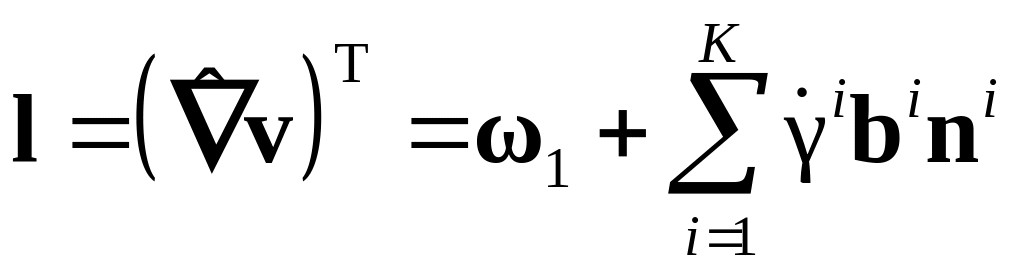где – оператор Гамильтона, определенный в актуальной конфигурации, – антисимметричный тензор спина решетки зерна, остальные величины определены выше. Соотношение предполагает для связи моделей мезо- и макроуровней (вместо первоначально используемой самим Тейлором [164] гипотезы однородности деформаций (гипотезы Фойгта)) использование «расширенной» гипотезы Фойгта, устанавливающей однородность градиентов скоростей перемещений . В силу того, что в рамках этой гипотезы материал полагается «стесненным» (деформации зерен ограничены соседями), модель Тейлора часто называют «полностью стесненной».

С учетом из соотношения тензор спина решетки зерна можно выразить следующим образом:

.

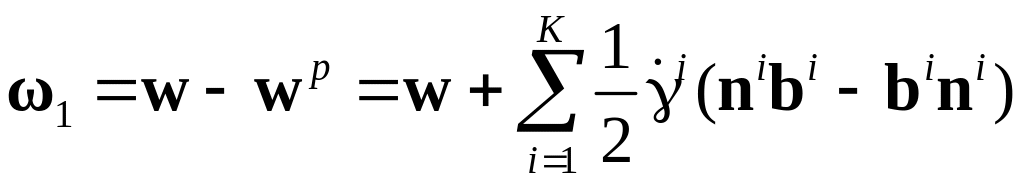где w – тензор вихря, .

Отметим, что первоначально модель поворота решетки Тейлора была предложена для жесткопластической модели внутризеренного деформирования, поэтому анализ логично провести для такой модели. Тогда при отсутствии скольжения дислокаций деформирование отсутствует, вращение решетки зерна согласно описывается тензором вихря – зерно вращается как жесткое тело, что соответствует представлению движения согласно теореме Коши–Гельмгольца [31].

Модель «материального» поворота

Другим популярным для описания поворотов решетки является следующий подход: для описания кинематики используется мультипликативное разложение Ли градиента места, поворот решетки связывается с материальным поворотом, который определяется ортогональным тензором , сопровождающим упругую деформацию.

Отметим, что при использовании данной модели, как и при использовании модели стесненного поворота Тейлора, принимается «расширенная» гипотеза Фойгта, предполагающая однородность градиентов деформации (градиентов скоростей перемещений ).

Градиент деформации F (транспонированный градиент места), линейно связывающий материальные отрезки в отсчетной К₀ и в текущей К_t конфигурациях ( ) представляется мультипликативным разложением упругой и пластической составляющих градиента деформации [31]:

,

где – радиус-векторы частицы в отсчетной К₀, актуальной К_t и промежуточной (разгруженной) К_x конфигурациях (последняя получается из текущей разгрузкой до достижения нулевых напряжений), – оператор Гамильтона, определенный в К_x; аналогичные соотношения справедливы на мезоуровне.

Упругая составляющая градиента деформации мезоуровня представляется в виде полярного разложения

.

Материальный поворот связывают с ортогональным тензором , сопровождающим упругую деформацию (называемым также тензором ротации). Пластическая составляющая градиента деформации определяется соотношением:

,

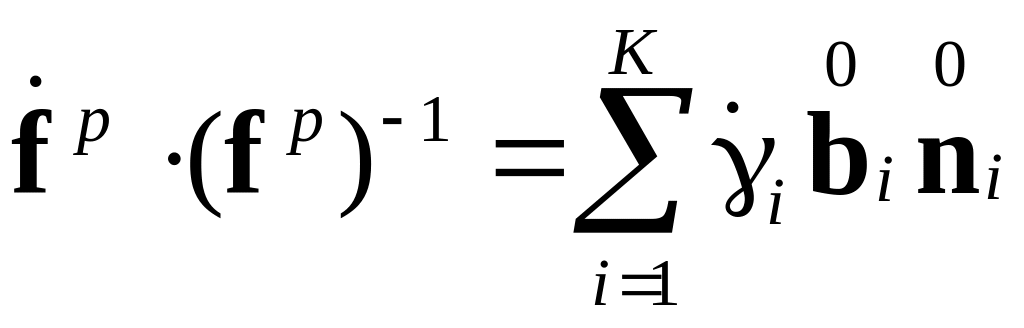где векторы – единичные векторы в направлении вектора Бюргерса (направления сдвига) и нормали для системы скольжения, определенные в отсчетной конфигурации.

Таким образом, в результате воздействия (деформирования) произвольное зерно с некоторой ориентацией испытывает пластические сдвиги (без изменения ориентации решетки), упругие искажения и повороты; с последними связывается квазитвердое движение (конечные повороты как жесткого целого [31]), которое, в свою очередь, в рамках рассматриваемой модели и описывает поворот решетки зерна.

Сравнение моделей ротации решетки

Для сравнения (с математической точки зрения) вышеприведенных моделей поворота решетки, необходимо для модели «материального» поворота определить спин решетки .

Используя разложение , полярное разложение , малость упругих деформаций можно показать, что тензор спина решетки при квазистатическом нагружении определяется согласно [57]:

,

где , , ,

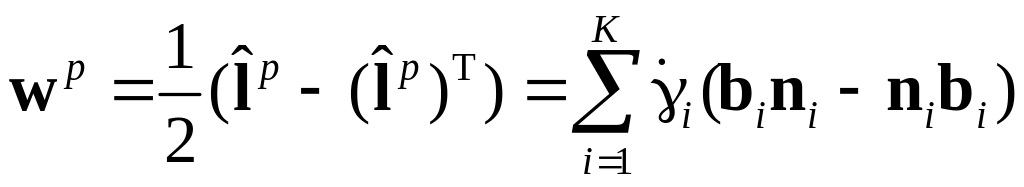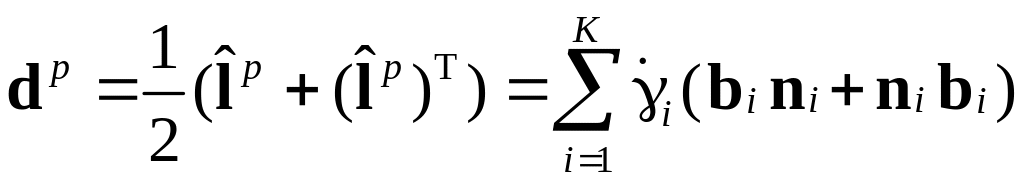– тензор четвертого ранга упругой податливости.

Учитывая, что согласно модели стесненного поворота Тейлора спин решетки есть , получаем связь спинов решетки для моделей:

.

Таким образом, при квазистатическом деформировании рассмотренные модели поворотов решетки в силу малости упругих деформаций будут давать незначительно отличающиеся результаты.

Существующие в настоящее время ФТП можно разделить на три широких класса: жесткопластические модели, упругопластические модели и (упруго) вязкопластические модели [45-48]. Ниже остановимся на каждом из этих классов отдельно.