3.2. Моды неупругого деформирования монокристаллов

Скольжение

Основным механизмом неупругого деформирования монокристаллов в физических теориях пластичности считается движение краевых дислокаций. Конечно, наряду с краевыми дислокациями в реальных моно- и поликристаллических телах наличествуют и винтовые дислокации, и множество других дефектов. То, что именно движущиеся дислокации являются основным источником появления необратимых деформаций – факт, подтвержденный огромным количеством экспериментов. Включение в рассмотрение только краевых дислокаций обусловлено отчасти сложившейся в ФТП традицией; кроме того, как известно [27], винтовые дислокации имеют бόльшую энергию активации и меньшую плотность по сравнению с краевыми дислокациями.

В кристаллических телах плоскости залегания и ориентация векторов Бюргерса, вдоль которых осуществляется трансляционное движение (скольжение) краевых дислокаций, известны; ими являются наиболее плотно упакованные плоскости и направления. Так, в ГЦК – металлах скольжение краевых дислокаций осуществляется в плоскостях системы 111 по направлениям 110, соединяющим ближайшие в плоскости наиплотнейшей упаковки атомы (иначе говоря, в системе скольжения {111}, <110>), итого – 12 систем скольжения (СС). При повышенных температурах в некоторых ГЦК кристаллах (например, в алюминии) наблюдается скольжение по трем плоскостям системы {100} по двум направлениям <110>. В ОЦК – решетке трансляционное движение краевых дислокаций осуществляется в плоскостях {110}, {112} или {123} по направлениям <111>; каждому из 4-х направлений <111> соответствуют по три плоскости скольжения из систем плоскостей {110}, {112} и шесть плоскостей скольжения из системы {123}, так что полное число СС достигает 48 (см. рис. 3.2.1-3.2.4). В ГПУ металлах скольжение имеет место по базисным плоскостям {0001} в направлении , плоскости по направлению ; возможно также скольжение в так называемых призматических плоскостях (см. рис. 3.2.5). Обозначив через а длину ребра кубической решетки, нетрудно установить, что векторы Бюргерса в ГЦК решетки суть векторы а/2<110> (модуль вектора Бюргерса ), в ОЦК – а/2 <111> (модуль – ), в ГПУ – (модуль – а; для ГПУ а – длина стороны правильного шестиугольника в базисной плоскости). Полный перечень систем скольжения ля ГПУ–кристаллов приведен в таблице 3.2.1, в которую включены также системы двойникования (СД).

Таблица 3.2.1

Системы скольжения (СС) и двойникования (СД) ГПУ — кристаллов

Механизм деформации	Плоскость	Направление	Количество систем
Базисное скольжение			3
Призматическое скольжение			3
Пирамидальное скольжение			12
Двойники сжатия			6
Двойники растяжения			6

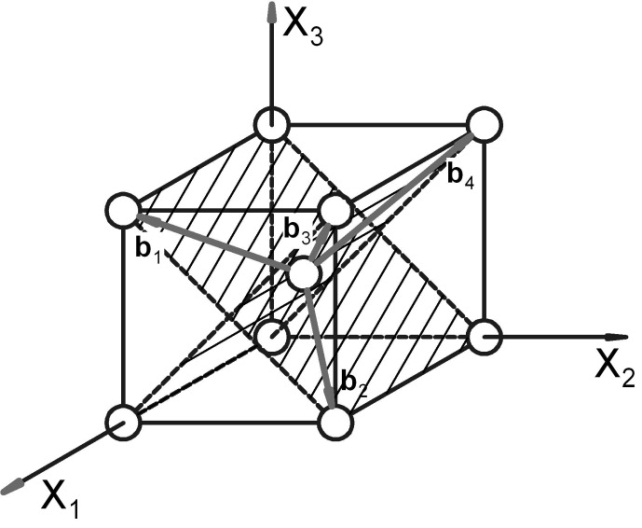
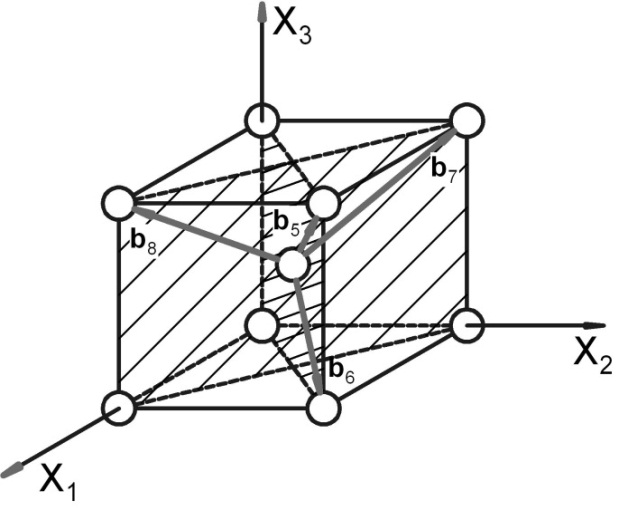
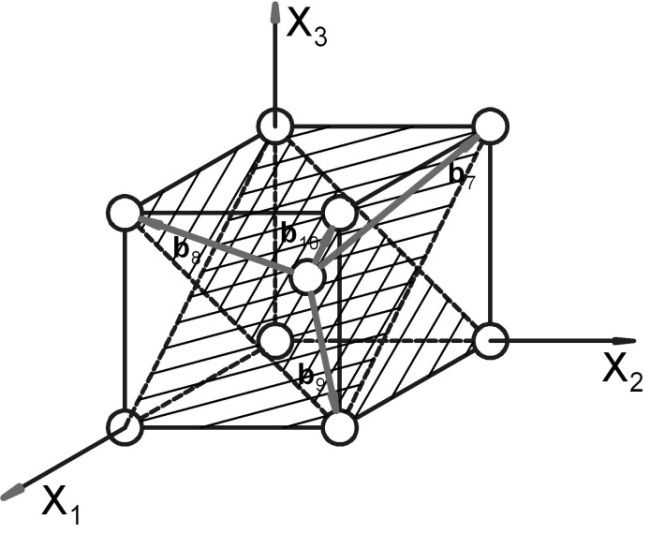
Рис. 3.2.1. Система плоскостей скольжения {110} и соответствующие им направления <111> (ОЦК‑решетка)

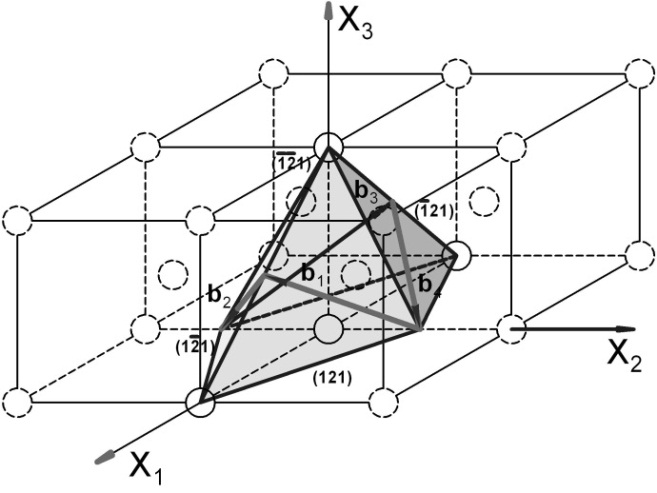
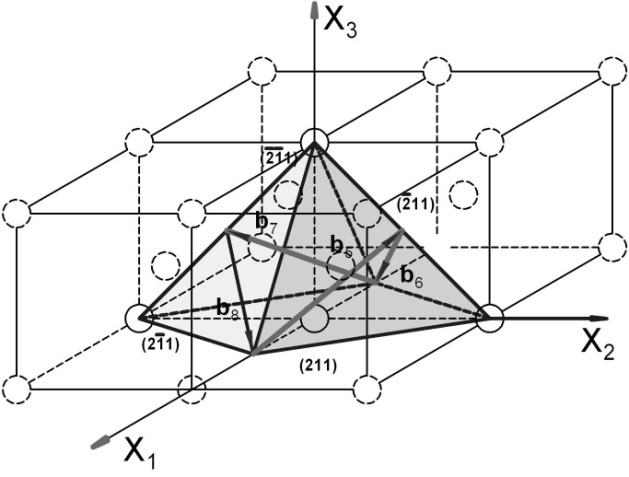
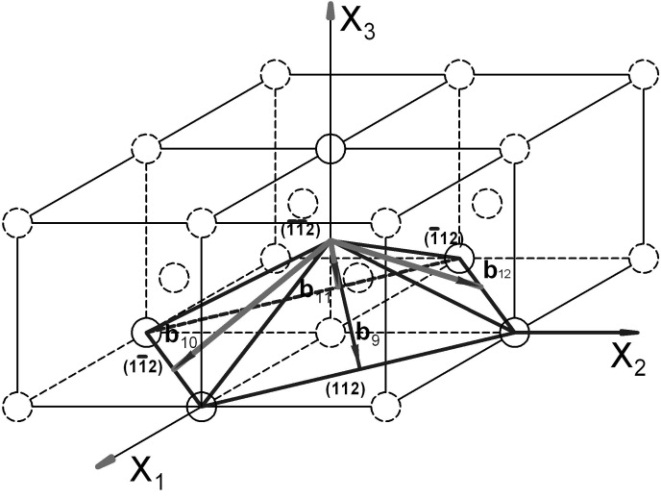
Рис. 3.2.2. Система плоскостей скольжения {112} и соответствующие им направления <111> (ОЦК‑решетка)

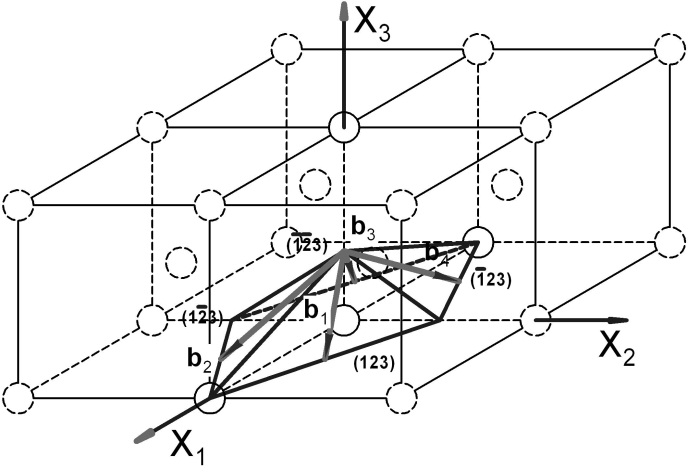
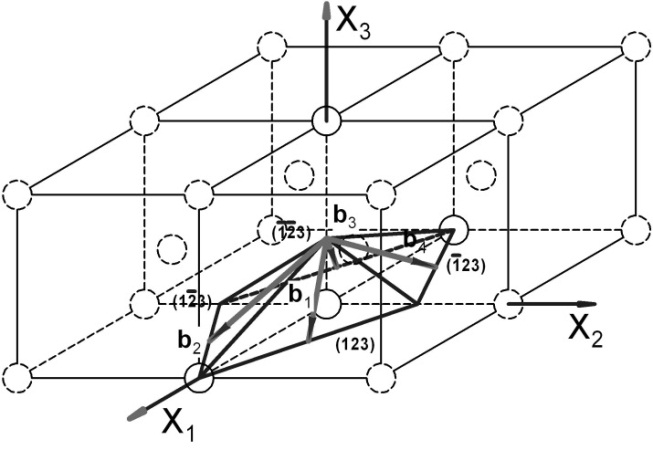
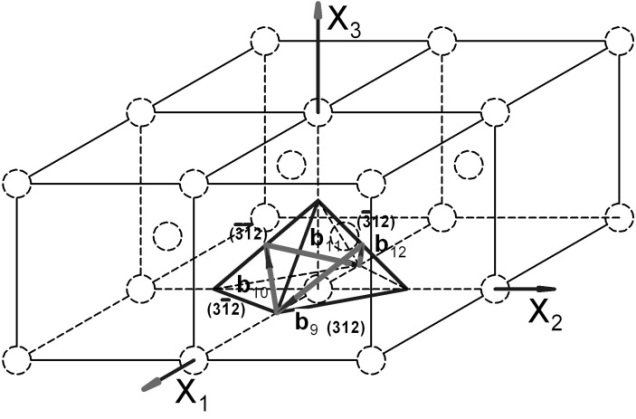
Рис. 3.2.3. Система плоскостей скольжения {123} и соответствующие им направления <111> (ОЦК‑решетка)

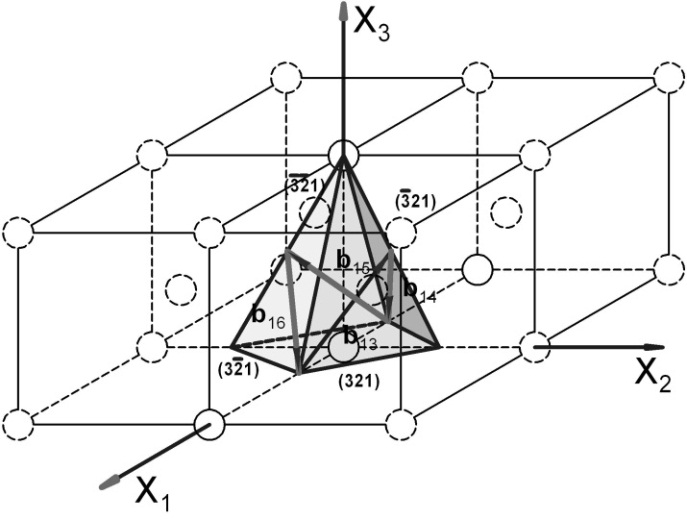
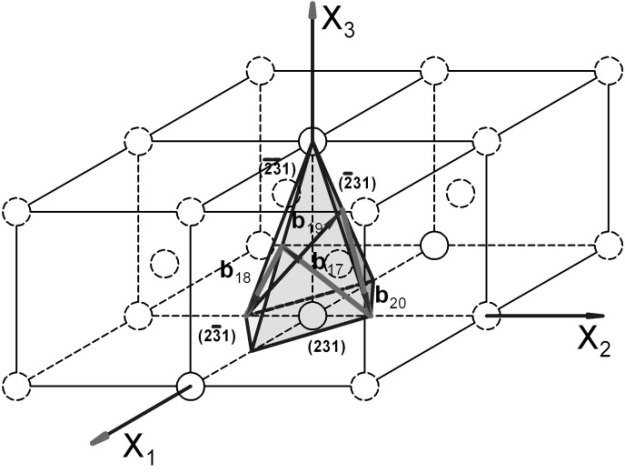
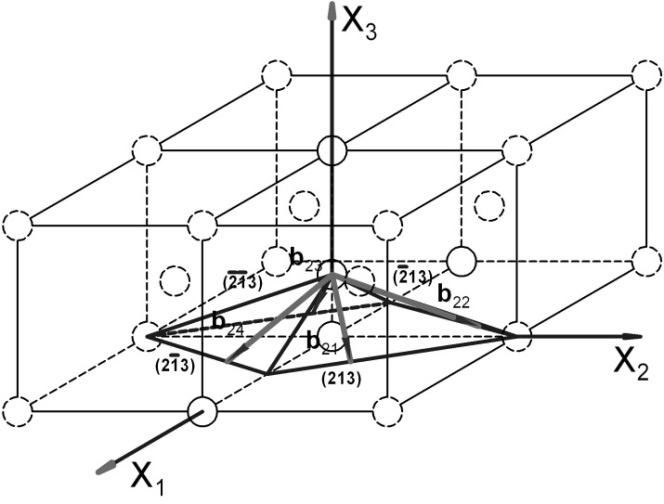
Рис. 3.2.4. Система плоскостей скольжения {123} и соответствующие им направления <111> (ОЦК‑решетка)

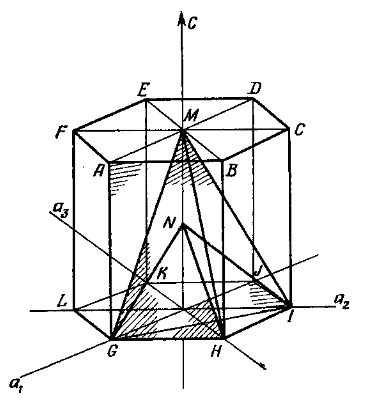
Рис. 3.2.5. Кристаллографические плоскости в ГПУ-структуре [56]: GHIJKL – базисная плоскость , ABHG – призматическая плоскость , GHM – пирамидальная плоскость , GHN – пирамидальная плоскость , GIM – пирамидальная плоскость , GIN – пирамидальная плоскость

Напомним, что условием активации k-й СС является достижение касательного напряжения в ней некоторого критического напряжения :

где – ориентационный тензор k-ой системы скольжения; чаще в литературе в качестве ориентационного тензора k-ой системы используется симметричная часть диадного произведения:

.

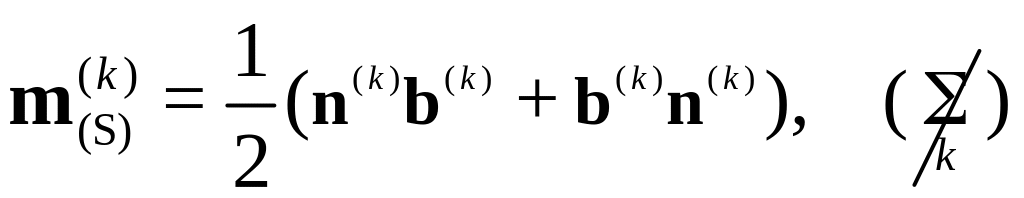Нетрудно видеть, что ориентационный тензор является девиатором.

Следует отметить, что замена диады на симметризованный ориентационный тензор не имеет корректного физического обоснования. Действительно, такая замена означает, что при активизации реально существующей в кристалле k-ой СС активируется также другая СС с нормалью и направлением скольжения , которая в реальном кристалле может отсутствовать, в чем нетрудно убедиться, например, для ГЦК кристаллов. Тем не менее, в известных авторам работах симметризация используется всегда. Как представляется, данное обстоятельство связано с трудностями применения несимметричных мер деформированного и напряженного состояния, прежде всего – с отсутствием экспериментальных данных о (несимметричных) компонентах тензора упругих характеристик. Заметим, что в некоторых работах указанная симметризация осуществляется неявным образом, т.е. в законе Шмида и выражении неупругой составляющей тензора деформации скорости применяется несимметричный ориентационный тензор, но затем используется симметричный (по индексам первой и второй пар) тензор упругих характеристик с в законе Гука.

Условие , как отмечено выше, обычно называется законом Шмида, устанавливающим момент начала неупругого деформирования при достижении в системе скольжения критического значения касательного напряжения. При реализации в одной системе скольжения говорят об одиночном скольжении; если кристалл подвергается нагружению, при котором дислокации начинают скользить в двух или более системах, то говорят о двойном или множественном скольжении. При наличии К активных систем скольжения (т.е. СС, для которых удовлетворяется закон Шмида ) в произвольный момент деформирования девиатор пластической составляющей тензора деформации скорости определяется соотношением:

, ,

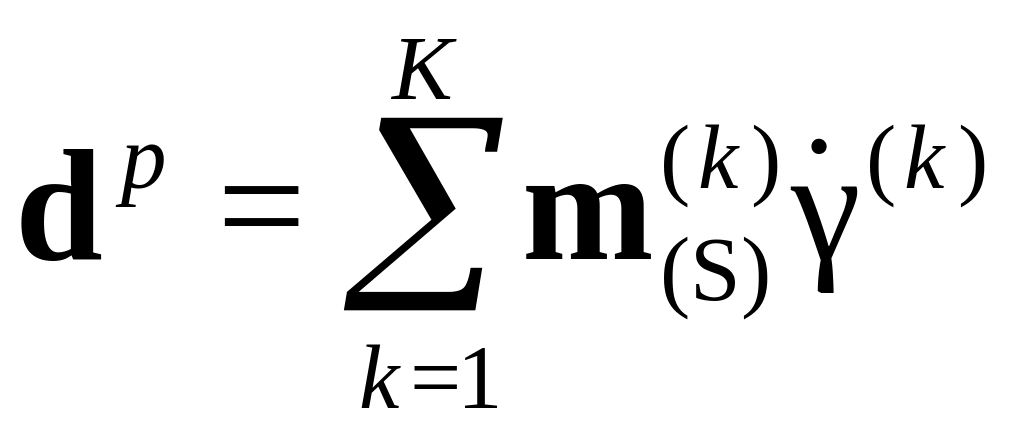где – скорость сдвига в k-ой СС.

Переползание

Как было отмечено выше, краевые дислокации могут испытывать локальные смещения в плоскости скольжения в направлении вектора Бюргерса, такое движения называется скольжением (или – консервативным движением) краевых дислокаций. Однако, возможно смещение дислокации перпендикулярно вектору Бюргерса в соседнюю плоскость скольжения. При таком движении необходимо устранить ряд атомов, образующих край экстраплоскости. Это может произойти путем диффузии этих атомов в междоузлия или вакансий на эти места [56]. Такой процесс получил название переползания (неконсервативного движения) дислокаций и его осуществление в значительной степени обусловлено термической активацией.

Заметим, что в случае винтовой дислокации «лишней» полуплоскости атомов нет, поэтому она может свободно скользить по любой плоскости, которая содержит линию дислокации и вектор Бюргерса.

В общем случае скольжения и переползания краевых и движения винтовых дислокаций выражения для девиатора деформаций скорости имеет вид [30]:

,

где – тензор (третьего ранга) Леви–Чивита,

N – тензор третьего ранга, определяемый соотношением:

.

В последнем соотношении f(b, l, r) – функция распределения дислокаций в точке r по параметрам b и l, где l – единичный вектор, направленный вдоль линии дислокации (для винтовой дислокации совпадает с направлением вектора Бюргерса; для краевой дислокации векторы l, b, n составляют правую тройку), v – скорость движения дислокации.

Двойникование

Другим механизмом неупругого деформирования является двойникование. Отметим, что двойникование может не вносить большого вклада в неупругую деформацию, но играет весьма важную роль в процессе скольжения краевых дислокаций – основного механизма неупругого деформирования. Процесс двойникования будет рассматриваться подобно скольжению краевых дислокаций. Используя две конфигурации кристаллита: отсчетную конфигурацию (монокристалл находится в недеформированном состоянии, двойники отсутствуют) и актуальную (в монокристалле появляются несколько двойниковых прослоек), можно показать, что осредненный (по кристаллиту) градиент места, описывающий формоизменение двойникованием, имеет следующий вид:

,

где E – единичный тензор; b_tw – направление сдвига двойника; n_tw – нормаль к плоскости двойникования; f – безразмерная величина, равная отношению объемов двойниковых прослоек, в которых произошел сдвиг, к объему всего кристаллита (объемная доля двойников); – величина постоянного сдвига двойника.

Полагая, что двойникование происходит непрерывно, существует и конечно, осредненный градиент скорости перемещений двойникования для монокристалла в разгруженной конфигурации можно записать в виде [142]:

.

Таким образом, двойникование может рассматриваться как «псевдоскольжение» со скоростью «двойникового» сдвига и ориентационным тензором . Для каждой k-ой системы двойникования введем обозначение симметричного ориентационного тензора t^(k) в актуальной конфигурации:

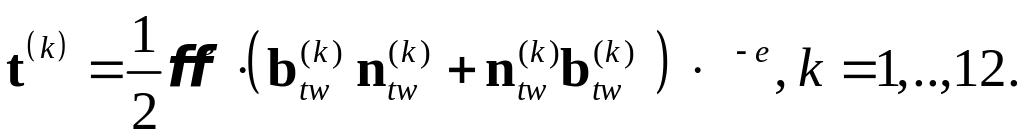
Неупругую составляющую тензора деформации скорости, связанную с двойникованием, можно записать в виде, аналогичном :

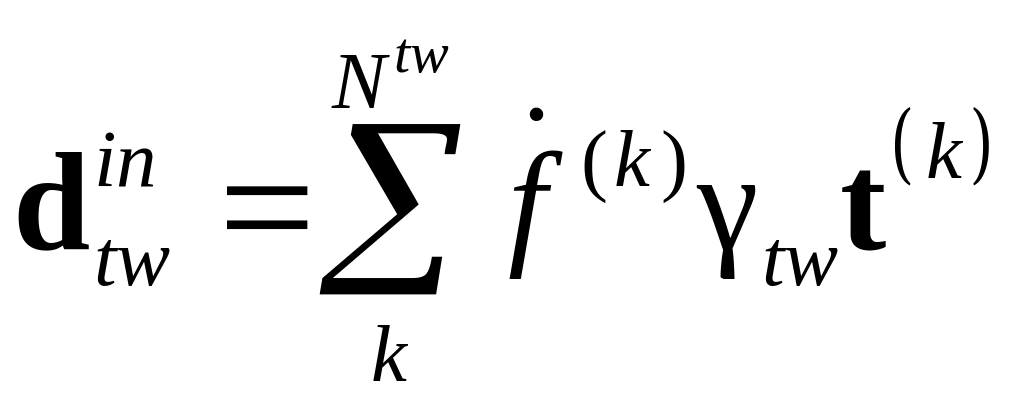
Условием активации k-ой системы двойникования является достижение касательного напряжения в ней некоторого критического напряжения , условие записывается в виде, аналогичном закону Шмида (3.1.1):

,

Приведенные соотношение позволяют включить двойникование в физические теории пластичности наряду с деформированием скольжением дислокаций.