2.3 Деформирование монокристалла двойникованием

Основным механизмом неупругого деформирования в физических теориях пластичности является движение краевых дислокаций, что подтверждено многочисленными экспериментами. Двойникование не является преобладающим видом неупругого деформирования в металлах с большим числом систем скольжения (ГЦК и ОЦК – кристаллы) и в основном происходит в металлах, в которых скольжение дислокаций по некоторым СС ограничено (ГПУ – кристаллы). Однако экспериментально установлено, что деформирование двойникованием происходит также в ОЦК и ГЦК металлах при низких гомологических температурах, в материалах с низкой энергией дефекта упаковки и при повышенных скоростях деформирования. Появление двойников приводит к значительному изменению отклика материала, поскольку двойники являются эффективным препятствием для движения краевых дислокаций. Поэтому для указанных классов кристаллов при моделировании упругопластического деформирования необходимо учитывать не только движение краевых дислокаций, но и двойникование, как механизм неупругого деформирования и как механизм упрочнения.

Двойник может быть образован посредством сдвига, иллюстрация такого типа двойникования показана на рис. 2.3.1 (заметим, что в физических теориях пластичности для описания двойникования обычно и используется представление деформирования за счет сдвига, величина которого фиксирована для каждого типа решетки, тогда сдвиговая деформация определяется объемной долей двойников). Для рассмотрения механического двойникования в металлах введем следующие общепринятые обозначения: K₁ – плоскость двойникования (габитусная плоскость), остающаяся неискаженной при двойниковании; η₁ – направление двойникового сдвига; K₂ – вторая неискаженная (инвариантная) плоскость; η₂ – направление, лежащее в плоскости K₂ и плоскости сдвига S, перпендикулярной плоскости двойникования K₁ и содержащей направление сдвига η₁

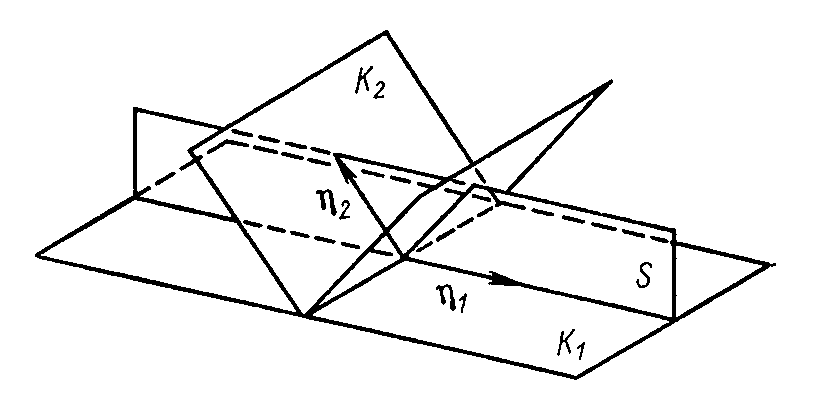
Рис. 2.3.1. Элементы двойникования

При двойниковании кристалла должны выполняться следующие критерии:

– две плоскости остаются неискаженными: плоскость двойникования K₁ и инвариантная плоскость K₂;

– инвариантная плоскость K₂ образует с плоскостью K₁ до и после двойникования одинаковые двугранные углы.

Рассмотрим кристаллогеометрию основных типов кристаллов – ГЦК, ОЦК и ГПУ. В случае правильной упаковки в ГЦК металлах последовательность атомных слоев имеет вид ABCABCABC… При двойниковании она меняется ABCABACBA… Двойниковый сдвиг, равный 0.707, происходит по направлениям <112> и плоскостям {111} (рис. 2.3.2). Перечислим элементы двойникования согласно введенным выше обозначениям:

Двойниковый переход удобнее всего наблюдать в сечении, перпендикулярном плоскости двойникования. На рис. 2.3.2 показан двойниковый сдвиг в направлении , создающий противоположную последовательность упаковки слоев по сравнению с первоначальной, так что решетка двойника является зеркальным отражением основной матрицы.

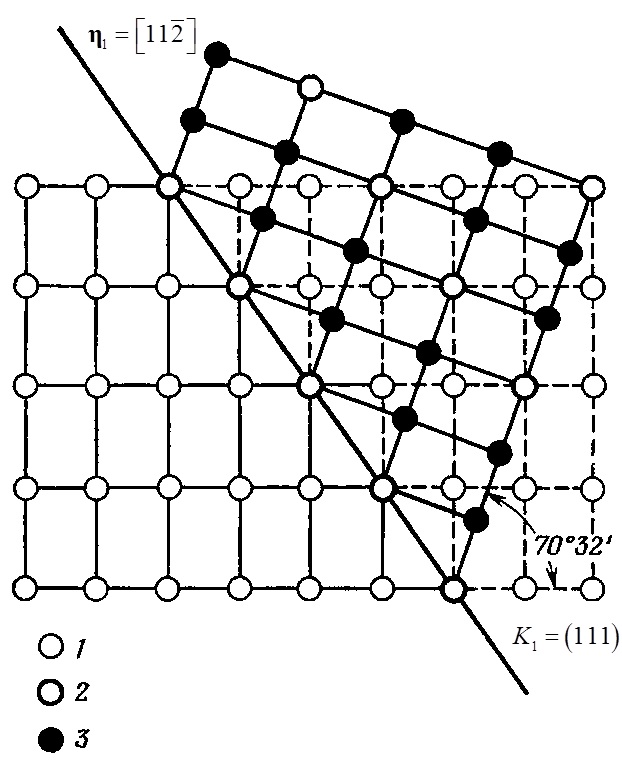
Рис. 2.3.2. Геометрия двойникования в ГЦК решетке. 1– положения атомов до двойникования, 2 – положения совпадающих атомов, 3 – двойниковые положения атомов

В ОЦК решетках плоскости упакованы в последовательности ABCDEFABCDEF и если в этой структуре задать смещение в направлении , то образуется дефект упаковки ABCDEFEFABCD… Для образования двойникового кристалла указанную операцию необходимо проделать на каждой последующей плоскости двойникования, чтобы получить последовательность упаковки ABCDEFEFDCBA. Индексы двойникования ОЦК структур имеют вид:

Величина двойникового сдвига равна 0,707. Двойник схематически изображен на рис. 2.3.3.

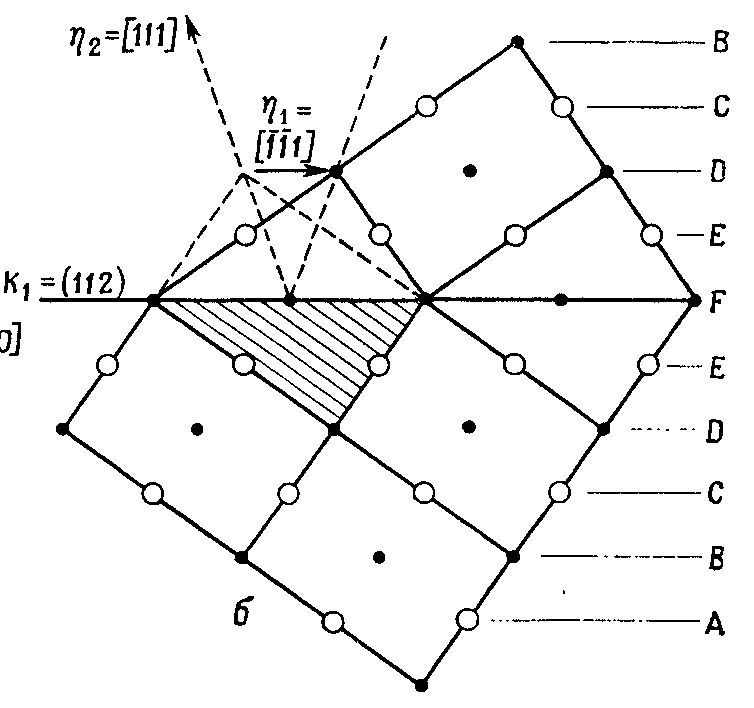
Рис. 2.3.3. Геометрия двойникования в ОЦК решетке. Темными точками обозначены атомы в плоскости чертежа, светлыми – выше или ниже плоскости чертежа

В ГПУ-кристаллах обнаружено достаточно много типов двойников, тип которых зависит от величины анизотропии кристалла c/a (а – длина стороны правильного шестиугольника в базисной плоскости, c – высота призмы), чем меньше это соотношение, тем больше способов двойникования [16]. Гексагональные кристаллы двойникуются по системам:

Величина и направление сдвига зависят от соотношения c/a, однако величина сдвига всегда являются относительно (кубических кристаллов) небольшой и изменяются в пределах от 0.175 (c/a=1.89, Cd) до 0.199 (c/a=1.59, Be). Следует заметить, что в данном случае описать движение атомов с помощью сдвига невозможно [16]. На рис. 2.3.4 изображена геометрия двойникования в ГПУ кристаллах, стрелками соединены начальные положения атомов до двойникования с ближайшими к ним атомами в двойнике (доказательства того, что атомы двигаются в процессе двойникования по этим путям, отсутствуют).

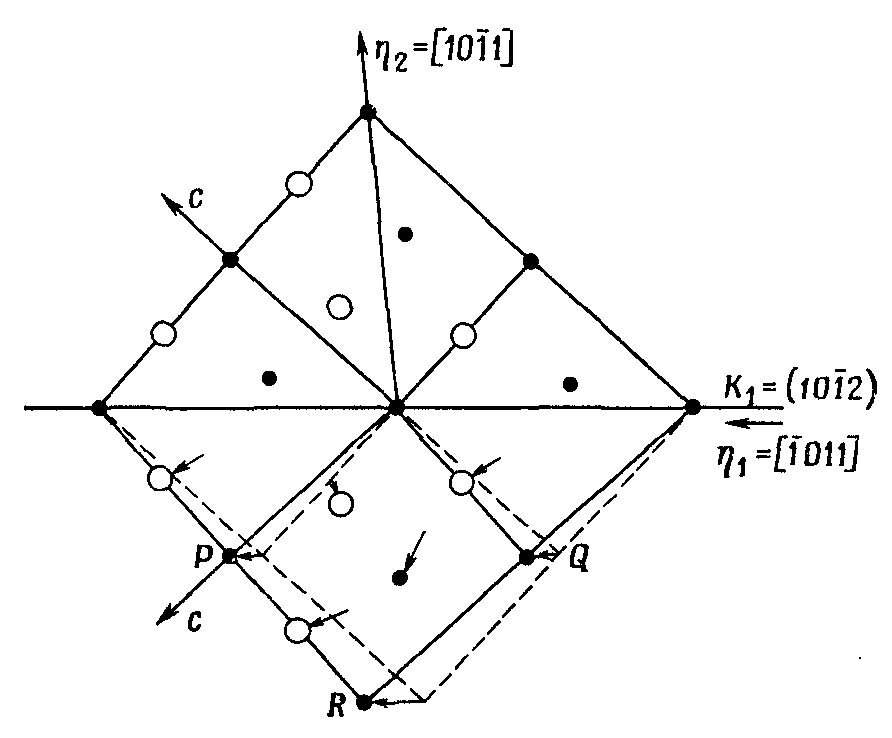
Рис. 2.3.4. Геометрия двойникования в ГПУ решетке. Темными точками обозначены атомы в плоскости чертежа, светлыми – выше или ниже плоскости чертежа

В литературе (например, [55, 56]) обсуждаются дислокационные механизмы, которые должны действовать в процессе двойникования. Важным классом таких дислокационных механизмов являются полюсные механизмы, которые впервые были предложены Котреллом и Билби для ОЦК и ГЦК металлов, а для ГПУ – Томпсоном и Миллардом [55]. Рассмотрим этот механизм на примере ОЦК кристалла. Краевая решеточная дислокация способна расщепляется по реакции [55]:

,

при которой изменение упругоей энергии в первом приближении равно нулю и согласно критерию Франка такая реакция возможна. Эта реакция может проходить при приложенных внешних напряжения и низкой энергии дефекта упаковки. Частичная дислокация (двойникующая) (направление η₁) способна скользить как в плоскости двойникования (плоскость K₁), так и в плоскости сдвига (плоскость S). При этом частичная дислокация закручивается вокруг полюсной дислокации , создавая спираль и дефект упаковки по последовательным плоскостям двойникования

Одним из важнейших параметров, определяющих зарождение и развитие двойников в кристалле, является энергия дефекта упаковки (ЭДУ). Напомним, что ЭДУ численно равна силе отталкивания частичных дислокаций и определяет ширину дефекта упаковки; чем ниже ЭДУ, тем больше ширина дефекта упаковки. В материалах с высокими значениями ЭДУ расщепленные дислокации практически отсутствуют (частичные дислокации «стягиваются» в полную). Отметим, что важнейшим этапом в образовании двойника, согласно приведенному выше механизму, являлось диссоциация полной дислокации на частичные. Вследствие этого в кристаллах с высокими значениями ЭДУ можно ожидать, что деформирование двойникованием затруднено и обеспечивается деформированием преимущественно за счет скольжения дислокаций. Напротив, низкие значения ЭДУ способствуют деформированию двойникованием. Влияние на двойникование также оказывает химический состав металлов (наличие примесей), так, например, добавка кремния к железу приводит к более активному протеканию двойникования при деформировании [56]. Можно сделать предположение, что примесные атомы приводят к уменьшению ЭДУ, следовательно, к более интенсивному деформированию двойникованием.

Необходимо также отметить влияние температуры на двойникование. Кристаллография сдвигов дислокаций зависит от температуры испытания [55], поэтому можно ожидать влияния температуры на развитие двойникования. Из экспериментов известно, что с понижением температуры склонность материала к двойникованию возрастает. Объяснение можно дать следующим образом: напряжение Пайерлса для полных дислокаций при понижении температуры нарастает быстрее, чем для частичных дислокаций, ответственных за двойникование, что приводит к затрудненности скольжения. Кроме того, с понижением температуры падает ЭДУ, что способствует деформированию двойникованием.

Наряду с температурными воздействиями существенное влияние на процесс двойникования оказывает скорость деформирования. Экспериментально установлено, что при деформировании со скоростями, меньшими некоторой критической скорости деформирования, двойникование в образцах не происходит. Существование минимальной скорости деформирования, при превышении которой имеет место двойникование, вероятно, можно объяснить тем, что повышение скорости деформации приводит к увеличению напряжения деформирования скольжением дислокаций, поэтому в кристалле при определенных скоростях деформации достигаются критические напряжения двойникования.