2.2 Взаимодействия дислокаций с дислокациями и точечными дефектами

Каждая из дислокаций обладает собственным полем напряжений. В силу быстрого затухания искажений кристаллической решетки при удалении от ядра дислокации для определения полей напряжений можно использовать линейную теорию упругости (следует учитывать, что вблизи ядра дислокации предпосылки линейной теории упругости малоприемлемы, поэтому полученным решением можно пользоваться только на определенном удалении от ядра, как правило – не менее 1.5–2 межатомных расстояний). Задача определения полей напряжений в этом предположении была решена Вольтерра еще в 1907 г. Для краевой дислокации при записи будем использовать две системы координат: декартову ортогональную Ох¹х²х³ (ось Ох³ направлена вдоль оси дислокации, ось Ох¹ – вдоль вектора Бюргерса, ось Ох² – вдоль нормали к плоскости скольжения) и цилиндрическую (r,z,θ), где ось z совпадает с Ох³, r – расстояние от оси дислокации, угол θ отсчитывается от плоскости скольжения. Тогда компоненты (в декартовой ортогональной системе координат) тензора собственных напряжений краевой дислокации определяются соотношениями [27, 32]:

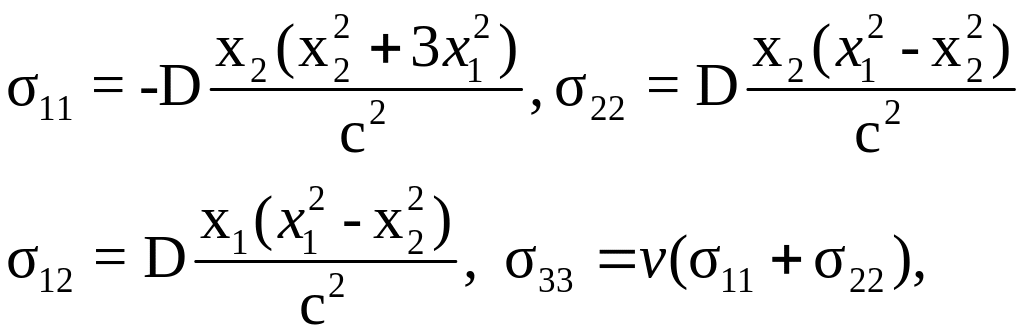
или в виде

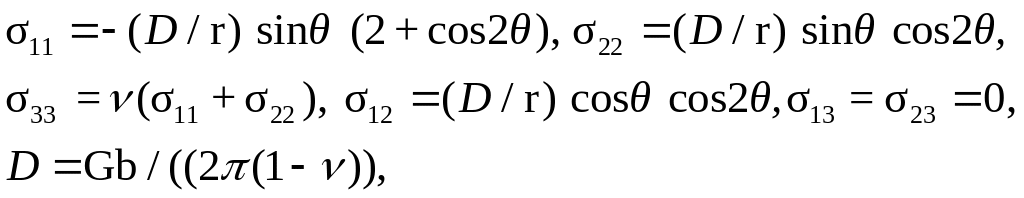
где с= , G – модуль сдвига, ν – коэффициент Пуассона.

Достаточно просто (по полю перемещений) получить компоненты тензора напряжений винтовой дислокации. Направим ось Ох³ вдоль оси дислокации, оси Ох¹ и Ох² расположены в перпендикулярной плоскости. Тогда компоненты тензора напряжений Коши в декартовой ортогональной системе координат равны:

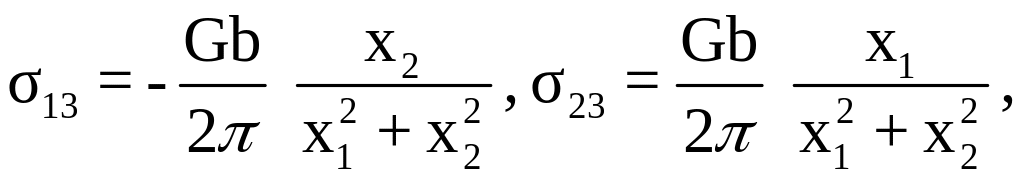
остальные компоненты равны нулю. Нетрудно видеть, что компоненты напряжений при удалении от ядра дислокации убывают обратно пропорционально расстоянию. При нагружении тела с дислокациями последние взаимодействуют собственными полями напряжений как с приложенными напряжениями, так и с полями напряжений других дислокаций (равно как и полями напряжений других типов дефектов); силы взаимодействия достаточно подробно рассматриваются во многих монографиях и учебных пособиях по ФТТ (например, [27, 32, 55]).

Следует отметить, что при приближении дислокации к свободной поверхности кристалла напряжение от дислокации и ее энергия падают, поскольку свободная поверхность не оказывает сопротивления движению дислокации. В силу этого дислокация притягивается к свободной поверхности; для математического описания этого явления используются фиктивные дислокации противоположного знака, расположенные соответствующим образом за свободной поверхностью (так называемые дислокации изображения), так что суммарное напряжение от двух дислокаций на свободной поверхности удовлетворяют тривиальным статическим граничным условиям. Заметим, что для моделирования данного эффекта при использовании соотношений макрофеноменологических теорий пластичности (например, теории пластического течения) для областей, примыкающих к границе образца, принимается пониженное значение напряжения течения.

Краевые дислокации, расположенные в перпендикулярных плоскостях, не взаимодействуют своими полями напряжений, в силу чего они могут как угодно близко подходить друг к другу и пересекаться. Рассмотрим две краевые дислокации с векторами Бюргерса b₁ и b₂, плоскости скольжения которых ортогональны. Первую дислокацию будем считать подвижной, вторую – неподвижной. При пересечении первой дислокацией второй происходит локальное перестроение в окрестности ядер дислокаций. При этом если вектор Бюргерса первой дислокации b₁ перпендикулярен вектору b₂, то на второй дислокации образуется ступенька краевой ориентации b₂ в направлении b₁ и величиной, равной модулю вектора b₁, первая дислокация при этом остается неизменной; ступенька представляет собой участок краевой дислокации. Если же векторы Бюргерса b₁ и b₂ параллельны друг другу, то при пересечении на каждой из дислокаций образуются так называемые перегибы, направление и величина которых равны вектору Бюргерса пересекающей дислокации; перегибы имеют винтовую ориентацию. Таким образом, пересечение дислокаций ведет к увеличению их длины, а следовательно – энергии упругих искажений решетки вблизи ядра дислокации; для продвижения прореагировавших дислокаций требуется повышенное значение напряжения, что позволяет говорить о деформационном упрочнении при пластическом деформировании. В то же время ступеньки и перегибы могут существенно облегчать соответственно процессы переползания и скольжения дислокаций при своем движении вдоль линий дислокаций. Связано это с тем, что потенциальный барьер для локального перемещения ступеньки и перегиба существенно меньше потенциального барьера соответственно переползания и консервативного перемещения дислокаций как целого; в силу этого и требуемые для перемещения ступеньки и перегиба напряжения значительно ниже значений критических напряжений для движения дислокаций как целого.

Дислокации взаимодействуют своими полями напряжений с другими дефектами, в том числе – с точечными. Как отмечалось в [51], такое взаимодействие является одной из возможных причин эффекта Портвена – Ле Шателье. Часть физиков связывает с этими взаимодействиями появление «зуба текучести» [51]. Используя введенную выше цилиндрическую систему координат, энергию П_тд взаимодействия краевой дислокации с примесным атомом (точечным дефектом) можно записать как [32]

,

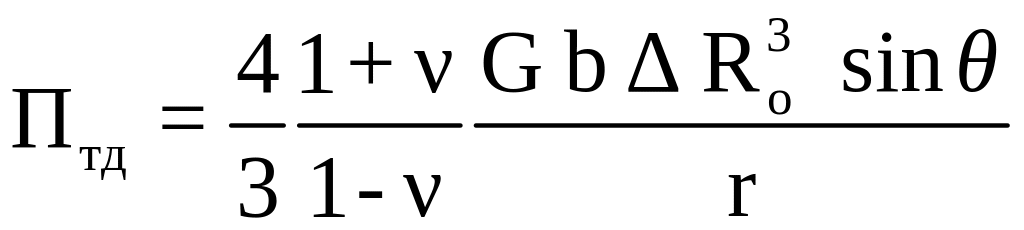где R_о – радиус атомов основного материала, 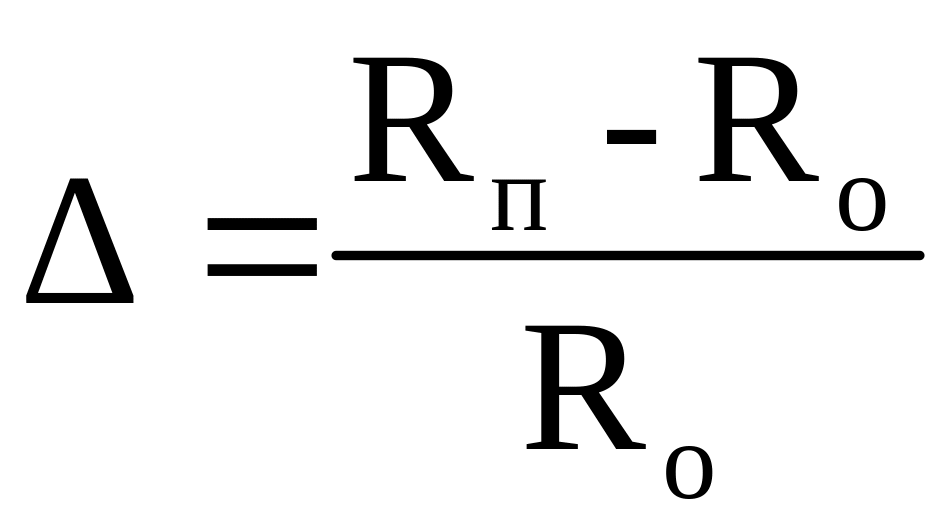, R_п – атомный радиус примеси. Силы взаимодействия определяются частными производными потенциальной энергии по координатам цилиндрической системы координат :

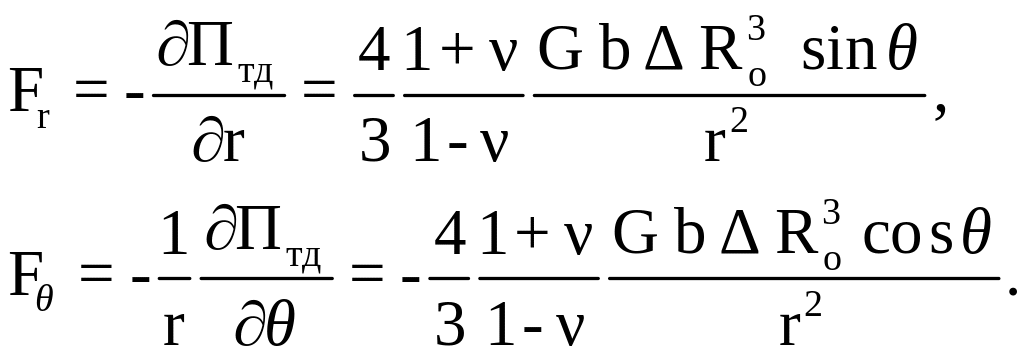
Приведенные соотношения, конечно, справедливы только в области выполнения принятых при их выводе гипотез и не могут напрямую использоваться при построении ОС на макроуровне. Однако в последние годы все большее распространение получают методы дислокационной динамики, клеточных автоматов, в которых рассмотренные соотношения играют главную роль.