1.7 Класифікація систем керування за характером перетворення

сигналів у часі.

За характером перетворення сигналів, які діють у системі, системи керування поділяються на неперервні та дискретні.

Неперервні системи керування характеризуються тим, що значення сигналів у всіх точках, а також змінні стану, є неперервними функціями часу . Приклад неперервної системи керування (Рис.31)

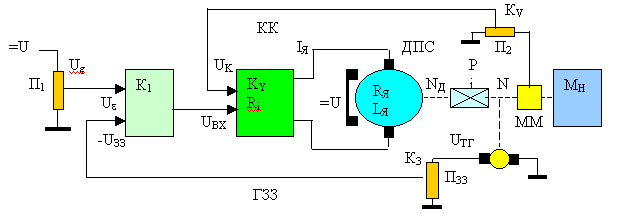
Рис. 31 Типова неперервна система керування швидкістю обертання валу навантаження ДПС

1.7.1 Дискретні системи автоматичного керування.

Дискретними називаються системи, в яких перетворення сигналів у деяких точках здійснюються тільки у дискретні моменти часу , де – період дискретності.

Дискретна послідовність виникає в результаті квантування неперервних сигналів у дискретні моменти часу, яке здійснюється у квантувателях (імпульсних елементах, пристроях вибірки-зберігання), реалізованих за тим чи іншим принципом квантування.

Цифрове керування являє собою більш сучасну форму керування, ніж звичайна. Функції керування за допомогою ЦОМ значно складніші та різноманітніші

При безпосередньому керуванні (Рис.32) автоматичні регулюючі пристрої використовуються в одному контурі з ЕОМ, яка розподіляє їх роботу роздільно у часі. Програмне керування - це вироблення системою керування процесів певної послідовності процедур та керуючих дій, при якому керування здійснюється за допомогою автоматичних регуляторів шляхом подачі сигналів сталих значень на контрольовані точки або забезпечувати ввід керуючих впливів за допомогою подачі команд для пуску та зупинки окремих процесів.

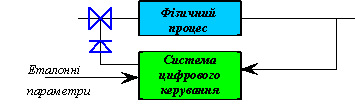
Рис.32 Система безпосереднього цифрового керування

Таким чином, дискретними називаються системи автоматичного керування, у контурах керування яких здійснюються дискретні перетворення сигналів у вигляді послідовності імпульсів або цифрових кодів.

У технічній літературі по керуванню часто-густо зустрічаються терміни "імпульсні системи”,” дискретні системи”,” цифрові системи”, які трактуються досить довільно. Тому у подальшому слід визначити ,який термін треба використовувати до тієї чи іншої системи. Отже, термін "імпульсні системи" слід використовувати у тих випадках, коли у системі є квантуючи пристрої з амплітудною, фазовою або широтно-імпульсною модуляцією, при яких інформаційним показником виступають деякі фізичні властивості імпульсів.

Термін "цифрові системи використовується до систем, у яких сигнали генеруються цифровими пристроями у вигляді цифрових кодів з подальшим їх перетворенням у неперервний вплив для зміни стану змінних процесу.

Термін "дискретні системи” застосовується для опису всіх систем, в яких спостерігається перетворення сигналів у дискретні моменти часу незалежно від прийнятого у системі закону модулювання сигналів. Тому він характеризує системи у більш загальному використанню.

Розглянемо типову імпульсну систему керування із зворотним зв’язком, яка має квантуючий пристрій у прямому ланцюгу передачі сигналу (Рис.33)

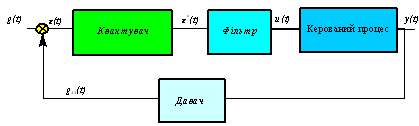
Рис. 33 Імпульснa системa керування

Неперервний сигнал похибки квантується у часі, при цьому вихідний сигнал квантування (квантуючого пристрою) представляє собою послідовність імпульсів з деякими фізичними властивостями. Фільтр, який розміщений між квантувателем та керованим процесом, забезпечує згладжування, тому що більшість фізичних процесів використовують неперервний (аналоговий) сигнал.

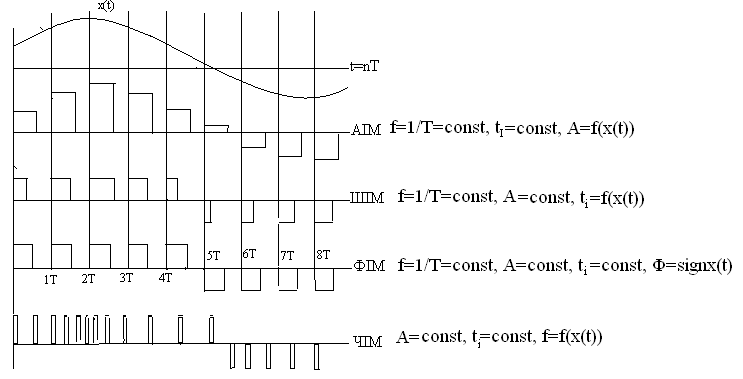
Рис. 34 Принципи імпульсного квантування

У залежності від засобу квантування розділяють квантуючі пристрої з амплітудно-імпульсною модуляцією з широтно-імпульсною модуляцією та фазо-імпульсною модуляцією для яких період T₀ послідовності імпульсів є сталим, а інформаційними показниками сигналу виступають, відповідно, амплітуда, тривалість, фаза імпульсів, та з частотно-імпульсною модуляцією при якому інформаційним параметром сигналу є частота f виникнення імпульсів (Рис. 34).

Типова імпульсна система керування з амплітудною імпульсною модуляцією представлена на Рис.35

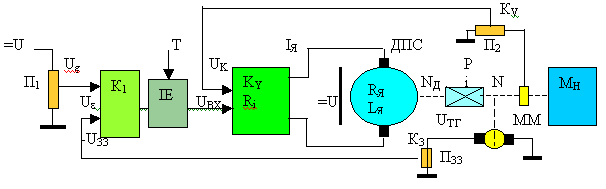
Рис. 35 Типова імпульсна система керування швидкістю обертання валу

навантаження з ДПС

У цифрових системах керування (Рис.36) сигнали у деяких точках системи перетворюються у цифровий код, яким подалі оперує цифрова машина. При цьому квантування сигналу здійснюється аналого-цифровим перетворювачем АЦП та цифро-аналоговим перетворювачем ЦАП. При цьому, якщо ЦОМ виконує тільки пропорційне перетворювання сигналу, то пристрої АЦП-ЦОМ-ЦАП можна визначити як деякий квантуючий пристрій, який виконує модуляцію сигналу за амплітудою та рівнем, при сталій частоті послідовності імпульсів. Процес перетворення сигналу у АЦП можна представити як модуляцію послідовності -імпульсів неперервним сигналом з подальшим перетворенням у цифрову форму , яка залежить від числа N діючих розрядів перетворювання (Рис.37)

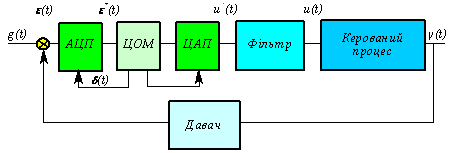
Рис. 36 Цифрова система керування

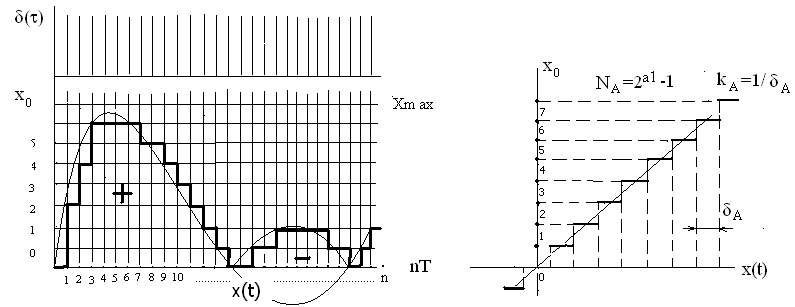
Рис. 37 До принципу квантування по рівню та часу

На виході ЦОМ після обробки сигналу теж з'являється кодований сигнал, який перетворюється у ЦАП у аналогову форму , значення якого змінюється тільки у дискретні моменти та є стійким між цими моментами (Рис. 38 )

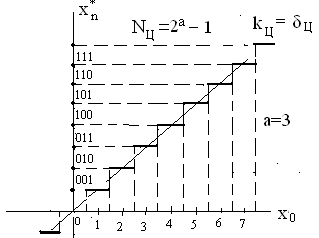
Рис.38 Статична характеристика ЦАП

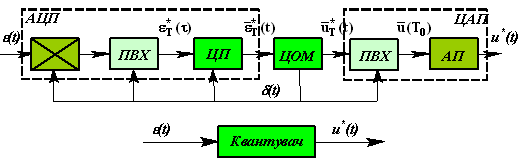
Рис.38 Основний цифровий канал керування

Отже, простішу дискретну систему можна зобразити як сполуку ідеального квантуючого пристрою, формуючої ланки та неперервної частини ( Рис.40).

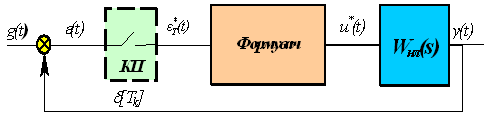
Рис. 40 Ідеальний квантуючий пристрій в системі керування

Ідеальний квантуючий пристрій (імпульсний елемент ІЕ) здійснює модуляцію дельта-послідовності неперервним сигналом

(16)

Отже, на виході ІЕ з'являється послідовність дельта-імпульсів, які нормовані значенням неперервної величини, яке вона має у момент дії імпульсу. Ця послідовність поступає на вхід формувальника, який у залежності від прийнятого принципу дії формує фізичний імпульсний сигнал , який діє на неперервну частину системи . Таким чином, роботу дискретної системи можна розглядати таким чином: замикання системи виконується тільки для дискретного моменту , в моменти ,тобто між дією імпульсів, система працює як розімкнена.

Треба визначити, що у випадках, коли частота переривання сигналу значно більше максимальної частоти амплітудно-частотних характеристик неперервної частини системи, то дискретні системи можна розглядати як неперервні та виконувати її дослідження методами теорії неперервних систем.

Тому що замикання дискретної системи виконується тільки у дискретні моменти часу, тобто у моменти знімання даних аналогового сигналу, тому і методи опису дискретних систем основуються на дослідженні сигналів тільки у дискретні моменти, які визначають замкнений стан системи.

Отже, у моменти дії на неперервну частину системи імпульсів визначної фізичної форми , динаміка системи описується рівнянням

, (17)

а у періоди між ними – однорідним диференційним рівнянням , ₍₁₈₎

Отже, якщо початкові умови визначені, то на основі методу припасовування рішень та можна визначити загальне рівняння, яке описує динамічні процеси у дискретних системах

Приклади дискретних систем керування .

1.Автопілот [ 5]. На рис.41 показано спрощену структурну схему аналогового автопілота для одного керованого параметру(кут тангажу, рискання або крену) літального апарату. Це типова неперервна система, у якої всі сигнали представлені як функції від неперервного часу . Ціллю керування є слідкування пристрою регулювання кута орієнтації апарату за командним сигналом.

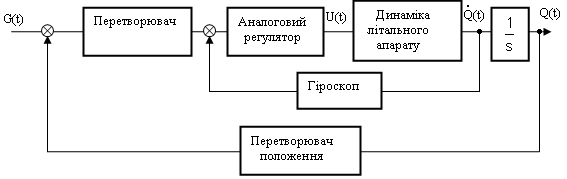
Рис.41 Спрощена схема аналогового автопілоту

Для підвищення стійкості системи введено зворотний зв'язок за швидкістю. Аналоговий регулятор в системі може бути замінено цифровим, при цьому додатково застосовуються аналоговоцифровий та цифро-аналоговий перетворювачі (рис.42). Замість самого регулятора використовується мікроконтроллер, решта елементів системи остаються аналоговими. Така система є системою з однократним квантуванням.

На рис.43 приведено схему цифрового автопілоту, в якому сигнали, що несуть інформацію про положення та швидкість літального апарату, поступають від цифрових пристроїв . Якщо швидкість зміни у одному з контурів буде значно меншою ніж у другому, то і час квантування сигналів може бути різним. Така система стає системою з багатократним квантуванням.

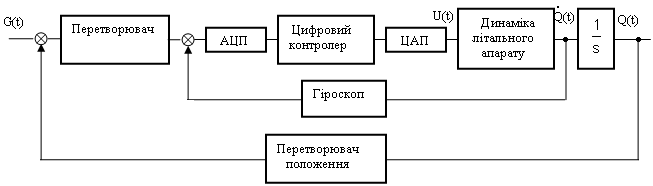
Рис. 44 Спрощена схема цифрового автопілоту

Рис. 45 Спрощена схема цифрового автопілоту з багатократним квантуванням/

2.Цифрова система керування турбіною та генератором. На рис.40 показано структурну схему та основні елементи міні процесорної системи керування швидкістю та напругою блоку турбіна – генератор з підсистемою одержування цифрових даних. Цифроаналогові перетворювачі утворюють інтерфейс між МК та регуляторами. Підсистема отримання цифрових даних вимірювання та увід у МК таких параметрів як кутова швидкість генератора, вихідну напругу, струм збудження та струм якорю, активну та реактивну потужність.

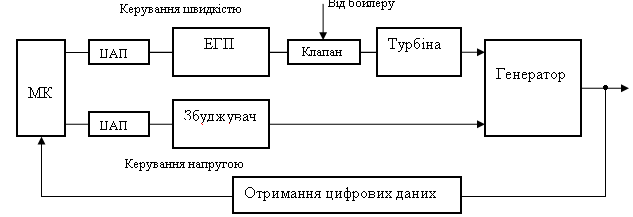
Рис. 46 Цифрове керування блоком турбіна- генератор.

1. ЕГП – електрогідравлічний перетворювач

Деякі з цих параметрів вводяться у МК через цифровий мультиплексор (рис.47).

Рис. 47 Підсистема отримання цифрових даних

Фіксатор зберігає значення сигналу на виході до закінчення перетворення цього сигналу аналого–цифровим перетворювачем у цифровий код ( рис. 48 ).

Пристрій, який включено після мультиплексора, використовуються у режимі розподілу часу. Вихід аналогового мультиплексору сполучається з входом квантуючого пристрою.

Рис. 48 Підсистема отримання цифрових даних з аналоговим перетворювачем

3. Система керування шаговим двигуном. На рис 49 показано систему, яку застосовано для керування головкою зчитування запису дисководу .Для переміщення головки використовується шаговий двигун, який керується командними імпульсами. Ротор шагового двигуна переміщується на строго визначений крок у відповідь на кожний вхідний імпульс. Таким чином, система може бути класифікована як повністю цифровою.

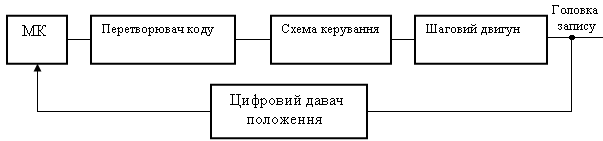
Рис. 49 Система керування шаговим двигуном