1.3 Класифікація систем автоматичного керування за ціллю керування.

В залежності від цілі керування, тобто від потрібного характеру змінювання керованої величини системи керування прийнято поділяти на :

• системи стабілізації, тобто системи, які підтримують регульований параметр на необхідному значенні ;

- системи програмованого керування, які забезпечують необхідну зміну керованої величини згідно з наперед заданим законом зміни збуджуючого впливу ;

- слідкуючі системи керування, які забезпечують зміну керованої величини згідно з наперед відомою функцією часу, яка визначає заданий вплив ;

- кібернетичні системи, які забезпечують підтримку оптимальних значень цільових функцій при неповній інформації про керований процес та діючих на нього збуджувань

1.4 Класифікація систем автоматичного керування за математичним описом оператора системи.

За математичним описом оператора всі системи поділяються на два класи : лінійні системи та нелінійні.

1.4.1 Лінійні системи автоматичного керування.

Дослідження систем автоматичного управління, яке необхідне для наукового обґрунтування їх проектування, засновано на математичних моделях, які відображають властивості реальних систем та служать безпосереднім об'єктом дослідження.

При описі систем управління у першому наближенні модель, як правило, є лінійною. При цьому дослідження таких систем є відносно простим, а результати достатньо прозорими. В теорії дослідження лінійних систем, окрім підходу, який засновано на застосуванні диференційних рівнянь та розглядання явищ у часовій області, використання змінних стану, ефективними є й методи, основані на перетвореннях Фур'є та Лапласа, які оперують із зображеннями у площині комплексного змінного та у частотній області.

Дякуючи теоремам Ляпунова про стійкість по першому наближенню теорія лінійних систем служить основним інструментом при дослідженні стійкості реальних систем при малих збудженнях. При цьому лінійні системи, як правило, мають асимптотичну стійкість, для них також справедливий принцип суперпозиції.

У лінійних системах із сталими параметрами поведінка вихідної змінної не залежить від величини вихідної змінної, а визначається тільки оператором перетворення системи А, який є її повною характеристикою.

.

Оператор А називається лінійним, якщо при будь-яких числах та будь-яких функціях виконуються рівняння

(10)

Властивість, яка виражена цією формулою зветься принципом суперпозиції і складається з того, що результат дії лінійного оператора на будь-яку лінійну комбінацію заданих функцій є лінійною комбінацією від результату його дії на кожну функцію з такими ж коефіцієнтами

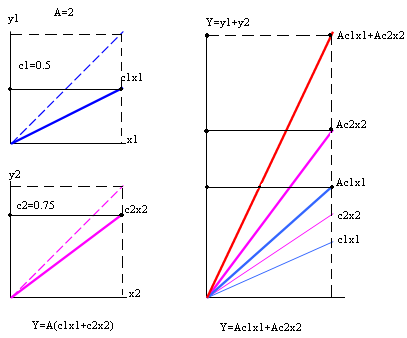
Рис.25. До пояснення принципу суперпозіції

Автоматична система лінійна, якщо лінійний її оператор (тобто для неї справедливий принцип суперпозиції), який дозволяє досліджувати поведінку системи як результат дії кожного впливу (як задаючого, так і збуджуючого) незалежно один від одного. Так для системи поданої на Рис.25 справедливо твердження, що вихідна величина складається із часток дії задаючого впливу та збуджуючого впливу , тобто

Лінійну систему можна ще визначити як систему, динаміка елементів якої описується лінійними рівняннями: алгебраїчними, диференційними або дискретними. При цьому статичні характеристики всіх елементів системи повинні бути лінійними.

Для наведеної схеми системи повинна виконуватись лінійність кожного оператору , , , тобто , де ; .

Якщо динаміка всіх елементів системи описується звичайними лінійними диференційними рівняннями із сталими коефіцієнтами, то систему називають звичайною лінійною системою, або детермінованою стаціонарною системою.