5. Визначається перехідний процес

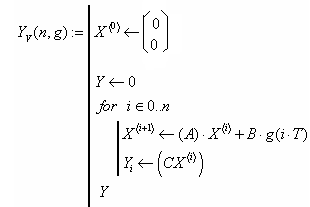
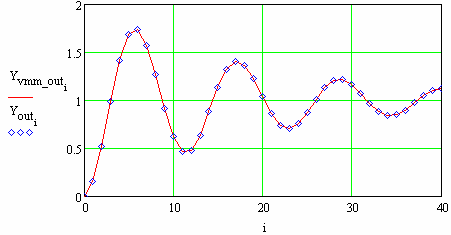
Рис. 153 Перехідний процес пробудований по ВММ

П 29

Для дискретної системи керування, неперервна частина якої має передаточну функцію

1. Визначається передаточна функція умовно розімкнутої системи у Z-формі методом

розкладу на прості дробі

Знаходяться невизначені коефіцієнти та визначається

1.4 Визначається передаточна функція замкнутої системи

1. Виконується розв’язання дискретного рівняння

Початкові умови

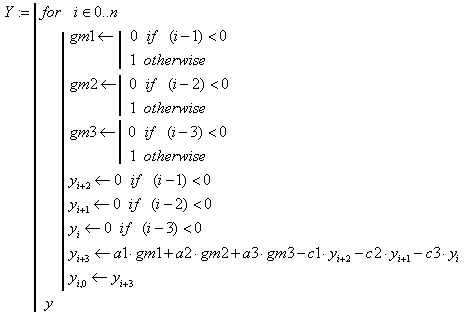
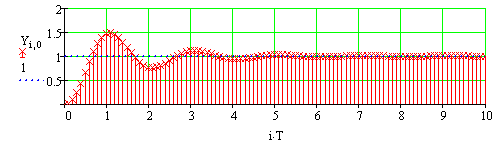
Рис.154 Перехідний процес побудований подискретному рівнянню

2. Складається векторна матрична модель

0. Виконується розв’язання векторно матричного рівняння

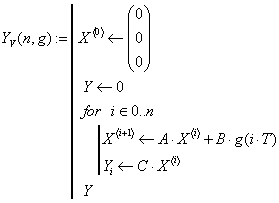
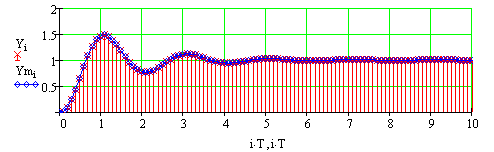
Рис 155 Перехідний процес побудований по ВММ з перевіркою по дискретному рівнянню—процеси співпадають

П 30

Виконати цифрове моделювання диференційного рівняння

Для спрощення

1. Моделювання за допомогою Z-форм . Крок розв’язання

2. Перевірка

3. Визначається ВММ

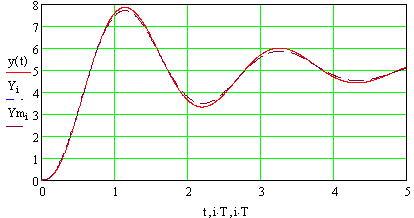
Рис. 156 Перехідні процеси добре співпадають

Лабораторна робота №5 Дослідження методів цифрового моделювання

Призначення: Лабораторні дослідження націлені на закріплення знань основних підходів до цифрового моделювання основних методів цифрового інтегрування та диференціювання, можливості на їх основі складати моделі типових алгоритмів цифрового моделювання

Ціль роботи: Закріплення знань особливостей цифрового інтегрування по методу прямокутників та методу трапеції, методів цифрового диференціювання , особливостей складання типових алгоритмів для реалізації їх на основі мікроконтролерної техніки.

Вибір структури та її параметрів блоків інтегрування та диференціювання виконується виходячи із аналізу функціональної схеми блока моделі узагальненої системи керування віртуального лабораторного стенда та обраних цілей лабораторних досліджень. Значення параметрів системи обирається із таблиці варіантів

В лабораторній роботі необхідно:

1. Скласти математичну модель процесу інтегрування по методу прямокутників

2. Скласти математичну модель процесу інтегрування по методу трапецій

3. Виконати експериментальні дослідження та порівняти здобуті результати

4. Виконати експериментальні дослідження диференціювання гармонічних сигналів

5. Визначити вплив періоду квантування на точність реалізації типових алгоритмів

Висновок. Відповідно теоретичним розрахункам та обробки експериментальних досліджень зробити висновки по лабораторній роботі згідно обраних цілей.

215