1.2.2 Принцип замкнутого керування.

Чи можна використати інформацію про відхилення величини керування від потрібного значення , незалежно від причин, які спричинили таке відхилення, та побудувати систему керування, яка підтримувала б вихідну величину на потрібному значенні?

Поміркуємо! Нехай значення вихідної величини визначається відношенням

де – ідеальний оператор перетворення системи.

У результатi дiї збудження дiйсне значення буде вiдрiзнятися вiд на величину

Але така постановка задачi потребує органiзацiї системи збору iнформацiї про характер змiни керованої величини, тобто необхiдний контроль результату дiї зовнiшнiх впливiв та порiвняння його з потрiбним значенням та виробки додаткового управляючого впливу .

Нехай у найпростому випадку , тобто .

Тоді , тобто вiдхилення дорiвнює результату порiвняння завдання та виходу , для чого у системi створюється канал від’ємного зворотного зв'язку. При цьому вiдбувається замикання системи, при якому iнформацiя про результат дiї подається до входу системи на датчик розузгодження (Рис.21). Оператор зворотного зв'язку служить для перетворення вихiдної величини до вигляду, здатного для порiвняння із задаючим впливом .

Таким чином, система рівнянь та співвідношень у такій системі приймає наступний вигляд :

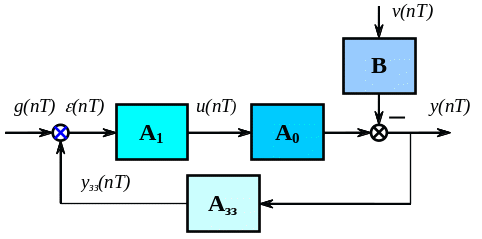
Рис. 21 Схема системи із замкнутим принципом керування

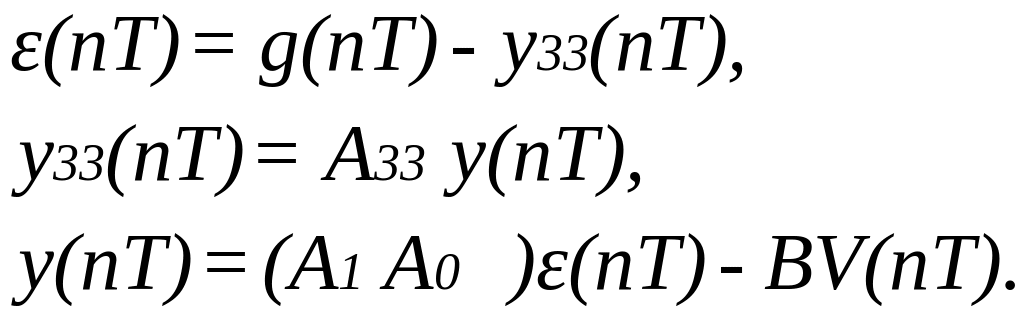
Розв'язавши систему рівнянь відносно задаючих та збуджуючих впливів отримуємо

. (6)

Для порівняння результату дії замкненої системи з розімкнутою покладемо

Тоді , де коефіцієнт визначає статизм характеристики навантаження, який показує у кілька разів замкнутий принцип керування точніше розімкнутого (Рис.22). Очевидно, що при дія збуджуючого впливу зводиться до нуля

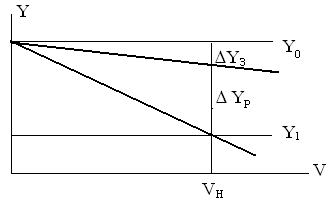
Рис.22 Порівняльні характеристики навантаження в системах розімкнутого та замкнутого принципів керування

При цьому закон керування буде визначатися як , а типова система керування з ДПС приймає вигляд (Рис.23)

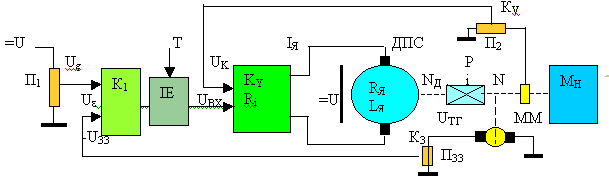
Рис. 23 Типова система керування ДПС із законом керування по відхиленню

Таким чином у замкненій системі реалізується Закон керування за похибкою регульованої величини від заданого впливу, тобто замкнений закон керування.

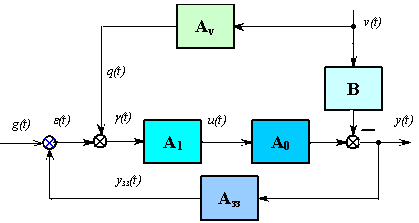
Рис.24 Схема замкнутого керування з комбінованим законом керування

Якщо неможливо побудувати систему керування із пристроєм, який має нескінченно великий коефіцієнт підсилення, але є можливість контролювати збудження, то можливо реалізувати комбінований закон керування за відхиленням та збуджуючим впливом

₍₇₎

Функціональні співвідношення окремих елементів приймають вигляд

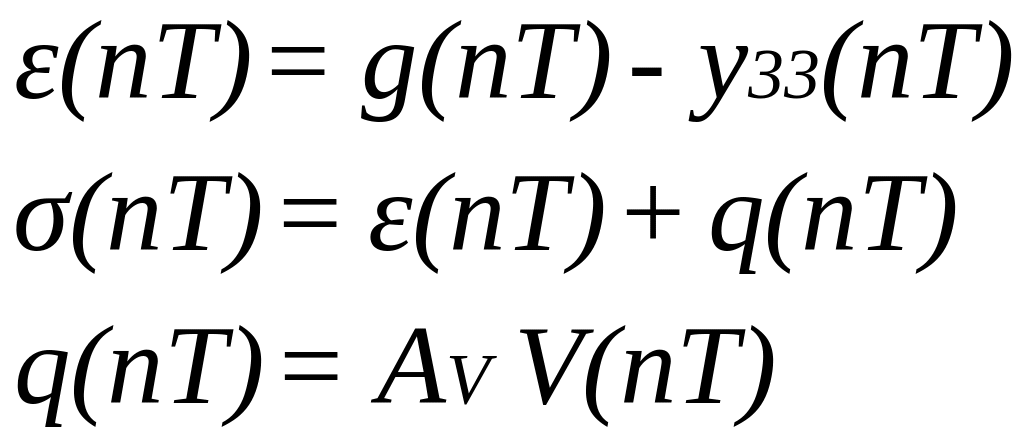
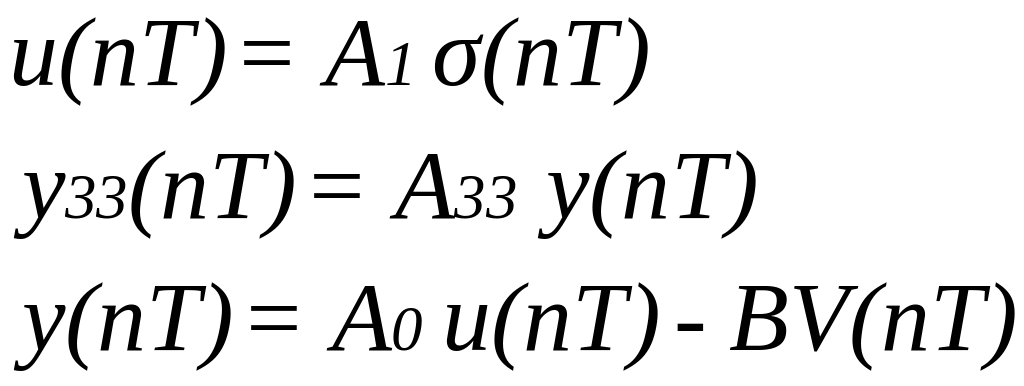
які дають змогу здобути основне рівняння виходу

(8), яке показує, що для повної компенсації впливу збудження потрібно додати канал компенсації з перетворюючими властивостями, які визначаються співвідношенням

(9) При цьому замкнена система керування набуває позитивних властивостей розімкненої.

Зверніть увагу! Сумарний вплив каналів передачі збуджуючого впливу повинен дорівнювати нулю , тобто канал компенсації завжди діє з протилежним знаком порівняно із знаком дії каналу передачі збуджування у об'єкті керування.

  Висновки :

1. Системи, побудовані за розімкненим принципом керування, мають підвищену швидкість відпрацювання збуджуючого впливу.

2. Системи з принципом керування по відхиленню мають більшу точність відпрацювання збуджуючих впливів без контролю самих діючих на систему збуджень.

3. В системах комбінованого керування за рахунок вибору оптимального значення оператора каналу компенсації можливо зробити систему інваріантною по відношенню до збуджуючого впливу.