2.11.6 Цифрове моделювання неперервних систем керування.

Методи дискретного опису систем автоматичного керування можуть з успiхом застосовуватися для моделювання процесiв у аналогових системах.

Подібний процес звичайно складається з наступних етапiв:

1) Опис неперервної системи за допомогою дискретних моделей.

2) Особисте моделювання на ЦОМ.

При виконаннi цифрового моделювання, як правило, використовуються три методи:

1) введену у неперервну систему пристроїв вибiрки та зберігання;

2) чисельне iнтегрування;

3) апроксимацію за допомогою -форми.

Розглянемо неперервну систему (Рис.145), з наступним її перетворенням у дискретний варiант шляхом застосування фiксаторiв нульового порядку.

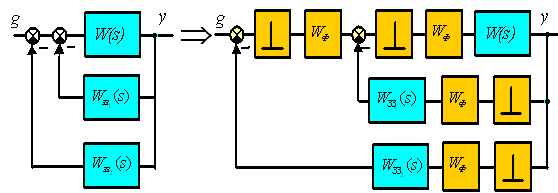
Рис. 145 Цифрове моделювання неперервної системи

При цьому

При переходi до розрахункової математичної моделi у -формi необхiдно вибрати перiод квантування, який суттєво впливає на точнiсть моделювання та на схожiсть процесiв. Тому при виборi перiоду квантування треба виходити з нього, щоб у процесi рiшення не утратити швидкозгасаючі складовi частки перехiдних процесiв, якi обумовленi великими дійсними частками нулiв та полюсiв передаточної функцiї. Тому вибiр перiоду квантування при переходi моделi до дискретної повинен задовольняти умови

, де - коренi характеристичного полiному замкненої системи, що забезпечує достатньо наближеність показникiв якості дискретної та неперервної моделей.

Метод моделювання за допомогою - форми засновано на взаємозв'язку з

-зображенням

Якщо представити у виглядi розкладу у ряд

то

Для зручностi розрахункiв (з достатньою для практики точнiстю) можна обмежитись першим членом ряду.

Тодi

Узяв два члена ряду, здобудемо

Вiдповiдно обчислюються наступнi степенi

Хай

Отже,

а

При цьому

Хай неперервна система описується рiвняннями вигляду

.

Вiдомо, що рiшення можна здобути у формi

.

Зафiксуємо момент часу , та , де – такт дискретностi, який обумовлює вибiрку з процесiв та . Тодi стан системи у моменти часу зв'язано з попереднiм станом у моменти часу спiввiдношенням

тобто залежить вiд змiни вхiдного сигналу на інтервалі дискретностi. Форма сигналу на iнтервалi дискретностi визначається чином пристрою квантування. При фiксаторi нульового порядку

,

що приводить до наступної дискретної моделi

де - перехiдна матриця системи

- матриця коефiцiєнтiв передачі по входам дискретної моделi.

Якщо при застосуваннi квантователя використовується екстраполятор першого порядку, за яким вхiдний сигнал на iнтервалi дискретностi змiнюється по лiнiйному закону, то

При цьому

де

По вiдомим матрицям та можуть бути реалiзованi вiдповiднi методи чисельного iнтегрування Рунге-Кутта

1. Метод першого порядку.

Рис. 146 Реалізація методу першого порядку

2. Метод другого порядку.

Рис. 147 Реалізація методу другого порядку

3. Метод третього порядку.

Рис. 148 Реалізація методу третього порядку

4. Метод четвертого порядку.

Рис. 149 Реалізація методу четвертого порядку

Цi схеми моделювання показують, що моделi методiв Рунге-Кутта мають додатковi погрiшностi, якi обумовленi розкладом матрицi та матрицi у ряд Тейлора (так, 4-й метод використовує тiльки чотири члени розкладу функцiї ), що викликає накопичення похибки у процесi чисельного iнтегрування.

П 27

Визначити перехідний процес за допомогою ВММ якщо

1. Перехідний процес по матрицям ВММ

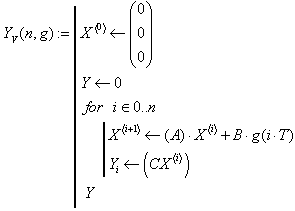
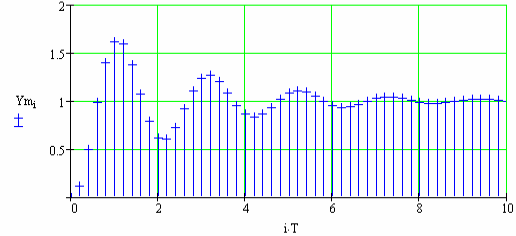
Рис. 150 Перехідний процес побудований по ВММ за першим методом

2. Другий метод побудови перехідного процесу

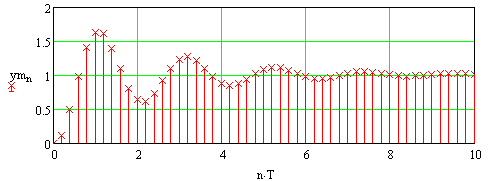
Рис. 151 Перехідний процес побудований по ВММ за другим методом

П 28

Визначити ВММ та побудувати перехідний процес

-одинична функція Хевисайда

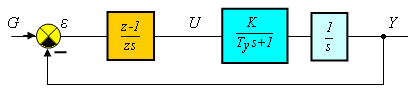
1. Визначається передаточна функція умовно розімкнутої системи с фіксатором нульового порядку

2. Визначається передаточна функція умовно розімкнутої системи с фіксатором нульового порядку у Z-формі

3. Передаточна функція замкнутої системи

3. Визначається зображення вихідного сигналу

Виконується заміна

4. Визначаються матриці ВММ методом нормальних змінних

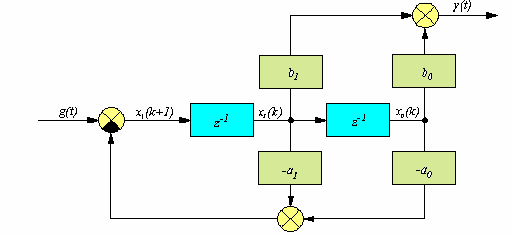
_{Рис.152 Структурна схема системи у змінних стану}