2.9.2 Критерій Михайлова.

Для стiйкості дискретної системи автоматичного управлiння необхiдно i достатньо, щоб годограф Михайлова переходив у даному напрямку квадрантів при змiнi частоти вiд до пiде не перетворюючись у нуль, починаючись та закiнчуючись на дiйснiй пiвосi.

Для стiйкості дискретної системи автоматичного управлiння необхiдно i достатньо, щоб годограф Михайлова переходив у даному напрямку квадрантів при змiнi частоти вiд до пiде не перетворюючись у нуль, починаючись та закiнчуючись на дiйснiй пiвосi.

Критерiї Михайлова може бути сформульовано на основi правила чергування коренiв дiйсної та уявної частин характеристичного полiному :

для стiйкості дискретної САУ необхiдно та достатньо, щоб дiйсна та уявна частини годографу Михайлова мали дiйсних переміжних коренiв (Рис.135).

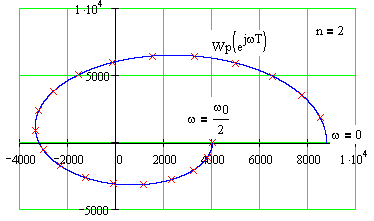
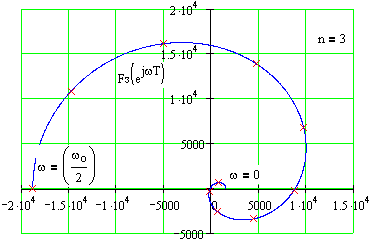
Рис.135 Приклади годографів Михайлова для стійких дискретних систем

П

Побудувати годограф Михайлова, якщо

1. Визначається характеристичний поліном замкнутої системи

2. Виконується перехід до частотної характеристики заміною

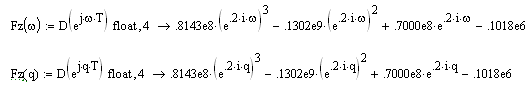
3. Визначається частотний діапазон побудови годографа Михайлова

4. Будується годограф Михайлова

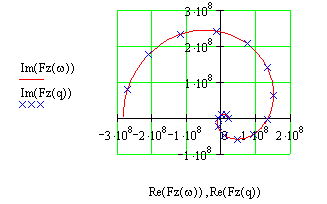
Годограф проходить 2n квадрантів у додатньому напрямку (проти ходу годинникової стрілки) охоплюючи початок координат. Система стійка.

5. Слідство

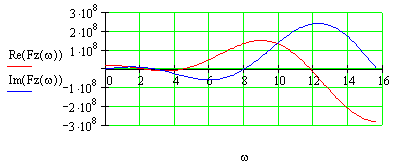
Корені дійсної та мінливої частин переміжуються. Система стійка.

2.9.3 Критерій Найквіста.

Розглянемо умови стійкості дискретної системи. Характеристичний вектор замкнутої системи представимо у вигляді

Якщо розiмкнена система стiйка, тобто |, та стiйка замкнена система , то згiдно принципу аргументу

(143)

для того, щоб замкнена цифрова дискретна система, яка має у розiмкненому станi полюсiв , була стiйкою, необхiдно i достатньо, щоб годограф не охоплював точку при змiнi частоти у дiапазонi вiд

до (Рис.136).

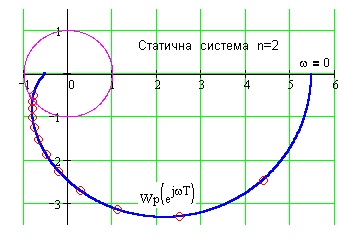
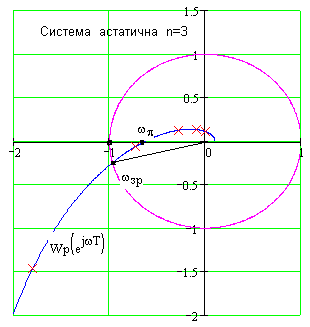
Рис.136 статичної системи Рис.137 астатичної системи

Якщо ж розiмкнена система нестiйка i має правих коренiв , а замкнена система стійка , то

(144)

Отже, характеристичний вектор починається та закiнчується на додатнiй осi та перемiщується проти часової стрiлки, тобто у додатному напрямку. Якщо перенести початок координат у точку , то здобудемо аналог критерiю Найквiста для дискретних систем.

Для того, щоб замкнута дискретна система, яка у розiмкненому станi має полюсiв у комплексної площинi була стiйкою, необхiдно i достатньо, щоб годограф охоплював у додатному напрямку точку разiв при змiнi частоти у дiапазонi вiд разiв при змiнi частоти у дiапазонi вiд

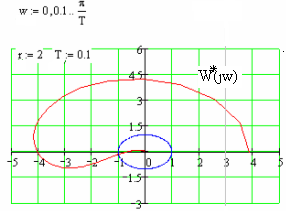
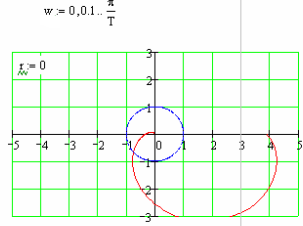
Рис.138 Годограф Найквіста для стійких систем

Якщо розiмкнена система стiйка, то для того, щоб стiйкою була замкнена система необхiдно i достатньо, щоб годограф не охоплював точку (Рис.138).

П

Побудувати годограф Найквіста

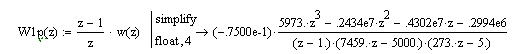
1. Виконується перехід до частотної характеристики заміною . Визначаються дійсна та мінлива частини та виконується прив’язка до частоти

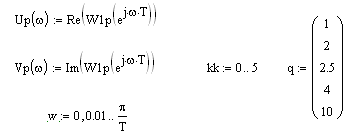
2. Будується годограф Найквіста

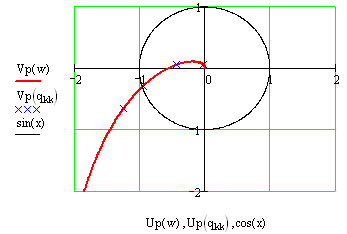
Годограф Найквіста не охоплює точку (-1,j0). Система стійка

П 2.50

Визначити стійкість дискретної системи, яка у розімкнутому стані має у неперервної частини два правих кореня

1. Визначається передаточна функція умовно розімкнутої системи у Z-формі

2. Визначається передаточна функція замкнутої системи та розраховується перехідний процес

3. Визначається АФЧХ умовно розімкнутої системи підстановкою

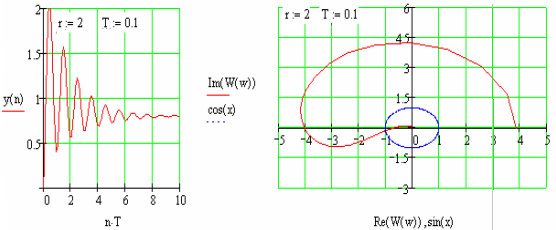
Рис.139 Перехідний процес та частотна характеристика до П

Перехідний процес збігається, годограф Найквіста охоплює критичну точку y додатньому напрямку один раз. Отже, замкнута система стійка.