2.7.1 Дослiдження швидкодiї та коливальностi дискретних систем управлiння

Швидкодiя та коливальність дискретних САУ залежить вiд швидкостi згасання та коливальностi вiльних складових yві перехiдних послідовностей, якi в свою чергу залежать вiд характеристик вагової послідовності.

Представимо) таким чином

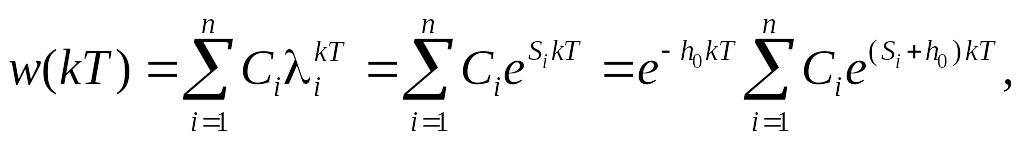
де та S_i коренi характеристичного рiвняння дискретної системи у площинах змiнних Z та S вiдповiдно, а h₀>0 є деякою дiйсною сталою, яка визначається як

(126)

тобто є степенем стiйкостi.

Очевидно, що степiнь стiйкостi h₀ може бути знайдено за умови находження системи на межi стiйкостi по зміщеної iмпульсної передаточної функцiї W*(jw,h₀), тобто

Але у площинi Z пряма h₀ площини S буде вiдображатися як коло радiусу h₀^*, де h₀*=1-h*, тобто у якостi мiри швидкодiї може використатися вiдстань h₀* вiд найближчого полюсу z_i до кола радiусу R=1. Якщо всi коренi z_i нульовi, то перехiдний процес буде скiнчуватися за кiнцеве число тактiв.

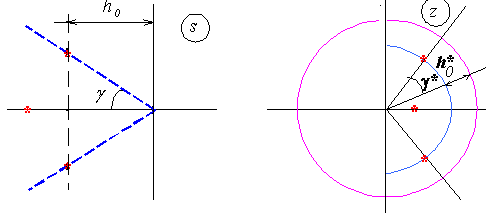
Рис. 108 Степінь стійкості у S та Z площинах

Дiйсно, у випадку, якщо W(z) має вигляд

(127)

розклад у ряд Лорана по степеням

що дає вагову послiдовнiсть, яка має кiнцеве значення вагових коефiцiєнтiв

а це позначає, що вiльна складова перехiдного процесу закiнчується за n тактiв.

Степiнь стiйкостi для подiбних систем дорiвнює нескiнченностi, тому що

тобто нульовому коренi у Z площинi вiдповiдає нескiнченно вiддалений корінь у S площинi.

Коливальнiсть дискретних САУ, як свiдчить вираз

залежить вiд того, чи є корінь , який віддалено вiд дiйсної пiвосi площини Z.

Як i для неперервних систем, оцiнка степенi коливальностi може бути визначена по вiдношенню

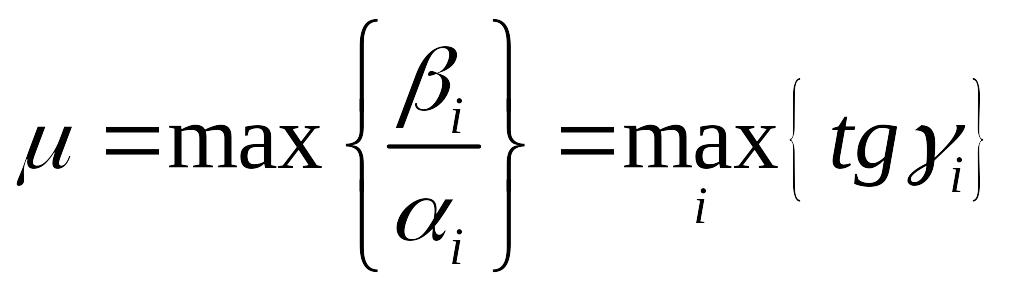(128)

Очевидно, що максимальне перерегулювання у системi залежить вiд та при однiй парi комплексних коренiв має вигляд

де С залежить вiд початкових умов.

П 2.34

Дослідити умови стійкості та вплив структури системи керування на стійкість

Дискретна система 1-го порядку

Передаточна функція неперервної частини . Імпульсний елемент - ФНП

Період квантування , , . Вхідний вплив ,

_{Передаточна функція неперервної частини}

Порядок розрахунку

Визначення передаточної функції розімкнутої системи у формі

1. Передаточна функція ФНП

Визначається часова характеристика

2.

3.

4.

Визначається передаточна функція замкнутої системи

5.

Визначається характеристичне рівняння та його корені

6.

7.

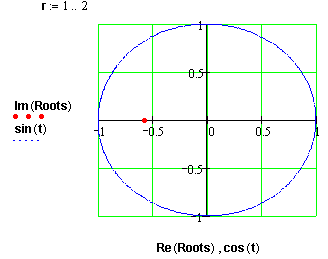
8. Будується перехідний процес

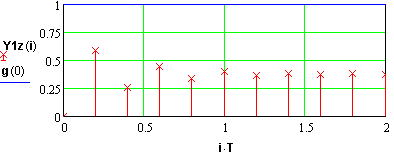
9. Перевіряється стійкість по критерію Михайлова

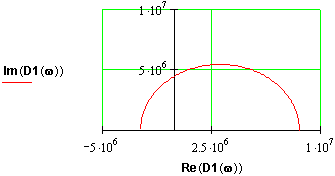
Система стійка

П 2.35

Дискретна система 2-го порядку (астатична)

Розрахунок виконується за попередньою схемою

Передаточна функція неперервної частини

,

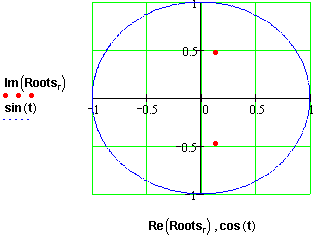
Рис.109 Розташування коренів для системи 2-го порядку

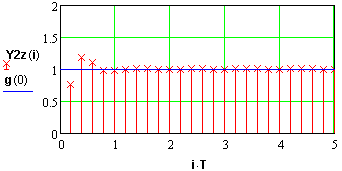
Рис 110 Перехідна характеристика замкнутої системи. Система стійка

П 2.36

Дискретна система 3-го порядку (Астатизм 2-го порядку)

Передаточна функція неперервної частини

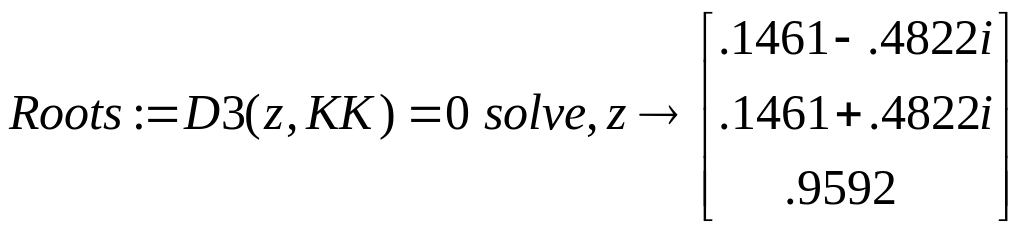
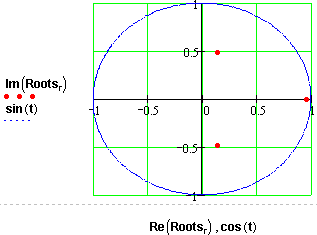
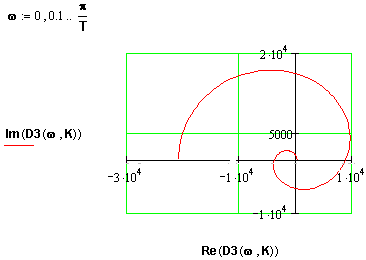
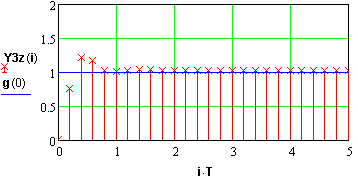
Рис.111 Розташування коренів, частотна характеристика та перехідний процес у стійкий системі 3-го проядку

Траєкторія коренів

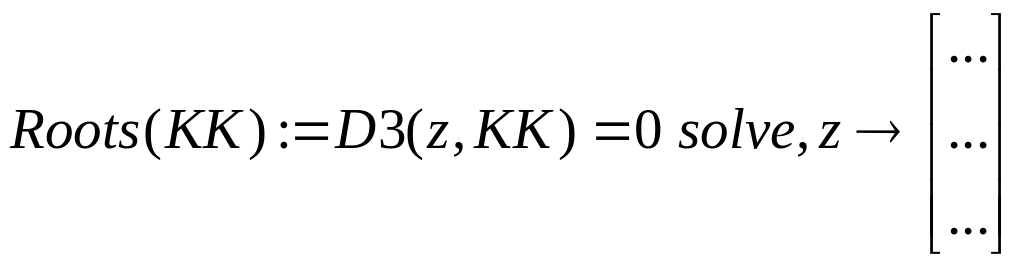
. Положення коренів

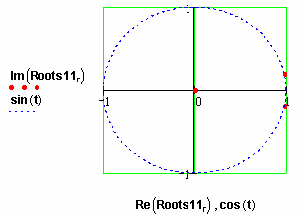
Траєкторія коренів

Початкове значення , Кінцеве значення , Кількість кроків

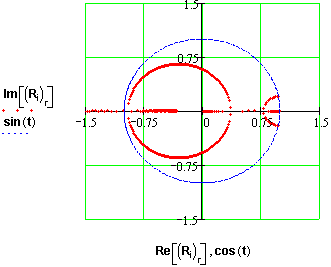
Рис 112 Корневий годограф для системи 3-го орядку

2.6.2 Співвідношення між S- та Z- площинами

Відомо, що Z-перетворення на відображенні на z-площині змінної . Якщо розглядати основну смугу у межах , то контур 1-2-3-4-5-6 на s-площині (Рис.113) відображається у одиничне коло z-площини з центром у початку координат. При цьому можна зробити такі виснавки.

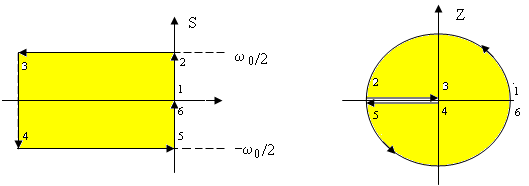
Рис.113 Відображення основної полоси у одиничне коло

Лінія постійного згасання : на S-площині це пряма лінія на відстані від мінливої осі; на Z-площині це коло радіусу (Рис.114).

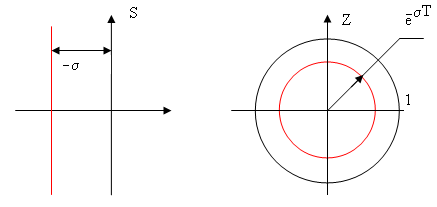
Рис 114 Лінія постійного згасання

Лінія постійної частоти : на S-площині це пряма лінія на відстані від дійсної осі; на Z-площині це лінія, яка виходить з початку координат під кутом (Рис.115)

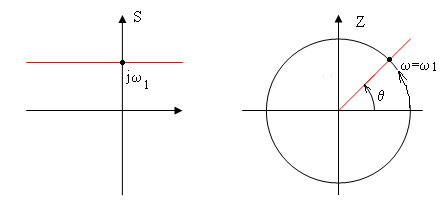
Рис. 115 Лінія постійної частоти

Лінія постійного коефіцієнту згасання : на S-площині це пряма лінія , яка виходить з початку координат під кутом від мінливої осі у додатному напрямку; на Z-площині це логарифмічна спіраль, яка описується рівнянням (129) (Рис.116)

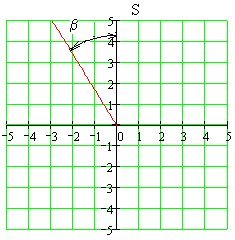
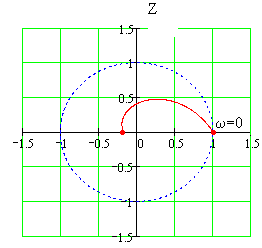
Рис.116 Лінія постійного коефіцієнта згасання

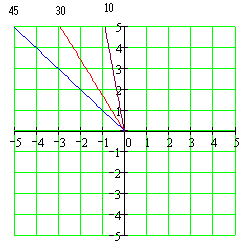
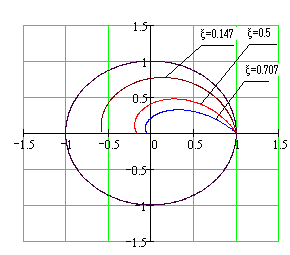
Рис.117 Вплив коефіцієнта згасання

.

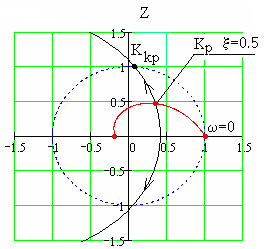Рис. 118 Визначення заданого коефіцієнта підсилювання

Якщо нанести на ці графіки рух коренів при зміні якогось параметру системи (наприклад коефіцієнта передачі),то по точці перетину з лінією згасання можна визначити відповідний коефіцієнт , який буде забезпечувати необхідне згасання.

П 2.37

Для дискретної системи з фіксатором нульового порядку побудувати рух коренів та лінію постійного коефіцієнта згасання .

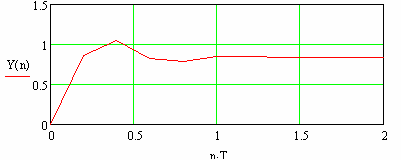
Рис.119 Перехідний процес

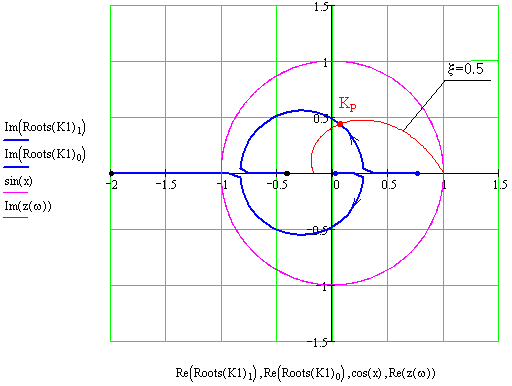
Рис 120 Корневий годограф та визначення заданого коефіцієнта передачі