
- •1.1 Класифікація цифрових систем автоматичного керування по методу використання цифрової обчислювальної машини цом ( мікропроцесорів мп, мікроконтролерів мк ) для цілії керування.
- •1.2 Класифікація систем керування за принципом організації
- •1.2.1 Принцип розімкненого керування.
- •1.2.2 Принцип замкнутого керування.
- •1.3 Класифікація систем автоматичного керування за ціллю керування.
- •1.4 Класифікація систем автоматичного керування за математичним описом оператора системи.
- •1.4.1 Лінійні системи автоматичного керування.
- •1.4.2 Нелінійні системи автоматичного керування.
- •1.5 Класифікація систем автоматичного керування за характером похибки у сталому режиму.
- •1.6 Класифікація за характером зміни оператора системи у часі.
- •1.7 Класифікація систем керування за характером перетворення
- •1.7.1 Дискретні системи автоматичного керування.
- •1.7.2 Функції цифрового керування
- •1.7.3 Безпосереднє цифрове керування
- •1.8 Перетворення та обробка сигналів
- •1.8.1 Цифрові сигнали та кодування
- •1.8.3 Похибки, які визиваються квантуванням за рівнем
- •1.9 Коректування впливу похибки перетворення аналогового сигналу у дискретний.
- •1.10 Перетворення та методи представлення сигналів
- •1.10.1 Перетворення Лапласа
- •1.10.2 Властивості перетворення Лапласа.
- •1.10.3 Перетворення Фур’є .
- •1.10.4 Властивості перетворення Фур’є
- •1.10.5 Дискретне перетворення Лапласа.
- •Для вiдносного часу використовується символьна форма зображення
- •1.10.7 Дискретне перетворення Фур’є
- •1.10.8 Z – перетворення
- •1.10.9 Основнi властивостi -перетворення
- •Вiдповiдно теорiї зсуву
- •Хай дискретне рiвняння має вигляд
- •1.10.10 Процеси мiж моментами квантування (Метод модифікованого - перетворення).
- •1.10.11 W-перетворення
- •1.11 Дискретні сигнали.
- •2.2 Дискретні рівняння систем керування та методи їх розв’язання.
- •2.1.1 Складання дискретних рівнянь лінійних систем
- •2.3 Вагова (імпульсна) перехідна функція дискретної системи.
- •2.5 Передаточні функції дискретних систем керування.
- •2.5.1 Властивостi w(z)
- •2.5.2 Передаточка функція умовно розімкнутої дискретної системи
- •Очевидно, що
- •2.5.3 Передаточнi функцiї замкнених дискретних систем
- •2.6 Умови стійкості дискретних систем керування.
- •Тому що рiшення дискретного рiвняння вiдшукується у виглядi , де вiльна складова, яка є рiшенням однорiдного рівняння
- •2.6.1 Алгебраїчні критерії стійкості дискретних систем. Критерій гурвіця.
- •2.6.2 Критерій Шур-Кона.
- •2.5.3 Критерій Джурі.
- •2.7 Оцінка точностi роботи дискретних систем у сталих режимах
- •2.7.1 Дослiдження швидкодiї та коливальностi дискретних систем управлiння
- •2.8 Частотнi характеристики дискретних систем
- •2.9.2 Критерій Михайлова.
- •2.9.4 Визначення стійкості по логарифмічним характеристикам.
- •Типові ланки та їх характеристики
- •Якщо покласти , , то
- •2.11.1.1 Метод розкладу на елементарнi дробi.
- •2.11.1.2 Метод нормальних змiнних стану. Нехай система описується дискретним рiвнянням
- •2.11.2 Складання вмм дискретної системи
- •Тому що то суттєву роль у визначенні змiнних стану грає вираз який називають матрицею переходу або матричною експонентою.
- •Тодi рiшення рiвнянь стану записується у виглядi
- •Так, якщо задано цифрову систему керування , а матриця визначена як
- •Тому що
- •2.11.4 Визначення передаточної функції дискретної системи
- •2.11.5 Визначення умов стійкості
- •Тому що рiшення цього рiвняння добувається у виглядi
- •2.11.6 Цифрове моделювання неперервних систем керування.
- •При цьому
- •Визначається перехідний процес
2.6.2 Критерій Шур-Кона.
При
використаннi цього критерiю коефiцiєнти
характеристичного полiному
![]()
групуються вiдповiдним чином у пiдматрицi А11 та А21.
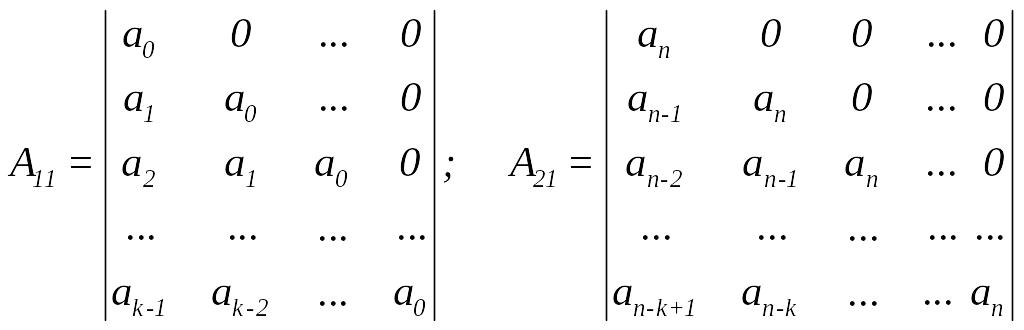
Далi формується блочна матриця порядку 2k
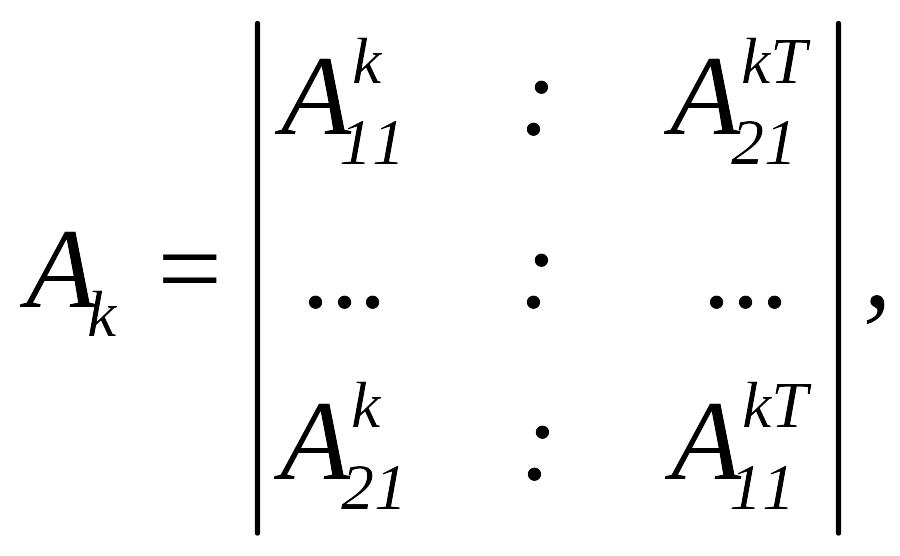
де
![]() -
транспонованi матрицi вiдповiдно до
-
транспонованi матрицi вiдповiдно до
![]() та
та
![]() .
.
Змiнюючи k вiд 1 до n, знаходять знаки визначникiв та перевiряють чергування знакiв
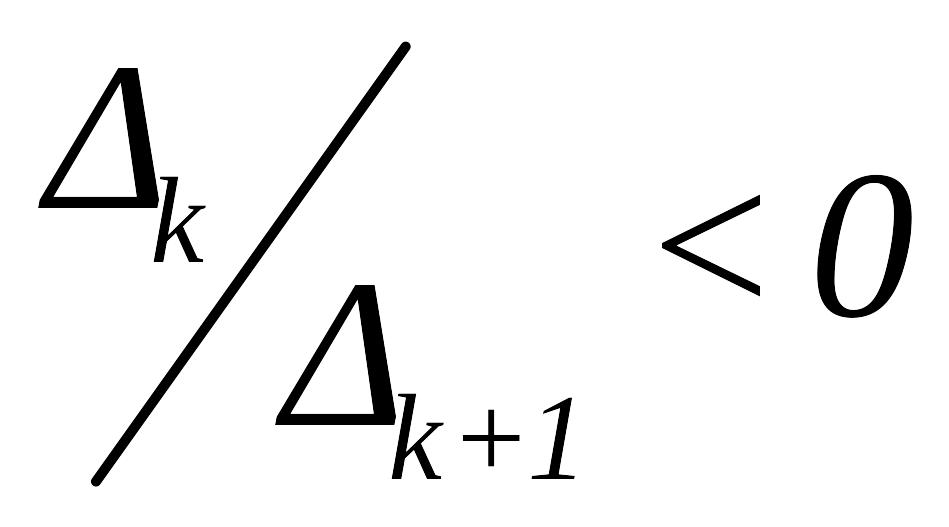 (112)
(112)
Якщо
умови виконуються, то всi коренi полiнома
![]() лежать у серединi кола одиничного
радiусу. Таким чином, якщо всi
лежать у серединi кола одиничного
радiусу. Таким чином, якщо всi
![]() то
немає
то
немає
![]() ,
а число нулiв у серединi кола з
,
а число нулiв у серединi кола з
![]() дорiвнює
числу змiн знакiв у послідовності
дорiвнює
числу змiн знакiв у послідовності
![]()
Хай
![]()
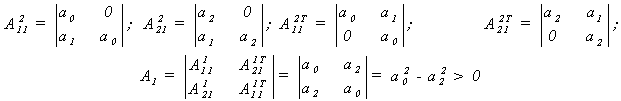
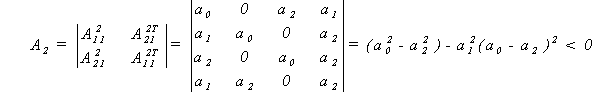
Для системи третього порядку повиннi виконуватися умови
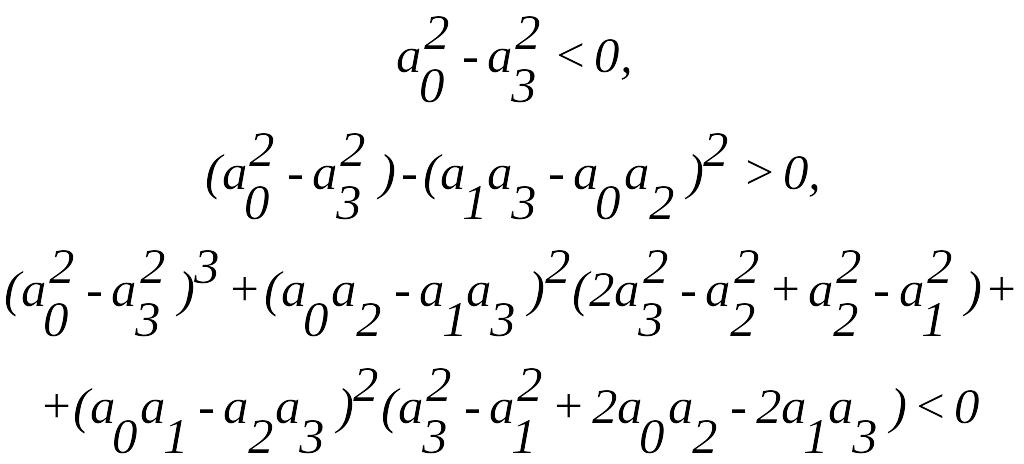
2.5.3 Критерій Джурі.
Запишемо характеристичний полiном у виглядi
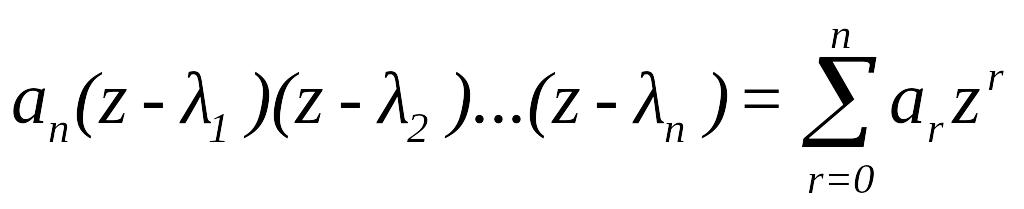 (113)
(113)
та
переставимо у полiномi коефiцiєнти за
правилом
![]() Якщо
записати
характеристичний полiном замкненої
системи керування у виглядi
та
переставити у полiномi коефiцiєнти за
правилом
Якщо
записати
характеристичний полiном замкненої
системи керування у виглядi
та
переставити у полiномi коефiцiєнти за
правилом
![]() ,
то для
,
то для
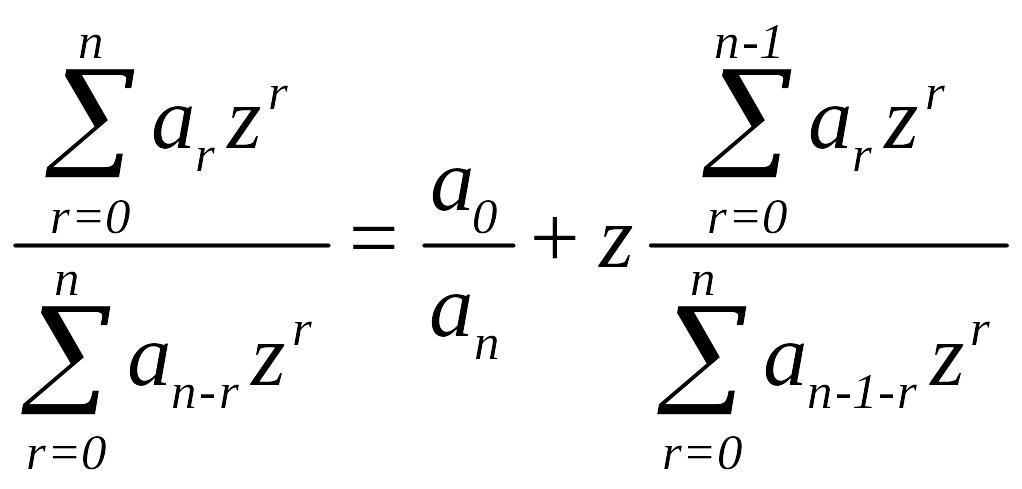 повинна виконуватися
повинна виконуватися
![]() ,
тому що
для початкового рiвняння вiдношення
молодшого коефiцiєнту до старшого
дорiвнює добутку всiх коренiв полiномiв
,
тому що
для початкового рiвняння вiдношення
молодшого коефiцiєнту до старшого
дорiвнює добутку всiх коренiв полiномiв
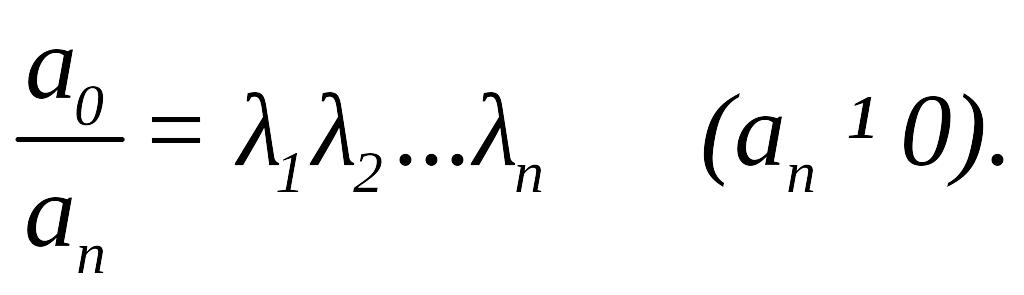 Якщо
,
то
.
Ця умова є необхiдною
умовою стiйкостi,
тому що змiна
знаку нерiвнiстi
свiдчить
про те, що модуль деяких коренiв
перебiльшує
одиничне значення. Але
i виконання цiєї нерiвнiстi не гарантує
знаходження всiх коренiв у областi
стiйкостi. Тому треба мати достатнiй
критерiй стiйкостi. Тодi для виразу
Якщо
,
то
.
Ця умова є необхiдною
умовою стiйкостi,
тому що змiна
знаку нерiвнiстi
свiдчить
про те, що модуль деяких коренiв
перебiльшує
одиничне значення. Але
i виконання цiєї нерiвнiстi не гарантує
знаходження всiх коренiв у областi
стiйкостi. Тому треба мати достатнiй
критерiй стiйкостi. Тодi для виразу
![]() утворюється друга дріб
утворюється друга дріб
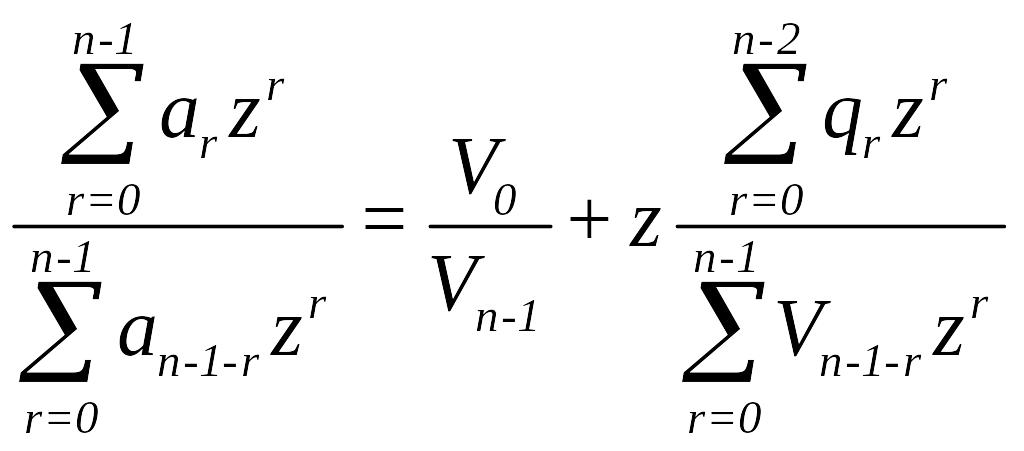 та перевіряється на відношення
та перевіряється на відношення
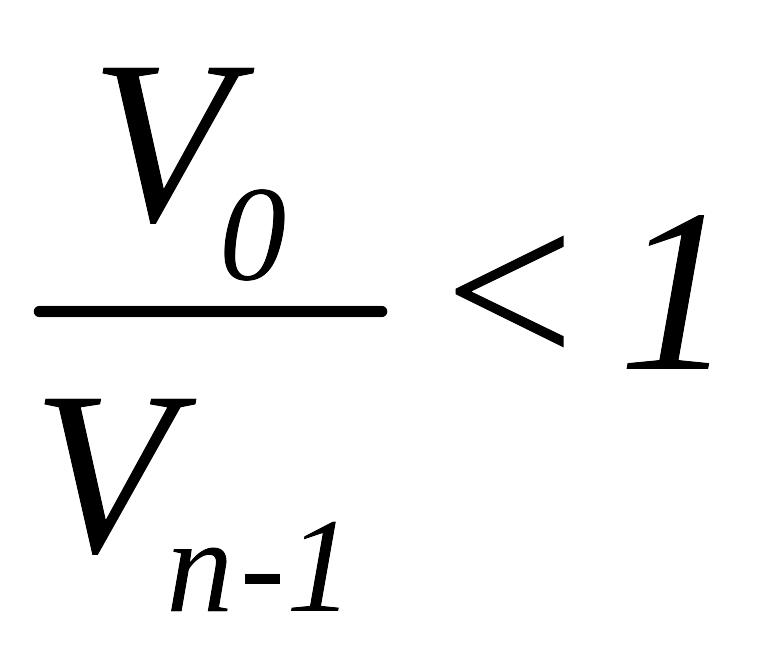 .
Цi процедури дiлення i перетворення
полiномiв остачі та видiлення окремого,
незалежного вiд z, продовжують до n крокiв.
.
Цi процедури дiлення i перетворення
полiномiв остачі та видiлення окремого,
незалежного вiд z, продовжують до n крокiв.
Якщо
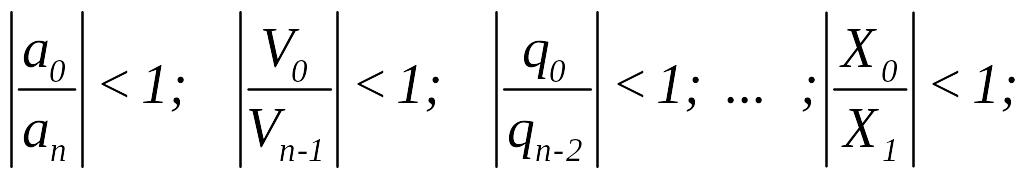 то система стiйка. Цей
критерiй визначення стiйкостi дискретних
систем запропоновано Е.Джурi.
то система стiйка. Цей
критерiй визначення стiйкостi дискретних
систем запропоновано Е.Джурi.
П 2.33
Визначити стійкість дискретної системи характеристичний поліном якої
![]()
1. Утворюється перша дріб та визначається перша остача
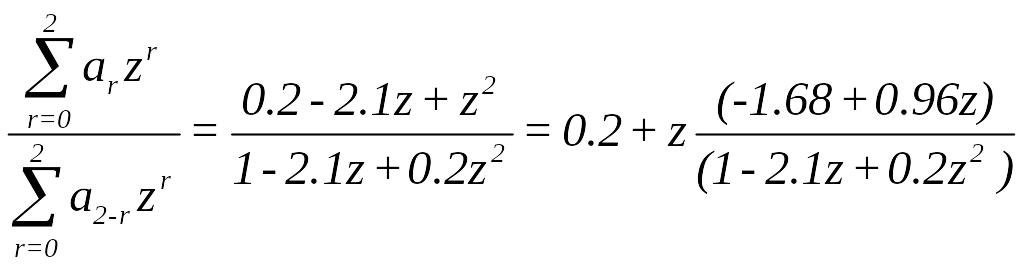
2. Утворюється друга дріб та визначається друга остача
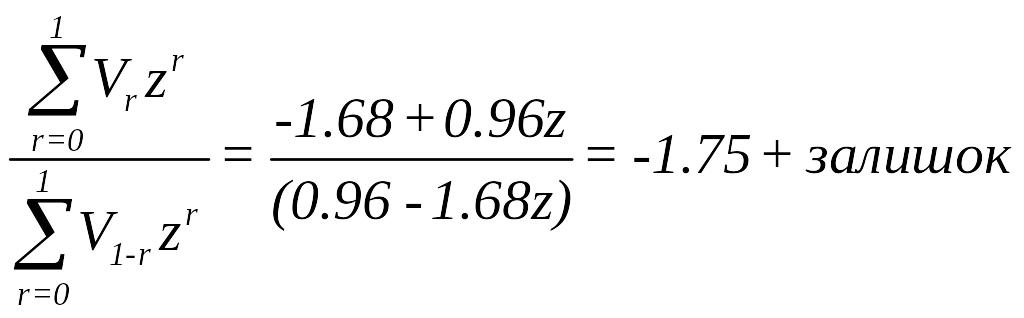
Отже,
система нестiйка, тому що
![]() .
.
Дiйсно,
тому що
![]() то
то
![]() .
.
2.7 Оцінка точностi роботи дискретних систем у сталих режимах
Для визначення точності дискретних САУ у сталих режимах використовують величину сталих похибок при рiзноманiтних типових впливах.
Хай задано замкнену ДСАУ з перериванням сигналу похибки (Рис.107).
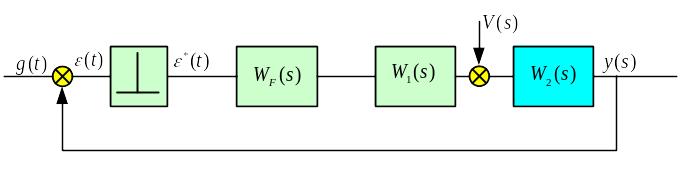
Рис. 107 Структурна схема дискретної системи
У
замкненій
дискретній
системі
з
одиничним
зворотним
зв'язком
похибка
системи![]() ,
задаючий
вплив
,
задаючий
вплив
![]() та
збуджуючий
вплив
v зв'язанi
вiдповiдним
рiвнянням
вiдносно
та
збуджуючий
вплив
v зв'язанi
вiдповiдним
рiвнянням
вiдносно
![]() -зображень
-зображень
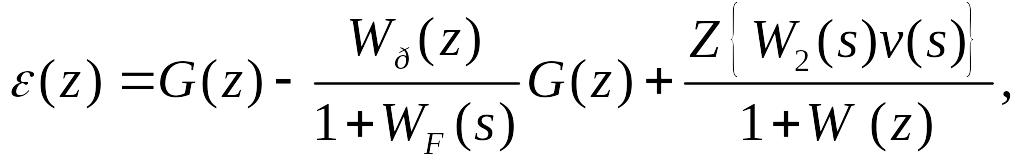
де
![]()
При цьому
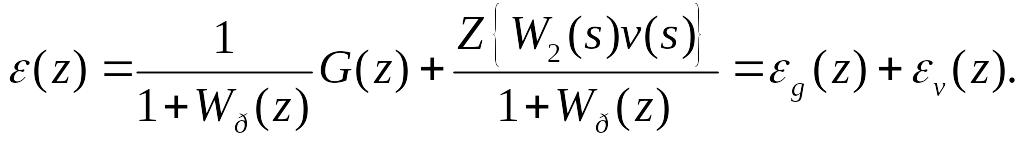
Здобутий
вираз має
-зображення
двох складових похибки, перша із яких
обумовлена задаючим впливом
,
а друга – збуджуючим впливом
![]() .
.
Стала похибка дискретної системи може бути обчислена за теоремою про кінцеве значення дискретної функції
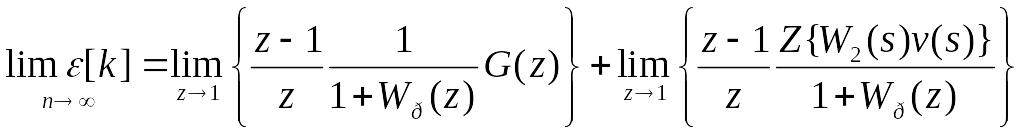 (114)
(114)
Якщо
на вхід системи подається ступінчата
функція
![]() зображення
якої
зображення
якої
![]()
а
збуджуючий вплив
дорівнює нулю, то стала похибка
![]() визначається за спiввiдношенням
визначається за спiввiдношенням
![]() (115)
(115)
i називається похибкою системи по положенню.
Якщо
вхідний вплив
![]() ,
то
,
то
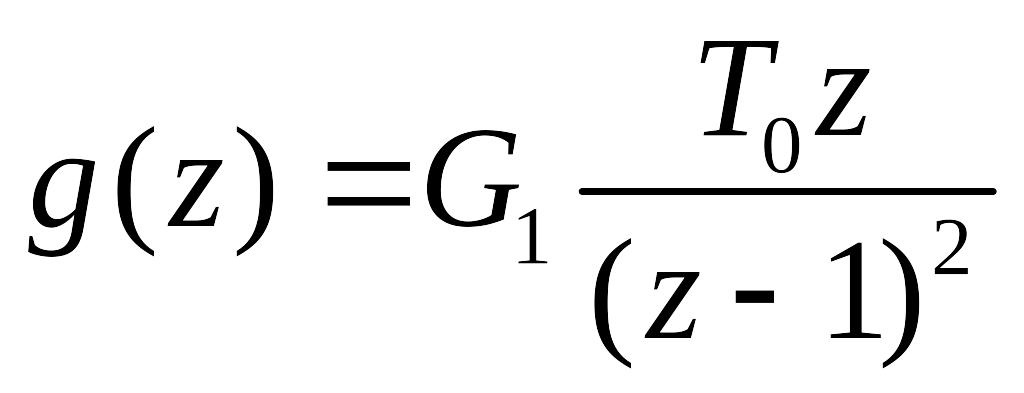 ,
а стала похибка визначається за
допомогою спiввiдношення
,
а стала похибка визначається за
допомогою спiввiдношення
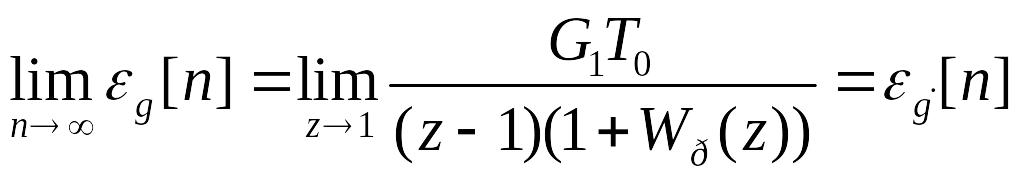 (116)
(116)
i називається похибкою системи за швидкістю.
Якщо
вхідний сигнал змінюється з постійним
прискоренням, тобто
![]() ,
зображення якого дорівнює
,
зображення якого дорівнює
![]() (117)
(117)
то стала похибка називається похибкою за прискоренням
![]() (118)
(118)
Дискретні
системи можуть класифікуватися у
вiдповiдностi з числом полюсів виразу
![]() при
при
![]() .
Якщо передаточна функція розімкненої
системи
.
Якщо передаточна функція розімкненої
системи
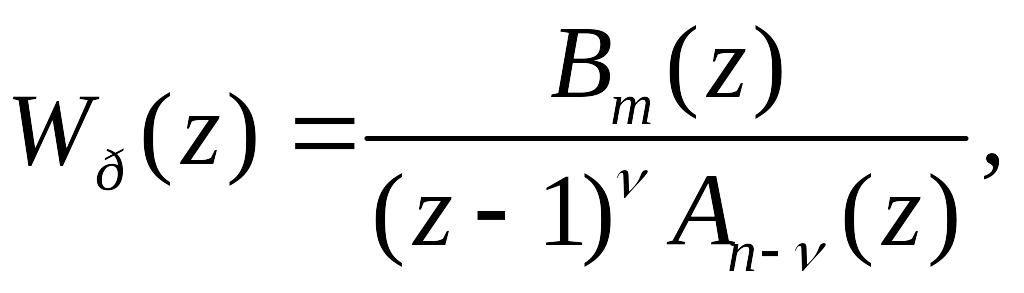 (119)
(119)
а
![]() не отримує полюсів
,
то при
не отримує полюсів
,
то при
![]() система буде статичною, при
система буде статичною, при
![]() астатичною першого порядку тощо.
астатичною першого порядку тощо.
Таким чином, для того щоб дискретна система мала нульову сталу похибку по задаючому впливу, необхідно, щоб порядок астатизму системи перевищував степінь поліному вхідного впливу.
Розклавши
передаточну функцію
![]() за сигналом похибки для задаючого впливу
у ряд по степеням
за сигналом похибки для задаючого впливу
у ряд по степеням
![]() ,
здобудемо
,
здобудемо![]() (120)
(120)
Коефiцiєнти
ряду
![]() ,
,
![]() ,
,
![]() ,...
називаються вiдповiдно коефiцiєнтами за
положенням, за швидкістю, за прискоренням.
При цьому
,...
називаються вiдповiдно коефiцiєнтами за
положенням, за швидкістю, за прискоренням.
При цьому
![]() ,
а
,
а
![]() визначає
повну сталу похибку, яка визначається
кількістю різностей у вхідному сигналі.
визначає
повну сталу похибку, яка визначається
кількістю різностей у вхідному сигналі.
При цьому
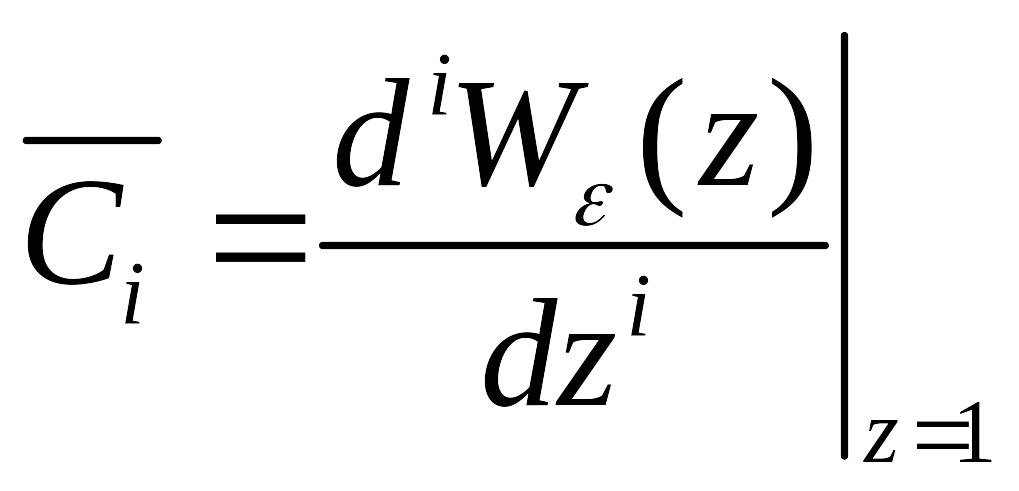 (121)
(121)
За аналогом з неперервними системами можна ввести поняття добротності за положенням, за швидкістю, за прискоренням
![]() (122)
(122)
При використанні білінійного перетворення для малих значень періоду квантування
![]()
можна
визначити коефiцiєнти похибки при
розкладі передаточної функції
![]() у ряд по степеням
.
Таким чином, при малих
справедливо рівняння
у ряд по степеням
.
Таким чином, при малих
справедливо рівняння
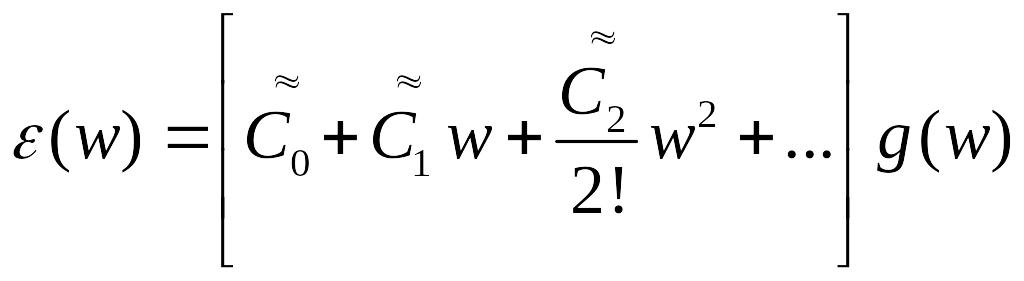 ,
де
,
де
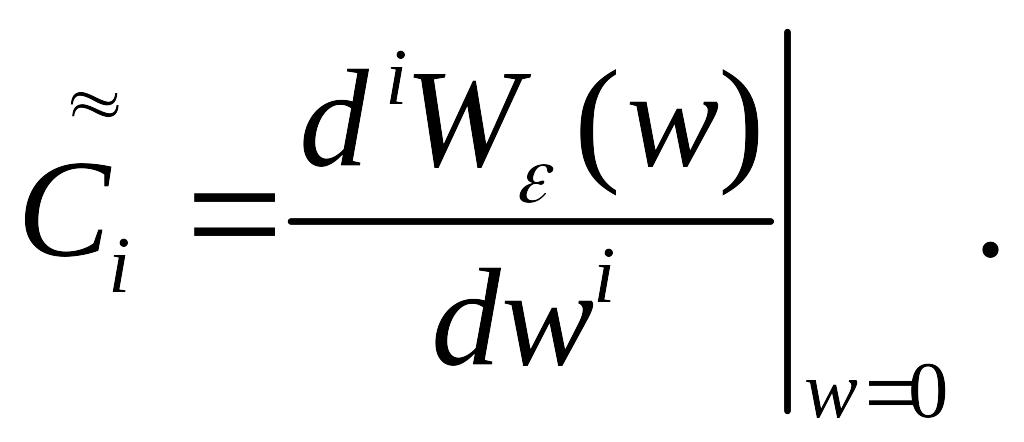 (123)
(123)
При
цьом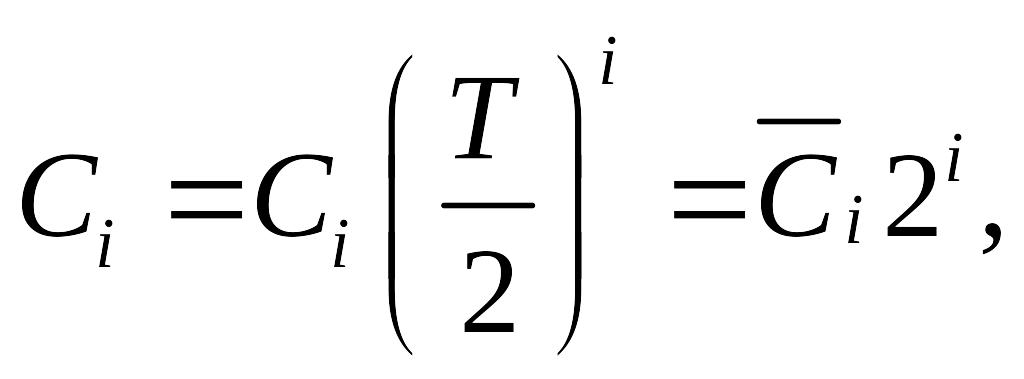 що відкриває можливість для знаходження
коефiцiєнтiв похибки по логарифмічним
характеристикам, які побудовані у
залежності від псевдочастоти
що відкриває можливість для знаходження
коефiцiєнтiв похибки по логарифмічним
характеристикам, які побудовані у
залежності від псевдочастоти
![]() .
.
Вимушена складова перехідної послідовності має вигляд
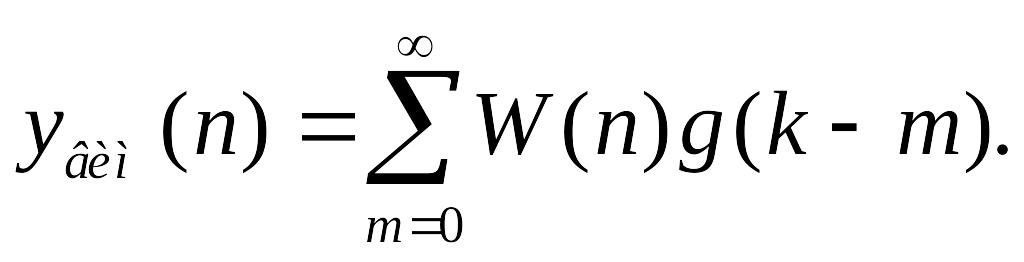
Якщо
![]() представити у вигляді розкладення
Тейлору
представити у вигляді розкладення
Тейлору
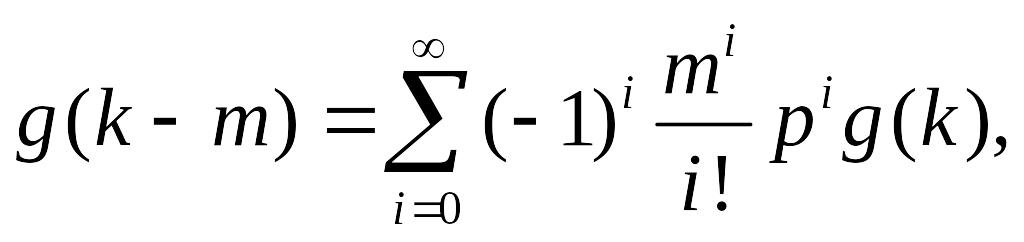 де
де
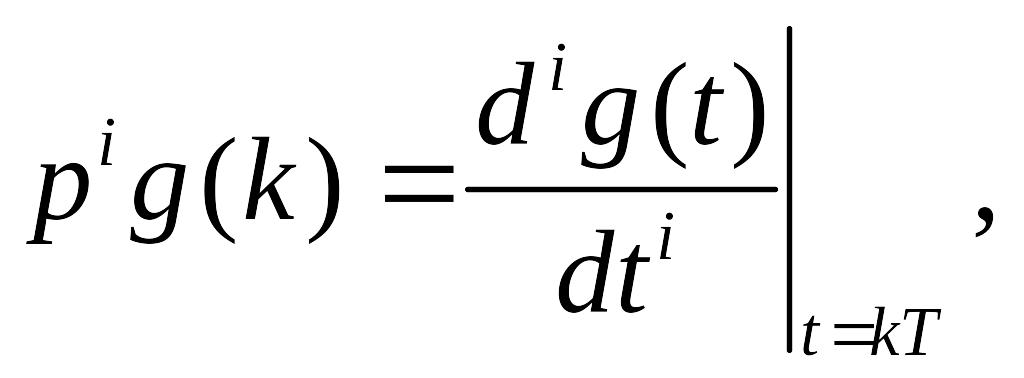 то
то
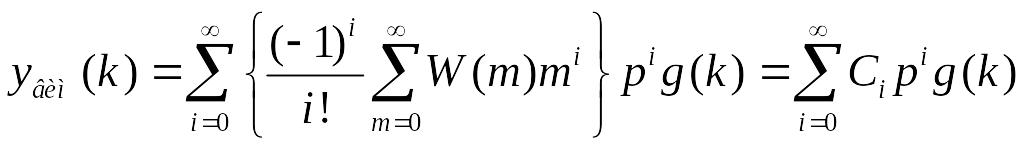 ,де
,де
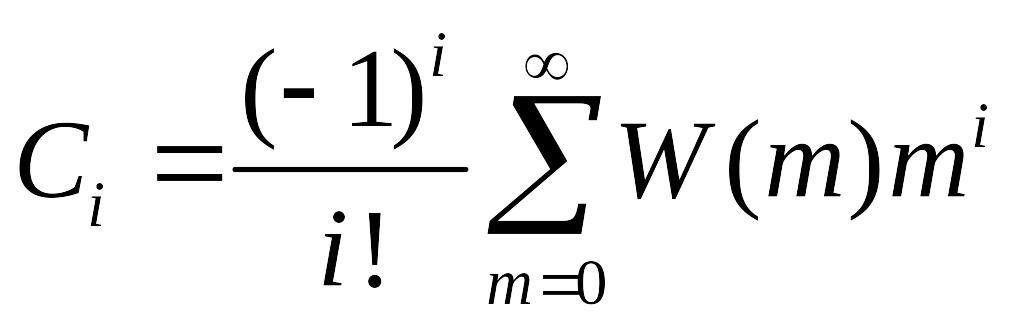 є також коефiцiєнтами похибки.
є також коефiцiєнтами похибки.
Якщо
на вхiд дискретної САУ поступає
моногармонiчний вплив
![]() ,
дискретна функцiя якого має вигляд
,
дискретна функцiя якого має вигляд![]() ,
то на виходi системи з'являється
послiдовнiсть
,
то на виходi системи з'являється
послiдовнiсть
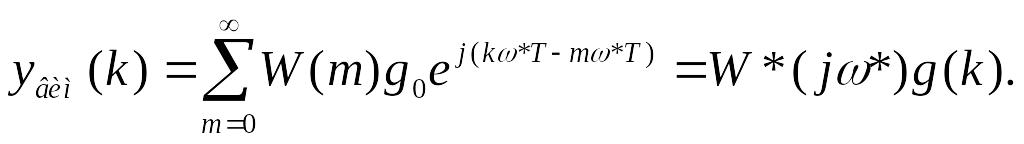
Якщо
частота вхiдного впливу дорiвнює частотi
квантування, то очевидно, що дискретна
функцiя вимушеної складової вихідної
величини буде сталою та буде залежити
від
g0
та
![]()
Аналогiчний висновок буде i для визначення вимушеної похибки
![]()
При цьому
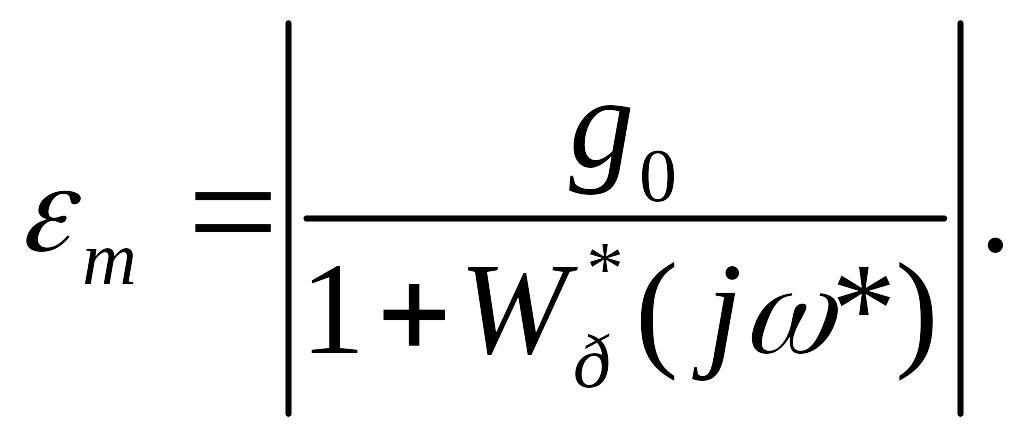 (124)
(124)
Якщо
![]() ,
то
,
то
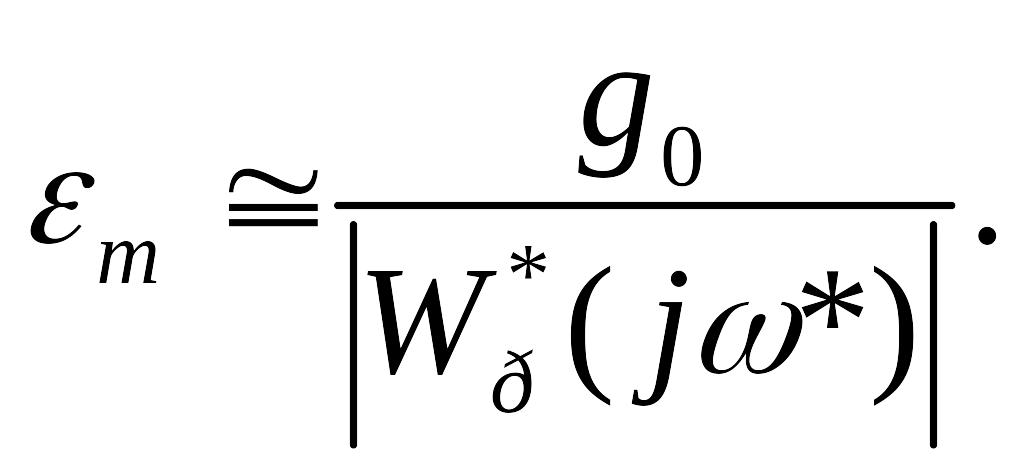 (125)
(125)
