2.6 Умови стійкості дискретних систем керування.

Дослiдження стiйкостi дискретних систем автоматичного управлiння базується на аналiзi стiйкостi рiшень системи лiнiйних дискретних рiвнянь, якi описують її динаміку. Ця система у загальному виглядi має вигляд

(102)

Система вважається стiйкою, якщо стiйке тривіальне рiшення відповідної однорідної системи .

Положення рiвноваги називається стiйким за Ляпуновим, якщо для будь-якого знайдеться таке що довiльна траєкторія, початкова точка якої лежить у -округи початку координат, , не покидає -округи початку координат при усiх додатних значеннях дискретного часу .

Система вважається асимптотично стiйкою, якщо виконуються умови

(103)

Хай є скалярна функцiя , яка однозначна та неперервна по , знаковозначна . Якщо виконуються умови (104), то функцiя є функцiєю Ляпунова, а система управлiння вважається стiйкою.

Тому що рiшення дискретного рiвняння вiдшукується у виглядi , де вiльна складова, яка є рiшенням однорiдного рівняння

та дорiвнює 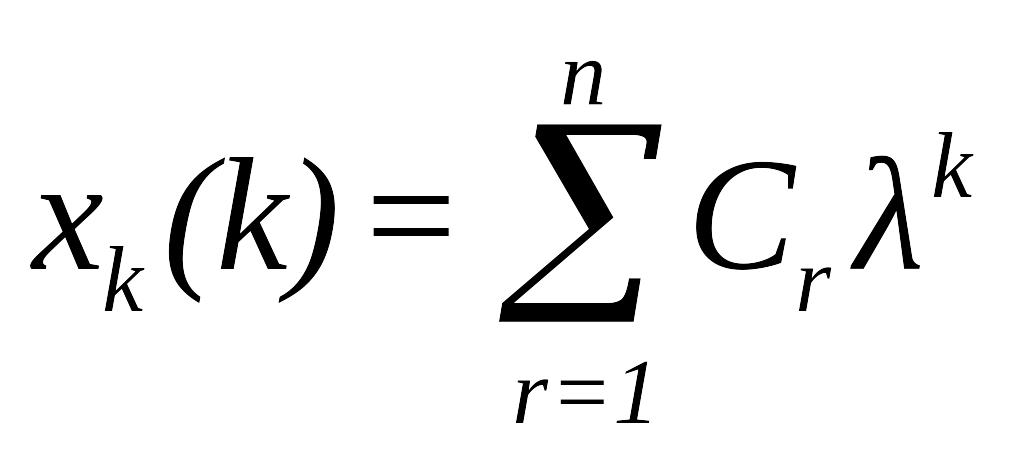, де є коренями характеристичного рівняння тобто , то X(k) стiйке, якщо для будь-яких коренiв виконуються умови

(105)

При цьому, якщо є дiйсними та додатними, то процес згасає монотонно; якщо вiд'ємнi або комплексно-сполученi, то процес буде згасаючим коливальним, а процес згасає тим швидше, чим менша дiйсна частина кореня. У випадку процес згасає за один крок (Рис.49). Таким чином для дослiдження стiйкостi дискретної системи треба встановити факт Ця умова вважається необхiдною та достатньою.

Хай вiльний рух системи описується рiвнянням

Побудуємо квадратичну форму

(106)

де N-квадратична симетрична матриця та визначимо першу рiзницю

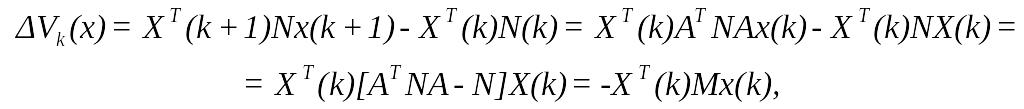
де (107) є матричним рiвнянням Ляпунова .

Рис.106 Вплив полюса на вигляд перехідного процесу

Вiдомо, що якщо вiдповiднi значення матрицi задовольняють умови то симетрична матриця однозначно визначається iз матричного рiвняння Ляпунова за симетричною матрицею .

Тому що для стійкої системи , то спiввiдношення (54) повинно виконуватися, а отже додатно-визначенiй матрицi вiдповiдає єдина симетрична матриця , яка буде також додатно-визначеною.

Отже, квадратична форма є функцiєю Ляпунова для граничної системи та відповідає умова

при

при

Областю визначення цiєї функцiї буде весь простiр стану

2.6.1 Алгебраїчні критерії стійкості дискретних систем. Критерій гурвіця.

Для використання алгебраїчного критерiю Гурвиця для дослідження стійкості дискретних систем необхiдно вiдобразити одиничне коло, яке утримує коренi характеристичного рiвняння A(z) = 0 замкненої системи за допомогою дрiбно-лiнiйного перетворення на лiву півплощину комплексної змiнної . При цьому коло одиничного радiусу у площинi перетворюється у уявну вiсь площини , яка є межею областi стiйкостi.

Отже, многочлен записується у виглядi

(108)

i, пiсля зведення коефiцiєнтiв при однакових степенях w, зводиться до вигляду А(w), до якого застосовується критерiй Гурвiця з всiма правилами неперервних систем.

Якщо записується у виглядi

(109)

то для використання найбiльш поширеного алгебраїчного критерію - критерію Гурвiця необхiдно по коефiцiєнтам многочлена скласти визначник Гурвiця, який записується у формi

(110)

Правило його складання просте та легко запам'ятовується :

за порядком, починаючи з a_k-1 виписуються по дiагоналi усі коефiцiєнти, а потiм заповнюються строки у порядку збiльшення iндексiв у право та зменшення - влiво. Коефiцiєнти з iндексами, якi перевищують або менше нулю, замiнюються нулями.

Для виконання необхiдних умов стiйкостi повиннi виконуватися умови :

всi коефiцiєнти а_i повиннi бути бiльше нулю . Тодi достатнiми умовами стiйкостi тобто факт визначення, що коренi многочлена належать лівій півплощині, тобто , є умови

(111)

тобто всi визначники Гурвiця повиннi бути додатними числами.

Тому що визначник , а , то очевидно, що знак визначника визначається знаком визначника .

При цьому можна обмежитись умовам .

П 2.32

Визначити стійкість дискретної системи, якщо задана передаточна функція та її параметри

1. Визначається передаточна функція замкнутої системи

Визначається характеристичне рівняння та виконується перехід до W-перетворення

Визначаються визначники Гурвіця

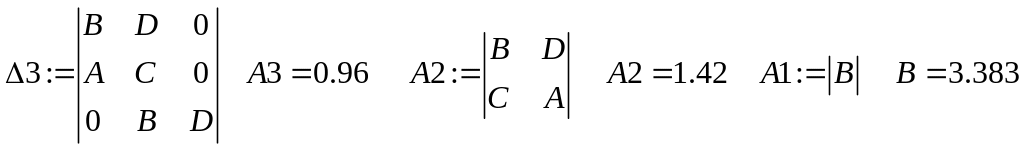
Висновок: Всі визначники більше нуля. Система стійка.