2.5.2 Передаточка функція умовно розімкнутої дискретної системи

Розглянемо послiдовне з'єднання імпульсного елементу та неперервної частини W_нч(s). Тому що імпульсний елемент можна представити у виглядi iдеального iмпульсного квантування та формуючої ланки W_ф(s), то послiдовне з'єднання W_ф(s) з W_нч(s) утворює приведену передаточну функцiю W_пнч(s).

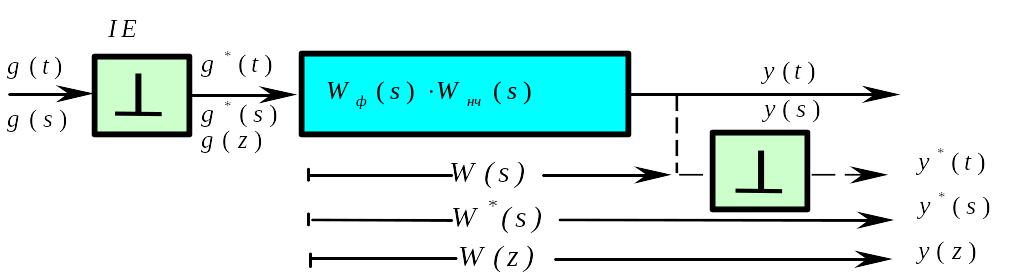
Рис. 92 Розімкнутий канал дискретної системи

Очевидно, що

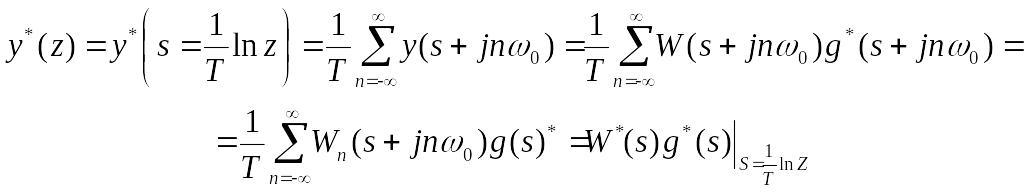
Очевидно також, що

Таким чином,

де (92)

Якщо узагальнювати цей висновок, то :

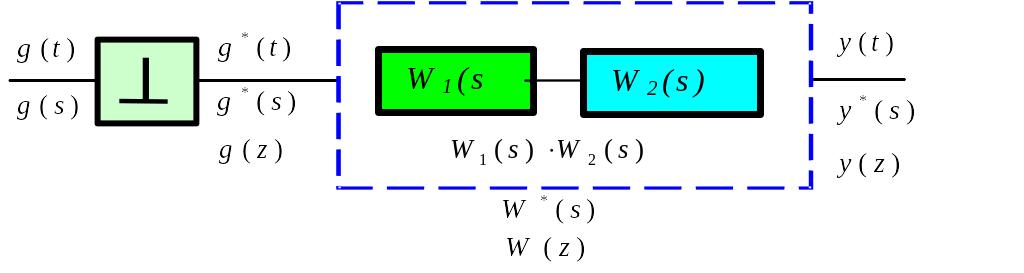
Рис. 92 До виводу передаточної функції розімкнутої системи

Передаточна функцiя послiдовно з'єднаних лано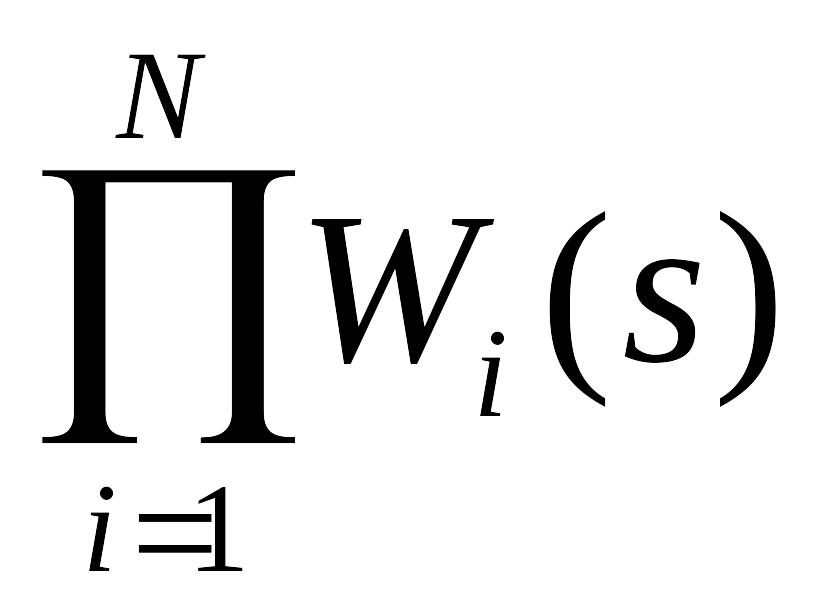к дорiвнює Z-перетворенню добутку передаточних функцiй цих ланок 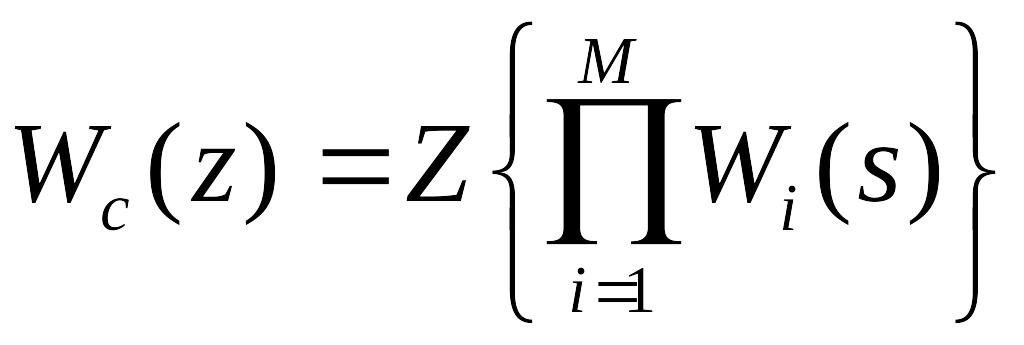. Якщо перед кожною ланкою буде виконуватись квантування (Рис.93), визначення узагальненої передаточної функцiї буде виконуватись за схемою.

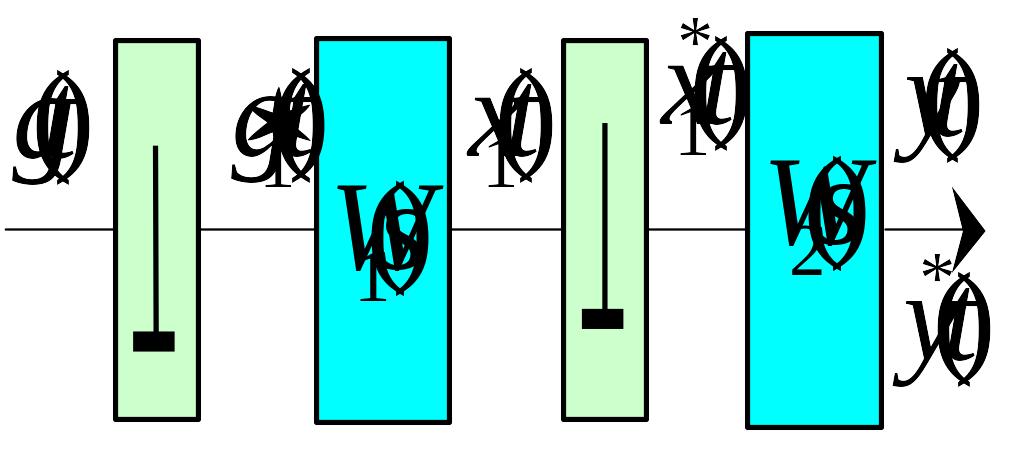
Рис. 93 До виводу передаточної функції розімкнутої системи при умовах постановки імпульсного елемента на входах неперервних ланок

. (93)

Хай

Тодi

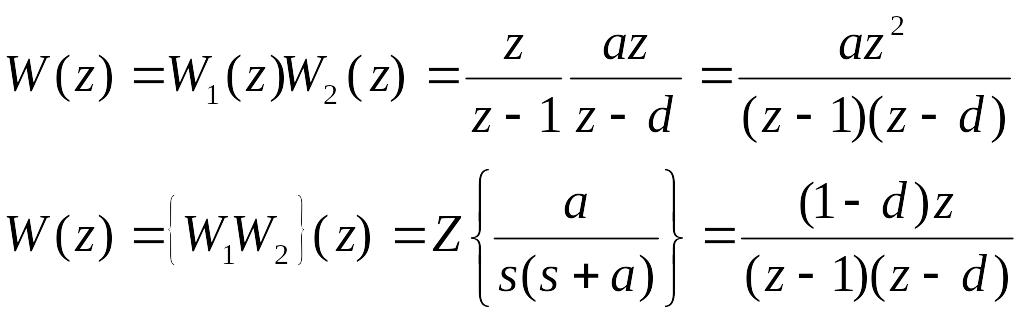
Якщо розглядати послiдовне з'єднання передаточних функцiй мiж якими є iмпульсний елемент (Рис.94), то узагальнена передаточна функцiя не може бути визначена.

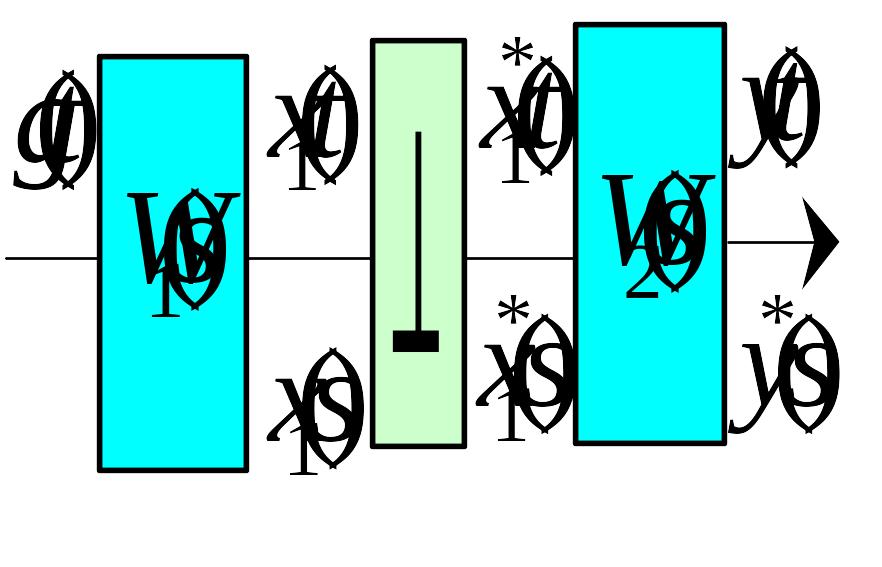
Рис.94 Послiдовне з'єднання передаточних функцiй мiж якими є iмпульсний елемент

Дiйсно, тому що то

Отже,

(93)

2.5.3 Передаточнi функцiї замкнених дискретних систем

Розглянемо замкнену систему з квантуванням сигналу похибки (Рис.95).

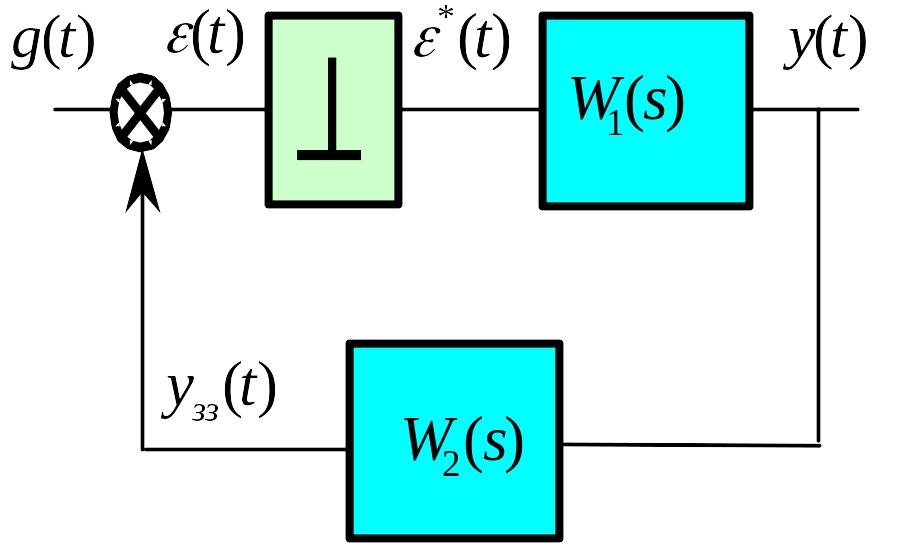
Рис.95 До визначення передаточної функції замкнутої системи з імпульсним елементом у прямому каналі

Тому що W_р(s)={W₁W₂}^*(s),

то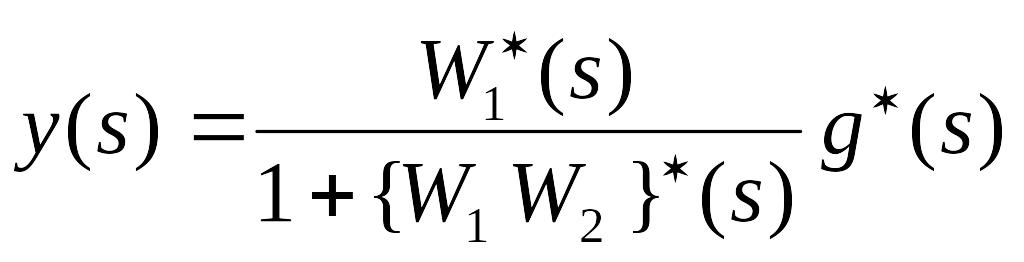

Отже, 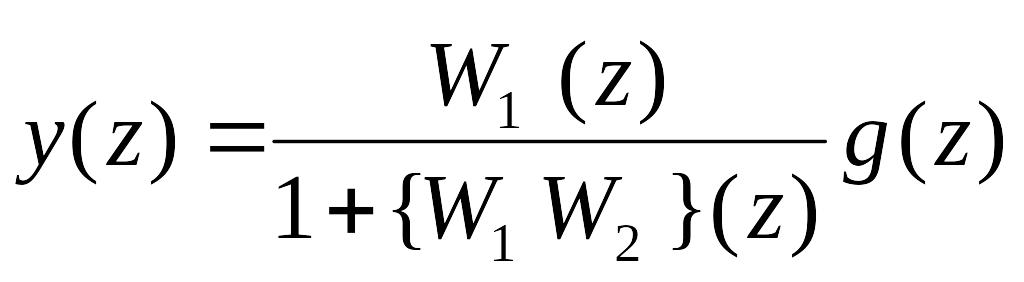(94)

Якщо квантування виконується i у загальному зв’язку (Рис.96), то

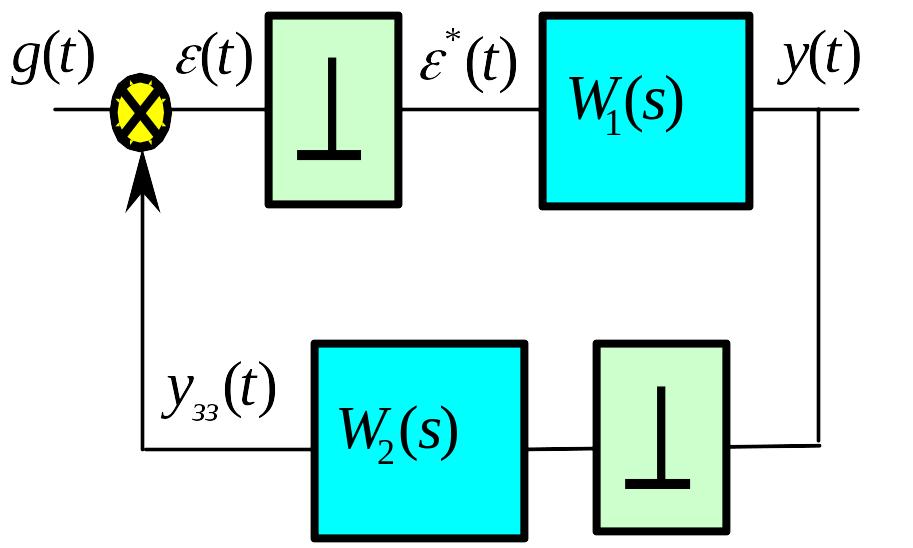
Рис. 96 До визначення передаточної функції замкнутої системи з імпульсними елементами у прямому та зворотному каналах

(95)

Очевидно, що для випадку (Рис.97), передаточна функцiя не може бути визначена

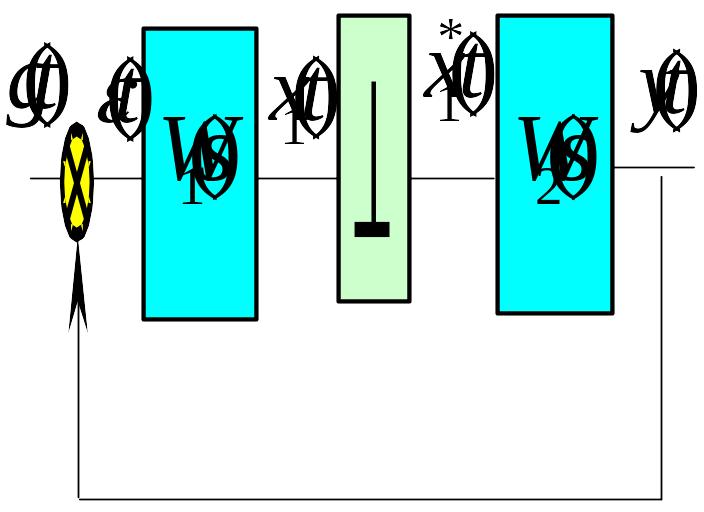
Рис. 97 Приклад, коли передаточна функція не може бути визначена

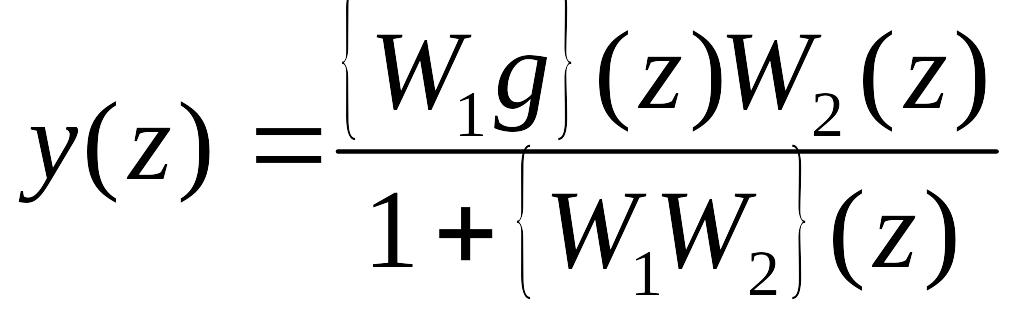(96)

П 2.25

Скласти загальне дискретне рівняння для дискретної системи 1–ог порядку

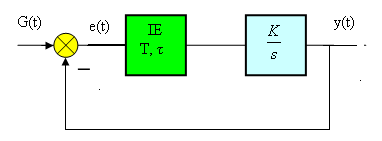
якщо імпульсний елемент - фіксатор нульового порядку .

1. Визначається дискретне рівняння

2. Розвязок має вигляд

Характеристичне рівняння

Умова закінчення перехідного процесу за мінімальницїй час .

Отже,

3. Визначається дискретне рівняння відносно передаточних функцій

Передаточна функція неперервной частини

Передаточна функція ФНП

Передаточна функція умовно-розімкнутої системи у Z-формі

Передаточна функція замкнутої системи

Дискретне рівняння

3. Визначається розв’язок дискретного рівняння та вплив коефіцієнта підсилювання на якість перехідних процесів

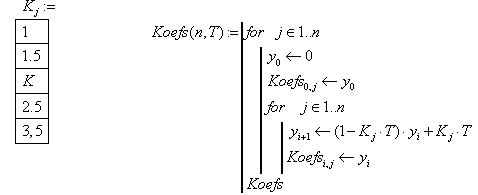
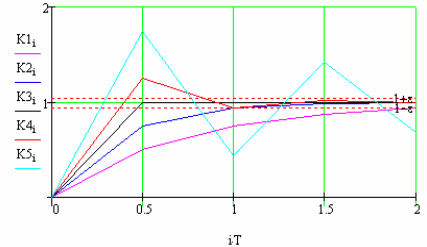
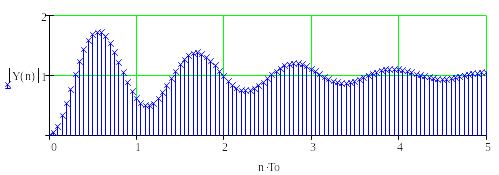
Рис. 98 Залежність перехідної характеристики від коефіцієнту підсилювання

Визначається розв’язок дискретного рівняння та вплив періоду квантування на якість перехідних процесів.

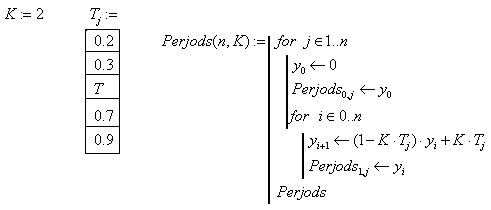
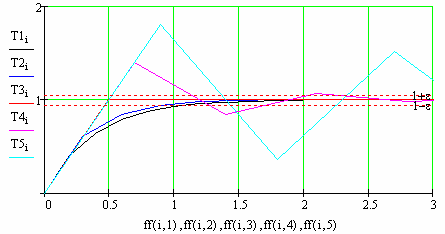
Рис. 99 Залежність перехідної характеристики від періоду квантування

П 2.26

Скласти загальне дискретне рівняння відносно Z –перетворення для дискретної системи 2 –ог порядку ( варіант А, В, С )

A.

B.

C.

П 2.27

Розв’язати дискретне рівняння

1. Розв’язок здобувається у вигляді

Початкові умови

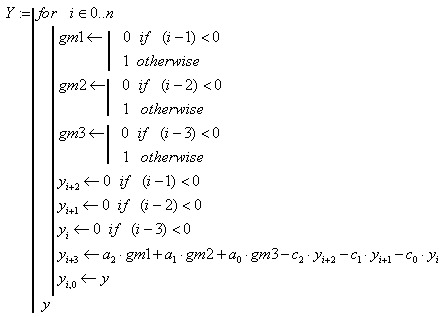
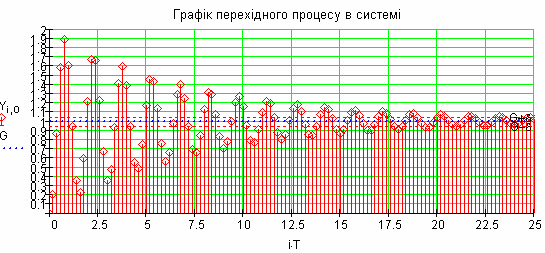
Рис. 100 Перехідний процес до П

П 2.28

Розрахувати перехідні процеси у дискретної системи

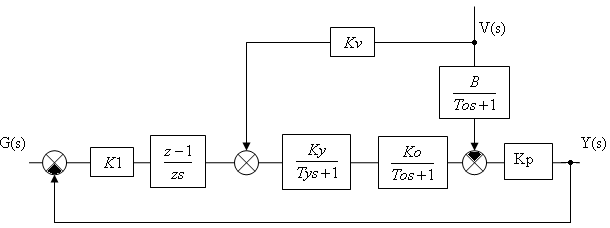
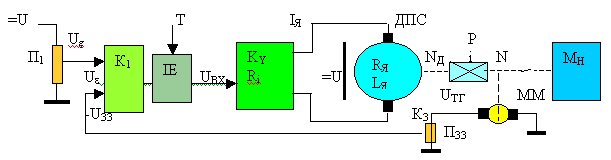
Рис. 101 Структурна схема дискретної системи замкнутого керування

1. Визначаються передаточні функції

Передаточна функція умовно розімкнутої системи

Передаточна функція замкнутої системи

2. Досліджується вихід у робочу точку

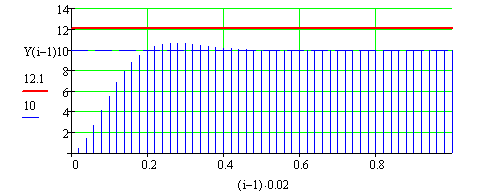
Рис. 102 Вихід у робочу точку

3. Досліджується вплив навантаження

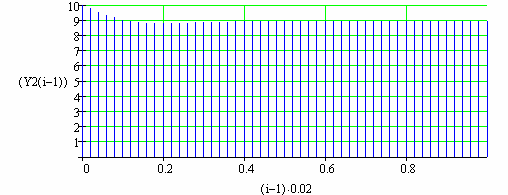
_{Рис.103 Вплив навантаження}

4. Досліджується можливість компенсації навантаження

Коефіцієнт передачі каналу компенсації (статичний)

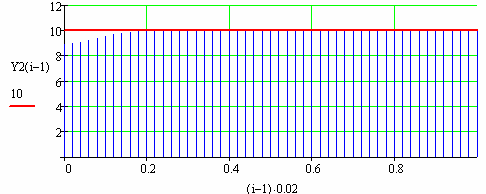
Рис.104 Компенсація впливу навантаження

П 2.29

Для дискретної системи 2-го порядку з фіксатором нульового порядку скласти математичну модель у Z-формі

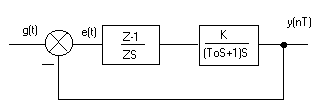
- одинична функція Хевісайда

Зображення сигналу на виході системи

Передаточна функція умовно розімкнутої системи у S-формі

Передаточна функція замкнутої системи

П 2.29

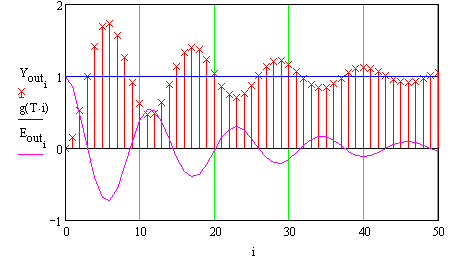
Для умов задачі П 2.28 розрахувати перехідний процес

При заміні

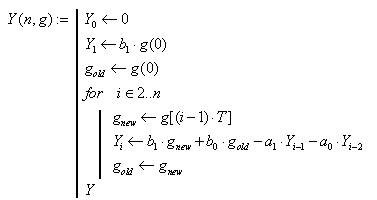
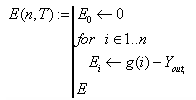
П 2.30

Для умом задачі П 2.29 визначити прямі показники якості перехідного процесу

Величина пере регулювання

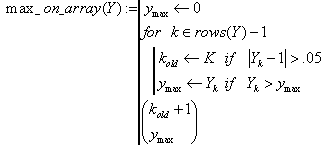
2.5.4 Передаточна функці каналу АЦП-ЦОМ-ЦАП

Вхідні та вихідні перетворювачі мають статичні характеристики ступінчатого вигляду. Для подібних характеристик тангенс кута похилу або дорівнює нулю, або наближається до нескінченності. Тому для вхідних та вихідних перетворювачей використовується метод лінеаризації, який основан на припущенні, що зміна вхідного сигналу по своєї величинє значно більше молодшого розряду перетворювача, тобто можна зневажати впливом ступенчатості характеристики та лінеаризовати її проводячі деяку середню пряму (Рис. ).

По осі абцис відкладається неперервне значення задаючого впливу , а по осі ординат – його цифрове представлення (число) , яке здобувається на виході вхідного перетворювача у десятичної системі числення.. При цьому величина молодшого розряду на вході позначається як та має фізичну розмірність, яка співпадає із розмірністю задаючого впливу. В цому разі одиниця молодшого розряду на виході перетворювача дорівнює безрозмірної одиниці. Якщо припустити, що тривалість горизонтальних площадок однакова та дорівнює одиниці молодшого розряду , то для характеристики буде існувати залежність

, (97)

де - ціла частина числа у квадратних дужках. Тоді для лінеаризованої характеристики ( штрихова лінія) коефіцієнт передачі (98) і, отже, найбільша похибка не буде перевищувати по модулю значення . Число рівнів, яке відрізняється від нуля на однієї гілки характеристики дорівнює ,(99), де число дроїчних розрядів перетворювача без урахування знакорого розряду.

Аналогічно розглядається і перетворювач керованої величини та його цифрове представлення . Якщо одиниця молодшого розряду представити як , по похил лінеаризованої характеристики буде , а число рівнів характеристики .(100). Звичайно використовуються перетворювачї з та .

Так, наприклад, якщо необхідно вимірюрати кут повароту якой небудь осі з похибкоб не більше , то одиниця молодшого розряду повинна бути обраною з умов . Тоді для забезпечення вимірювань у межах число розрядів повинно бути

.

Якщо задачею систнїеми керування є забезпечання рівності ( слідкуюча система) , то , то для перетворення можна використовувати сигнал похибки .

Тому що на виході цифрового обчислювача зявляється цифрове число, а керуючий вплив як правило представляється у вигляді фізичного сигналу, то необхідно виконувати перетворення цифрового слора у аналоговий сигнал відповідної розмірності (ЦАП). Якщо позначити одиницю молодшого розряду вихідної величини як , а одиницю молодшого розряду вхідної величини як бізрозмірну одиницю, то їх відношення визначить похил лінеаризованої характеристики з . При цьому .

Якщо у цифровому обчислювачу для сталих режимів є пряма пропорціїність чисел на вході ті виході, тобто , то обчислювач можна розглядати як статичну ланку з коефіцієнтом передачі . При цьому загальний коефіцієнт передачі буде

. (101)

Структурна схема цифроваї системи може бути представлена у вигляді

Рис .105 До визначення передаточної функції цифрової системи керування

Розглянемо так звану зведену вагову функцію w_П(t) неперервної частини сумісно з ексраполятором(фільтром W_Ф(s). тобто реакцію наодиничну імпульсну функцію . Неперервна частина сумісно з екстраполятором розглядається як деякий імпульсний фільтр, який характеризуєтьчя решітчастою функцією ваги w_П(n). Зображення на фиході буде мати вигляд

Y₀ (z) = Z{y(n)} = Z{w_П(n)} ,

а передаточна функція W₀(z)=y₀(z)/x₀^*(z)=Z{w(n)} або W₀(z) = Z{W_Ф(s)W_Н(s)}.

Передаточна функція ЦКП визначається відношенням зображень вихідної величини до зображення вхіжної при нульових початкових умовах

D(z) = X(z)E^-1(z) =(b₀z^m + b₁z^m-1+…+b_m-1z+b_m)(a_oz^k +a₁z^k-1+ …+a_n-1z + a_n)^-1.

Для умов фізичної можливості не рекурсивного фільтру повинні виконуватися умови . Якщо представити передаточну функцію у вигляді

D(z)=(b₀ + b₁z^-1+…+b_k-1z^-(k-1)+b_kz^-k)/(a_o +a₁z^-1 +…+a_k-1z^{-( k-1)} + a_kz^-k)^-1

При a_o=1 можна визначити лінійний алгоритм роботи ЦКП

X₀[n] = b₀e[n] + b₁e[n-1] + …+ b_ke[n-k] –

-( a₁x₀[n-1] +a₂x₀[n-2] +…+ a_kx₀[n-k]

П 2.31

Передаточна функція неперервної частини ЦСАК ,

Визначити передаточну функцію умовно – розімкнутої ЦСАК з пропорційним цифровим регулятором ( значення молодшого розряду АЦП , значення молодшого розряду ЦАП ,

_{Передаточна функція умовно – розімкнутої ЦСАК має вигляд}

_{Розрахунок виконувати з точністю до 4-х знаків}

1. _{Формуються вхідні данні:}

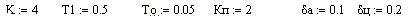
2. _{Визначається коефіцієнт передачі ЦР}

3. _{Визначається приведена передаточна функція неперерваної частини}

4. _{Визначається часова характеристика}

5. _{Визначається Z-перетворення з урахуванням періоду квантування}

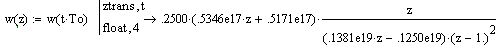
6. _{Визначається передаточна функція умовно – розімкнутої ЦСАК}

7. _{Визначається передаточна функція замкнутої ЦСАК}