2.5 Передаточні функції дискретних систем керування.

Розглянемо послідовне з’єднання ідеального імпульсного елемента та неперервної частини, яка задана своєю передаточною функцією W(s) (Рис.89) або функцією ваги W(t).

Рис.89 Ідеальний імпульсний елемент та неперервна передаточна функція

Будемо вважати, що при деякому .

Дискретне значення Y*(t)=Y(kT) можна визначити за допомогою імпульсного елемента, аналогічного імпульсному елемента на вході системи.

В цьому випадку .

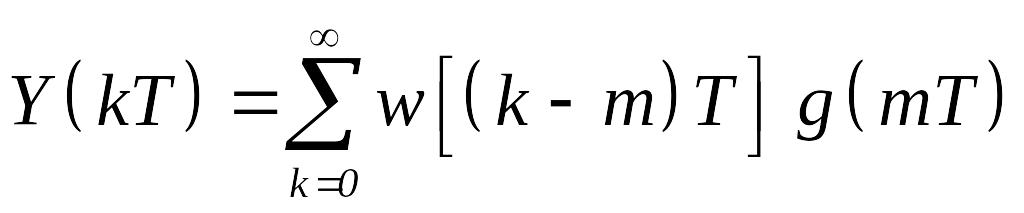Тому що , то

Зробимо підстановку при k = 0, n = -m.

Тоді .

Знайдемо перетворення Лапласа цієї послідовності

де є дискретною передаточною функцією

. (85)

Якщо покласти , то вираз

. (86)

визначає комплексний коефіцієнт передачі розімкненої дискретної системи і є спектром сигналу , який можна представити як результат пропускання сигналу , який дорівнює ваговій функції приведеної неперервної частини через найпростішу імпульсну ланку.

Процес перетворення неперервного сигналу у часовий фізичний імпульс при амплітудній модуляції може бути зображений наступним чином (Рис.90).

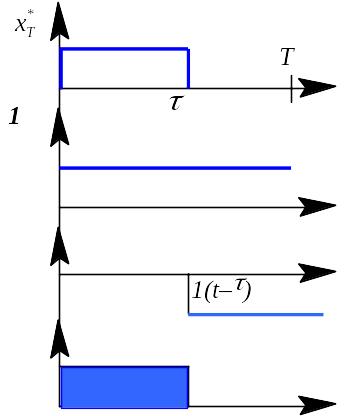
Рис. 90 До визначення передаточної функції імпульсного елементу

Із неперервного сигналу у момент перемикачем миттєвої дії вибирається значення сигналу який подається на запам’ятовуючий пристрій, та зберігається на його виході протягом часу .

Якщо зобразити цей імпульс як результат дії двох протилежних за знаком ступінчатих впливів та ,то в цьому випадку передаточну функцію імпульсного елементу можна визначити як або Тому що у цифрових елементах управління виконується запам'ятання значення імпульсу на весь період квантування, то , бо . Отже, передаточна функція в цьому випадку буде

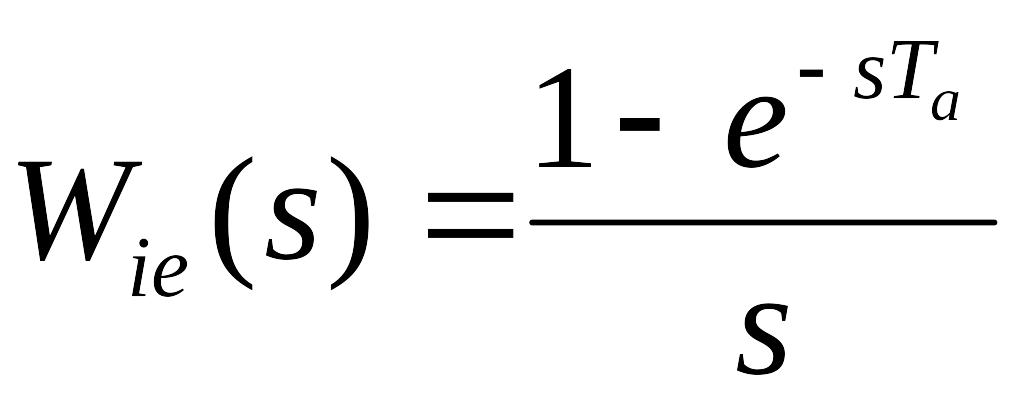(87)

Цій передаточній функції відповідає амплітудно-фазова характеристика

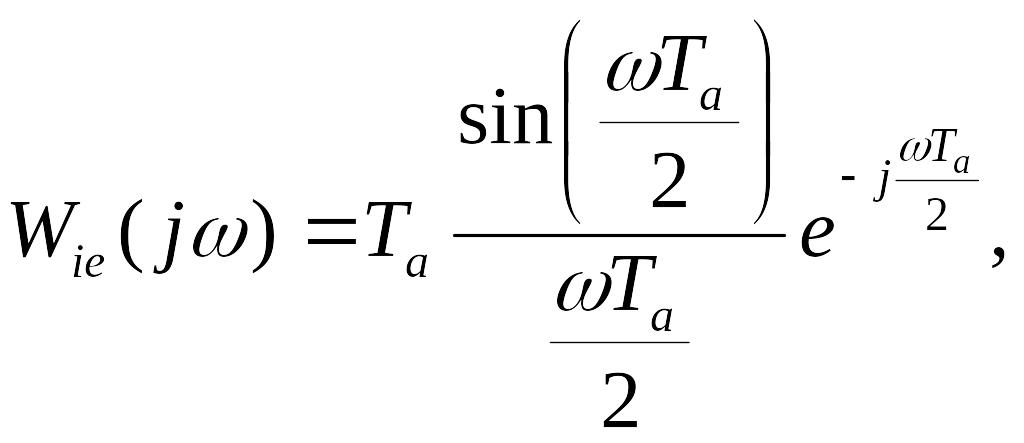яка показує, що затримка фази відповідає часу, який дорівнює половині періоду опиту.

2.5.1 Властивостi w(z)

Якщо використати теорему про кiнцеве значення дискретної функцiї, то можна визначити коефiцiєнти пiдсилювання дискретної системи.

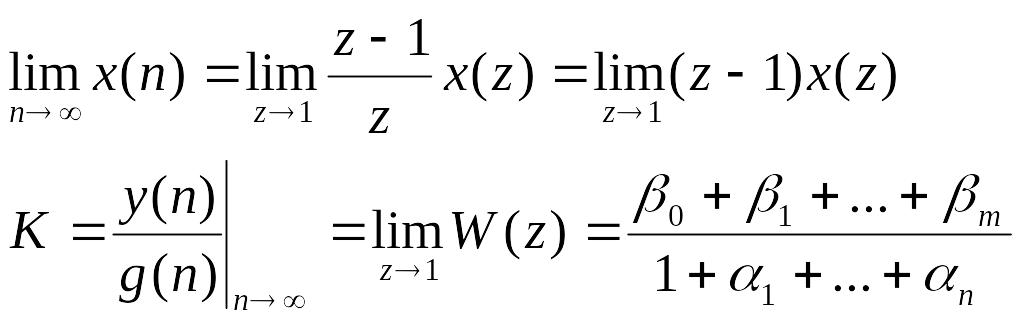(88)

Розглянемо iмпульсний елемент, який послiдовно з’єднано з неперервною частиною (Рис.91). Вiдомо, що об'єднання передаточних функцiй формуючої частини iмпульсного елементу з неперервною частиною системи визначає приведену передаточну функцiю

(89)

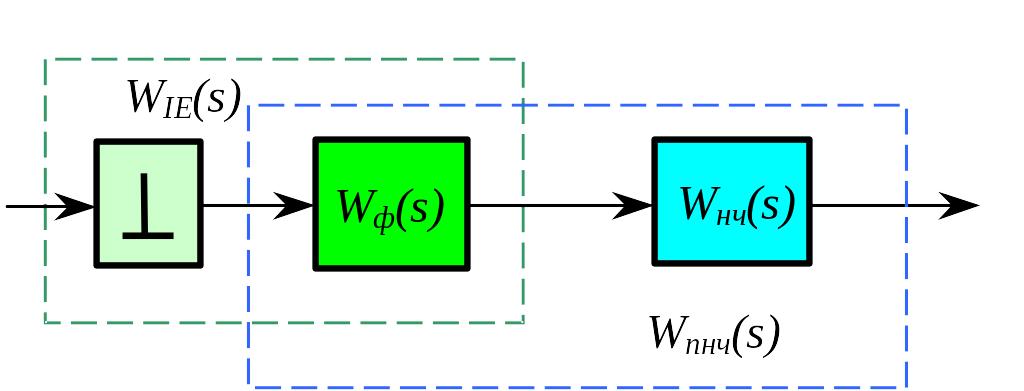
Рис.91 Приведен передаточна функція дискретної системи

Як було показано вище, передаточна функцiя амплiтудного квантування при має вигляд 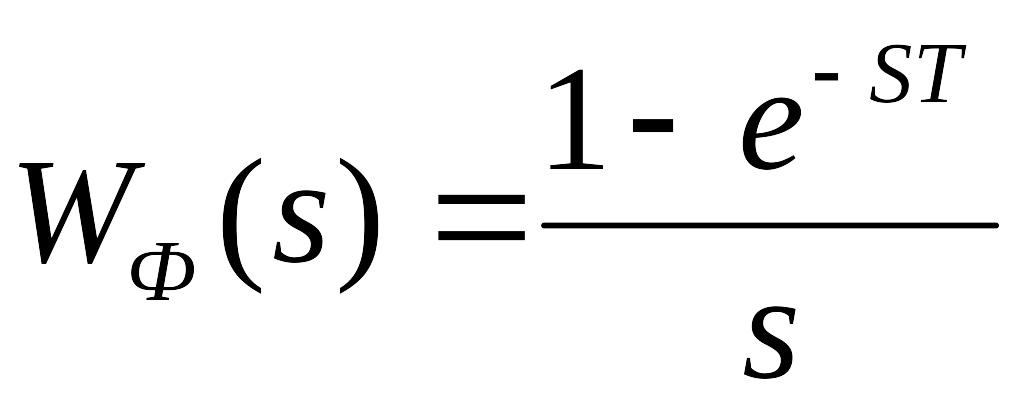Отже, зображення приведеної передаточної функцiї, тобто передаточної функцiї умовно розiмкненої системи визначається як

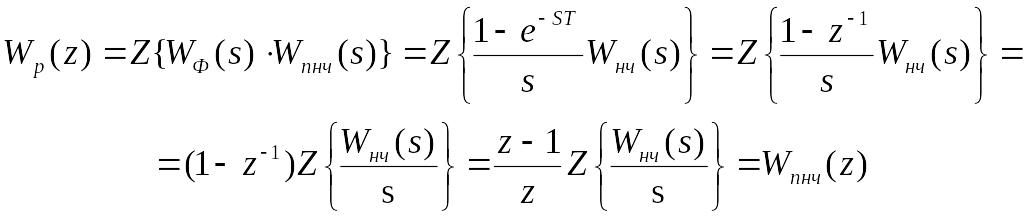(90)

Хай

Тодi

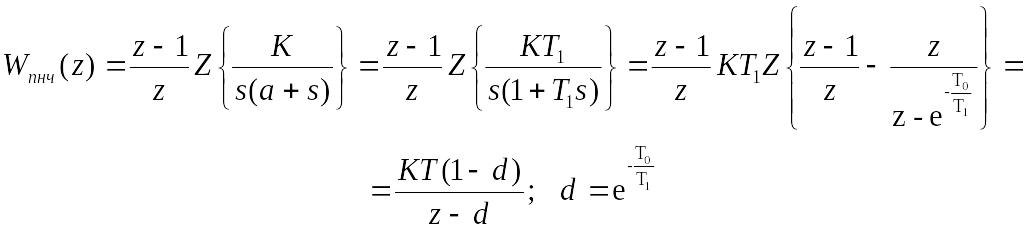
Якщо визначити передаточну функцiю тiльки одного iмпульсного елементу, то

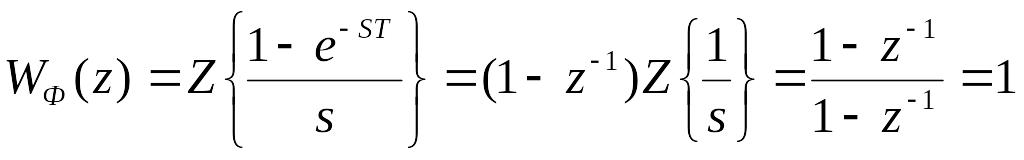(91)

Цей результат очевидний, тому що фiксатор нульового порядку протягом перiоду квантування утримує сталий дискретний сигнал, який добувається у результатi вибiрки, i обчислення Z-перетворення повинно визначити початковий квантований сигнал.