2.1.1 Складання дискретних рівнянь лінійних систем

Методику складання дискретних рівнянь розглянемо відносно умови функціонування дискретних систем автоматичного управління. Замкнення системи виконується тільки у моменти роботи ідеального імпульсного моменту, тобто у моменти квантування , а у проміжках між моментами квантування система працює як розімкнена при сталому впливі - сигналі, який зберігається на виході формуючої частини імпульсного елементу.

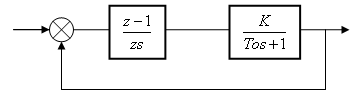
Хай у дискретній системі імпульсний елемент генерує послідовності імпульсів прямокутної форми з періодом та тривалістю , а лінійна частина описується оператором (Рис.84).

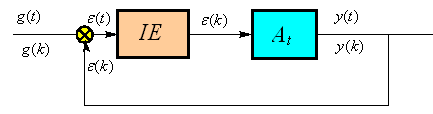
Рис.84 Типова структурна схема дискретної системи.

Вихідний процес , який протікає усередині будь-якого інтервалу дискретності має вигляд

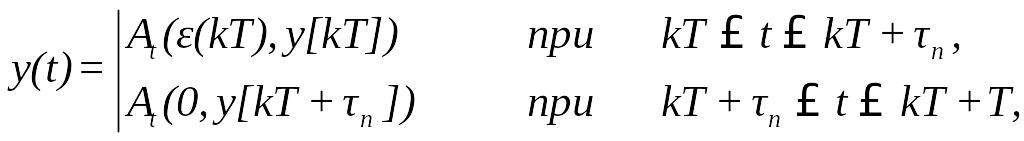(80)

де _..

Кінцеве значення на -тому інтервалі, а отже і початкове значення на інтервалі приймає вигляд

Якщо неперервна частина дискретної системи має -тий порядок, то для визначення рішення необхідно розглядати процес у n попередніх інтервалах дискретності, що зведе рішення до вигляду

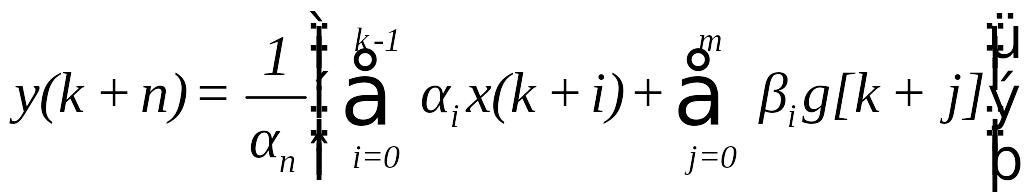(81)

Хай лінійна частина дискретної системи має передаточну функцію , а імпульсний елемент генерує послідовність імпульсів прямокутної форми з періодом та скважністю . Визначимо рішення диференційного рівняння системи у межах одного циклу квантування , який складається із двох рішень на інтервалах та , тобто як рішення рівнянь та .

Рішення на першому інтервалі буде _.

Постійна інтегрування отримується з урахуванням початкових умов для моменту _.

,

Отже, _.

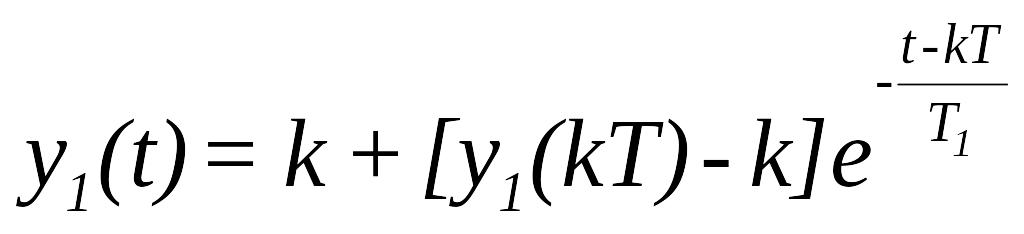На другому інтервалі

Тому що значення на початку інтервалу, тобто при дорівнює значенню на кінці першого інтервалу, то

Отже,

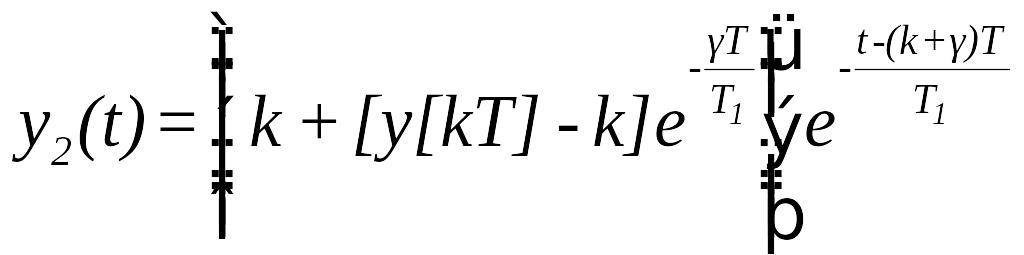
При одержуємо

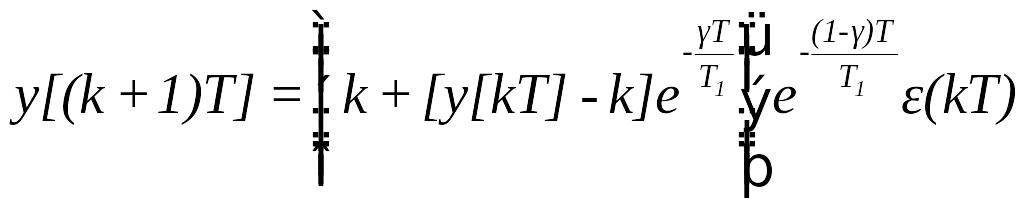
З умови замкнення системи маємо а якщо система замикається одиничним зворотнім зв'язком, то

Отже,

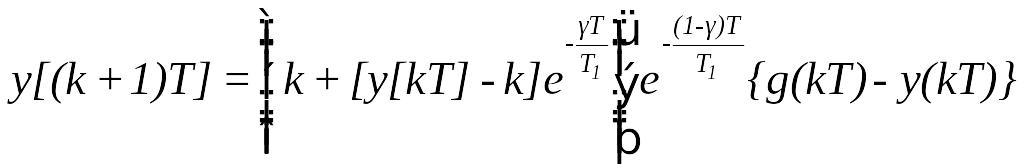
що після перетворень дає

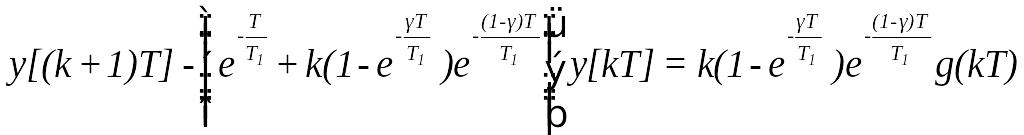
Якщо , то

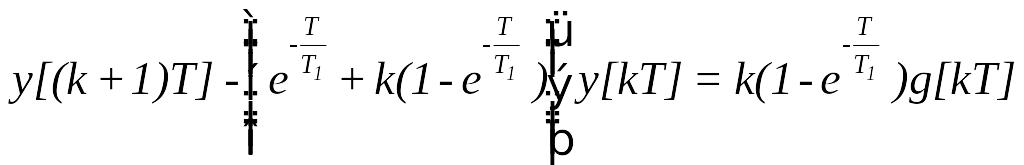
Тому що , то при , ,a _. Із характеристичне рівняння приймає вигляд . Отже,

При ,тобто . Таким чином

Хай , тоді .

Якщо , то процес встановлюється за один крок, система стійка і має найменший час перехідного процесу .

1) При, , що дає коливальний перехідний процес.

2) При процес буде монотонним.

3) При система на межі стійкості.

4) При система стає нестійкою.

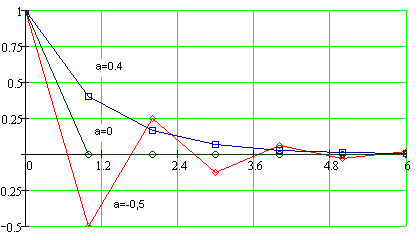
Рис. 85 Вплив кореня на вигляд перехідних процесів

2.3 Вагова (імпульсна) перехідна функція дискретної системи.

Розглянемо так звану зведену вагову функцію розімкненого каналу керування - тобто реакцію неперервної частини системи з екстраполятором нульового порядку на одиничну імпульсну функцію ,або як відношення вихідного сигналу до висоти одиничного імпульсу на вході екстраполятора . Якщо вихідну величину розглядати тільки у дискретні моменти часу , то розімкнений канал керування буде представляти собою імпульсний фільтр .Він може характеризуватися дискретною ваговою функцією , яка здобута із функції .

Дискретна функція дозволяє знайти реакцію імпульсного фільтра на вхідну величину довільного вигляду .

Так реакція імпульсного фільтра на дискретну

y (t) при буде

y (t) при буде

y (t) при буде

Тому , а для дискретних моментів часу

. (82)

Розглянемо дискретну функцію , яка зображує собою імпульсну перехідну функцію , як послідовність значень у дискретні моменти t = 0T,1T,…,nT (Рис.86)

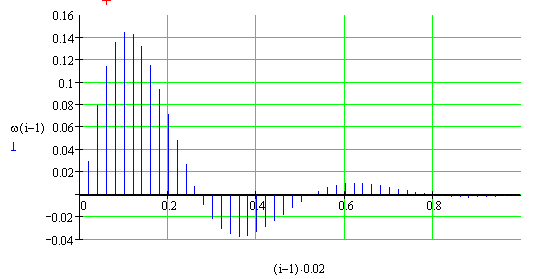
Рис. 86 Вигляд імпульсної перехідної функції

Значення послідовність дискретної функції називаються коефіцієнтами ваги або ваговими коефіцієнтами. Вони характеризують долю питому вагу значень вихідних змінних які діють у різні моменти часу та формують вихідну змінну. Таким чином дискретну вагову функцію можна визначити як

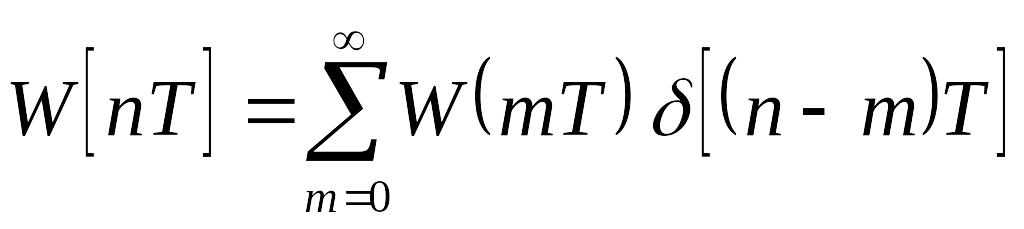₍₈₃₎

Тобто сукупність повністю визначає імпульсну (вагову) функцію дискретної системи.

2.4 Перехідна функція дискретних систем керування

Якщо на вхід дискретної системи з відомою функцією ваги поступає одинична функція , то

(84)

де називається перехідною послідовністю і є аналогом перехідної функції неперервних систем (Рис.87)

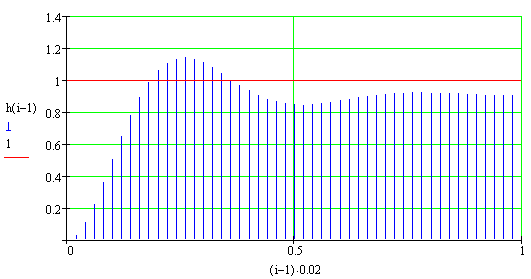
Рис. 87 Вигляд перехідної функції

П 2.24

Побудувати дискретне рівняння для системи керування з фіксатором нульового порядку та оператором лінійної неперервної частини .

1.Визначається рішення диференційного рівняння у межах одного циклу квантування

який складається із двох рішень на інтервалах

та .

1.1 Рішення на першому інтервалі буде

Постійна інтегрування отримується з урахуванням початкових умов для моменту

,

Отже,

1.2. На другому інтервалі , де

Тому що значення на початку інтервалу, тобто при дорівнює значенню на кінці першого інтервалу, то

Отже,

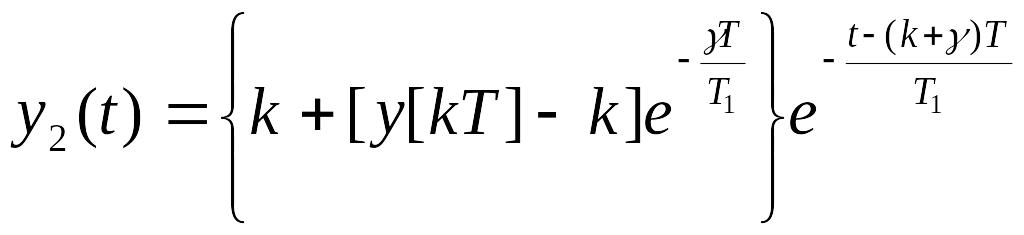
При одержуємо

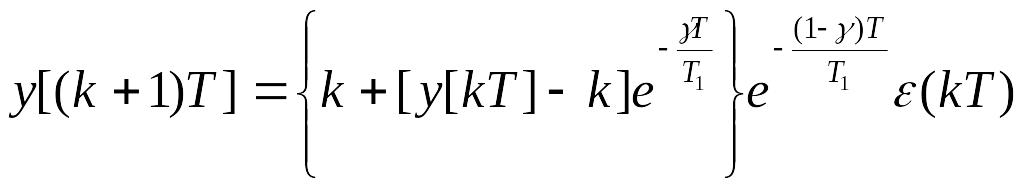
2. Визначається диференційне рівняння для замкнутої системи. З умови замкнення системи маємо а якщо система замикається одиничним зворотнім зв'язком, то

Отже,

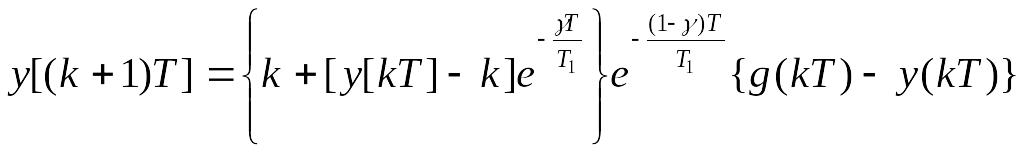
що після перетворень дає

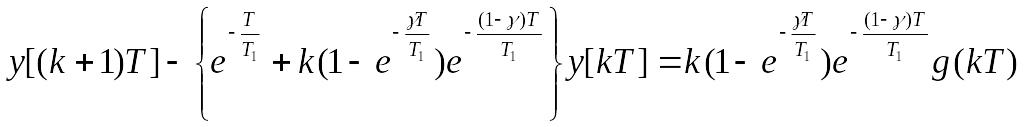
Якщо в системі використовується фіксатор нульового порядку ( ), то

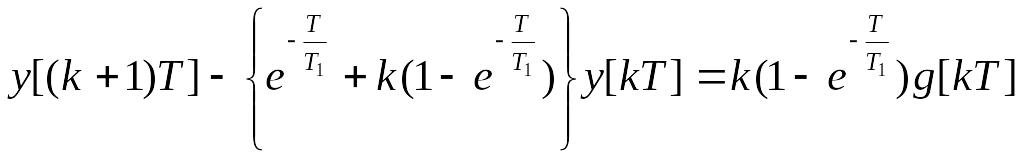
Томущо , то при , , a _.

Із характеристичне рівняння приймає вигляд .

Отже,

При , тобто .

Таким чином

Якщо , то процес встановлюється за один крок.

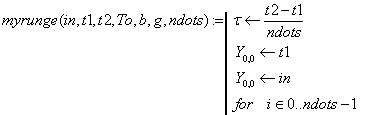
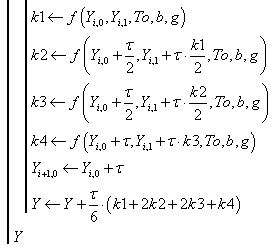
Корень характеристичного рівняння

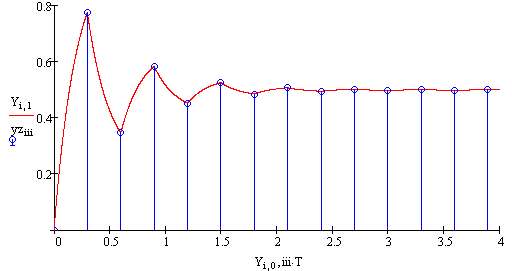
Рис 88 Перехідна характеристика до П

Лабораторна робота №3 Дослідження дискретної системи 1-го порядку

Призначення: Лабораторні дослідження націлені на закріплення знань основних підходів до складання математичної моделі системи керування у вигляді дискретних рівнянь, методів їх розвязання, аналізувати та узагальнювати здобуті експериментальні дані.

Ціль роботи: Виявлення основних співвідношень параметрів системи керування, визначення оптимальних значень параметрів у цілях мінімізації інтегральних оцінок з точки зору кінцевого часу перехідних процесів.

Вибір структури САК та її параметрів виконується виходячи із аналізу функціональної схеми блока моделі узагальненої системи керування віртуального лабораторного стенда та обраних цілей лабораторних досліджень. Значення параметрів системи обирається із таблиці варіантів

В лабораторній роботі необхідно:

1. Скласти математичну модель системи керуванняч у вигляді дискретних рівнянь

2. Розрахувати перехідний процес при заданих значеннях параметрів ЦСАК та визначити співвідношення періоду квантування з коефіцієнтом передачі системи, які забезпечують закінчення перехідного процесй за кінцевий час

3. Побудувати розташування коренів на комплексній площині та оцінити їх вплив на перехідний процес та покажчики якості;

4. Оцінити траєкторії коренів при зміні коефіцієнта підсилення системи;

5. Визначити залежності інтегральних оцінок I=I(K_p), I=I(T₀)

Висновок. Відповідно теоретичним розрахункам та обробки експериментальних досліджень зробити висновки по лабораторній роботі згідно обраних цілей.