2.2 Дискретні рівняння систем керування та методи їх розв’язання.

Хай задана неперервна функція та інтервал квантування T. Тому що змінні, які описують поведінку автоматичних систем, є функціями часу, то у дискретних системах ці змінні розглядаються як послідовність дійсних чисел

_{Числова послідовність, яка є функцією дискретного елементу та яка з'являється у результаті вибірки значень функції x(t) у точках t=kT, називається решітчастою функцією або дискретною функцією x*(t)=x(kT), тобто є послідовністю дискрет (Рис.74).}

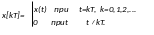( 66)

Кожній неперервній функції відповідає єдина дискретна функція , якщо задано період вибірки .

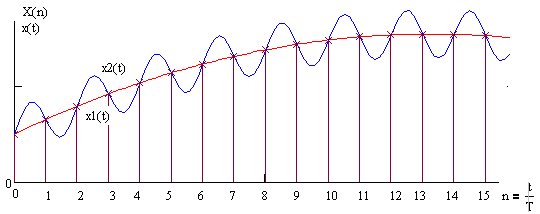
Рис.79 Утворення дискретної послідовності

Однак, за решітчастою функцією неможливо визначити неперервну функцію без додаткових відомостей про її зміну у інтервалах між двома дискретними моментами часу. Так, одна й та сама дискретна функція відповідає двом (гранично безлічі) функціям часу та

Тому з ціллю розширення можливостей використання дискретних функцій вводяться у розгляд зміщені дискретні функції , де - величина зміщення усередині інтервалу дискретності, тобто . Якщо ввести нормований час , то дискретна функція записується як , а її аргументом є елементи цілочислового ряду. При цьому , де визначає параметр зміщення, а сама дискретна функція називається зміщеною дискретною функцією

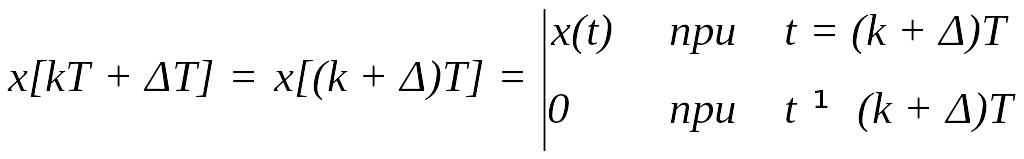
При нормованому часі зміщена дискретна функція записується у вигляді .

Для заданого закону зміни дискретні функції у часі введемо у розгляд поняття різниць та зсувів, які діють під дискретною функцією.

Швидкість зміни дискретної функції ) визначається її першою різницею, яка грає таку ж роль як і перша похідна неперервної функції При цьому може бути визначена перша різниця як різниця між послідуючим та поточним значенням (Рис.80).

, (67)

або зворотна різниця як різниця між поточним та попереднім значенням

. (68)

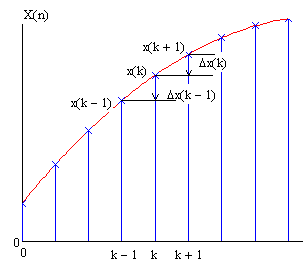
Рис.80 До поняття різниці

Пряма різниця визначається у моменти часу по значенню дискретної функції, яке буде при , зворотна - по значенням, які були у момент часу .

Відповідно, аналогом другої похідної є друга різниця (перша різниця перших різниць)

.

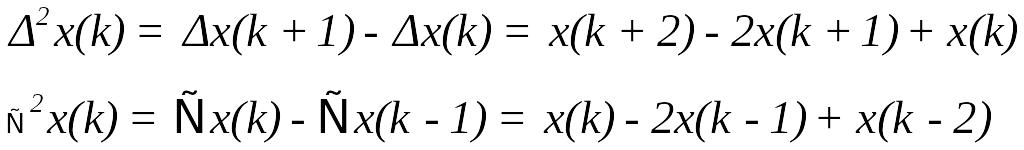Для обчислення n-ої різниці використовуються співвідношення

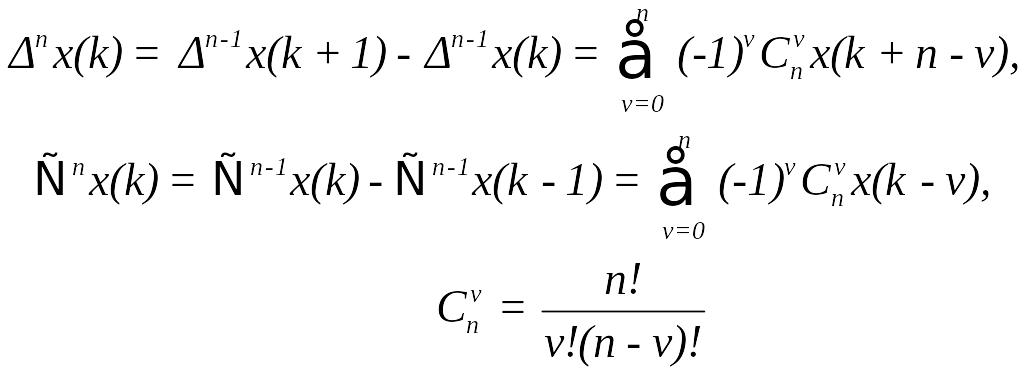(69)

Розглянемо питання відновлення неперервного сигналу із послідовності імпульсів з амплітудою у момент часу . Цей процес можна розглядати як процес екстраполяції, тому що неперервний сигнал повинен бути відтворений на підставі інформації, яка була доступна тільки у попередні моменти часу.

Для цього розкладемо неперервну функцію у ряд на інтервалі між двома моментами вибірки та , тобто

₍₇₀₎

де при ,

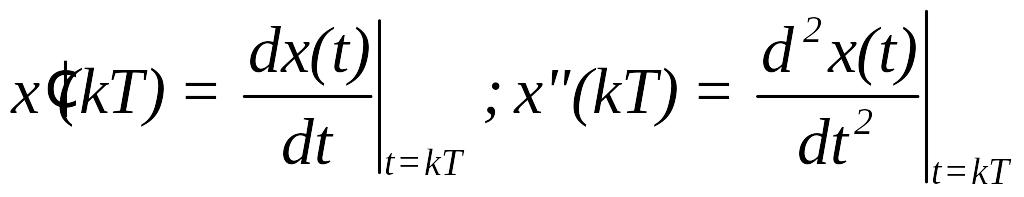
Для того, щоб обчислити коефіцієнти ряду, похідні функції повинні бути одержані у моменти вибірки, тобто похідні повинні обчислюватися по значенням Простий вираз, який включає тільки два дискретних значення дає оцінку першої похідної у моменти у вигляді

(71)

Апроксимоване значення другої похідної дає

(72)

Таким чином, чим вище похідна, тим більше число потрібних попередніх вибірок.

Так для апроксимації треба вибірка.

Отже, описаний вище екстраполюючий пристрій складається із набору часових затримок на період , число яких залежить від точності оцінки функції часу

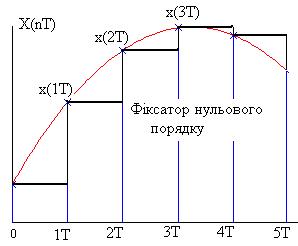
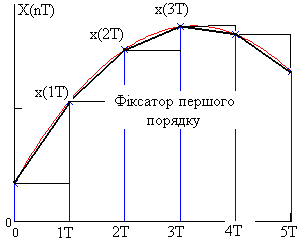
Рис .81 До поняття дії фіксаторів нульового та першого порядків

Пристрій, у якому реалізовано тільки член для інтервалу часу , називається екстраполятором нульового порядку, бо поліном, який використовується для цього, має нульовий порядок. Подібний пристрій також широко відомий як фіксатор нульового порядку, оскільки він фіксує значення попередньої вибірки протягом одного періоду квантування до послідуючої вибірки. Пристрій, який реалізує перші два члени розкладу, називається фіксатором першого порядку ( Рис.81).

Запроваджуємо поняття оператору зсуву, який визначається такою залежністю:

прямий зсув

зворотній зсув (73)

При цьому, у силу того що

оператор різниці можна зобразити через оператор зсуву та навпаки

(74)

Відповідно,

,

. (75)

Отже, аналогічно диференційним рівнянням можна побудувати деякий оператор , який буде зображений через відповідні різниці і який деякій вхідній послідовності буде ставити відповідну вихідну послідовність , тобто

називається різницевим рівнянням (дискретним рівнянням),яке зв'язує між собою шукану дискретну функцію з її різницями із різницями дискретної функції

Якщо оператор є лінійним, то і відповідне дискретне рівняння є лінійним.

Якщо у дискретне рівняння аргумент не входить явно, то відповідне рівняння є стаціонарним.

При можливості розподілу змінних лінійне рівняння зводиться до вигляду

, (76)

де оператори та є операторами відносно операції здобуття різниць, тобто

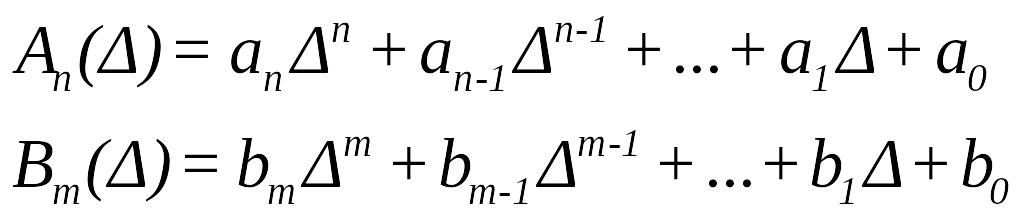
Дискретне рівняння може бути записано і через оператор зсуву, якщо виразити

₍₇₆₎

але при цьому коефіцієнт поліномів та не будуть еквівалентні.

Дійсно, хай дискретне рівняння має вигляд

Якщо використати підстановку ,то

,

і після групування коефіцієнтів при однакових степенях одержимо

, (77)

де

Так, при

використовуючи заміну ,здобудемо

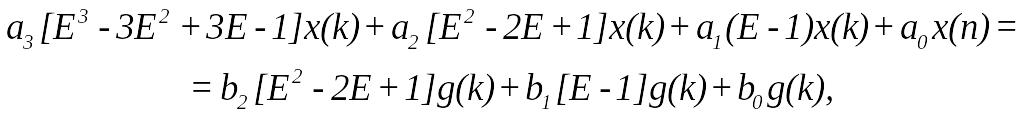
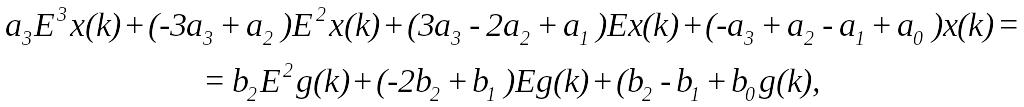
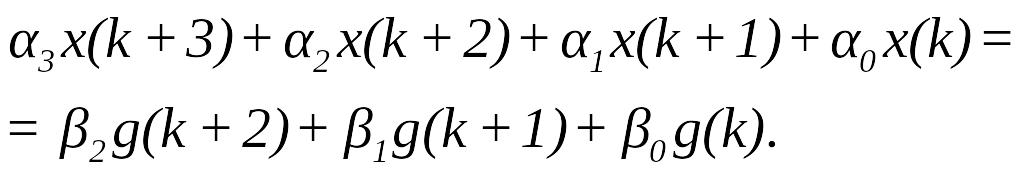
Використовуючи рівняння відносно оператору зсуву можна здобути рішення через рекурентне співвідношення

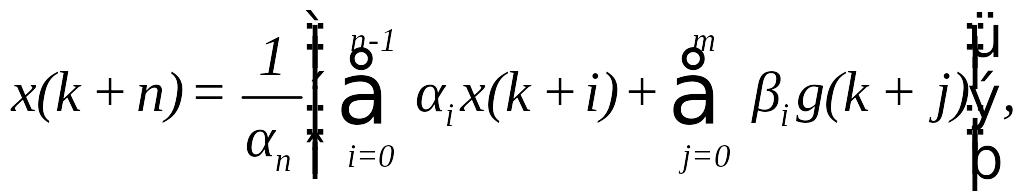(78)

яке дозволяє визначити послідовність ,..., якщо визначені початкові умови та значенням дискретної функції Алгоритм рішення легко реалізується на ЕОМ.

Хай задано дискретне рівняння та визначені i .

Отже,

_{Зображення дискретної послідовністі представлено на рис.82}

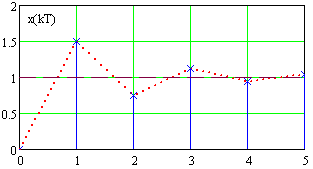
Рис .82 Дискретна послідовність

У загальному випадку рішення дискретного рівняння складається з вільного та вимушеного руху

,

де визначає вільний рух, як рішення однорідного рівняння

а визначає вимушений рух, як окреме рішення, яке залежить від виду вхідного сигналу.

Вільне рішення здобувається у вигляді

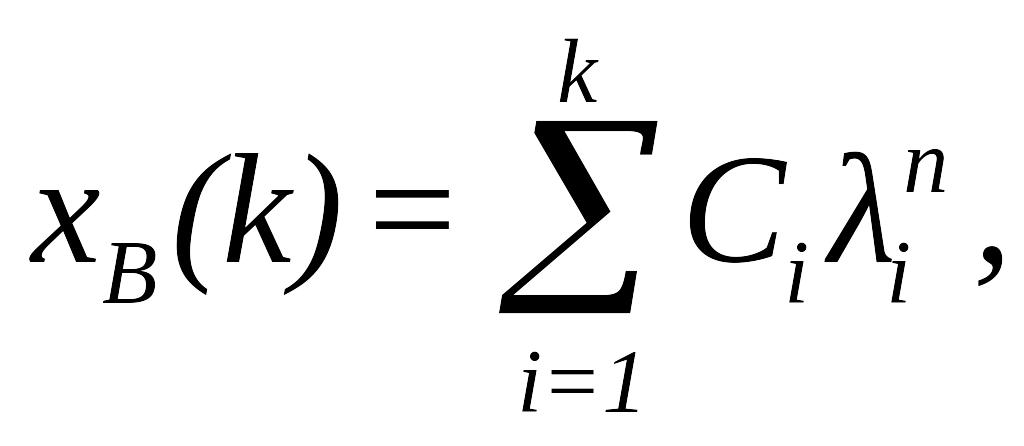(79)

де - корені характеристичного рівняння

Аналіз вільного руху показує, що для стійкого руху необхідно і достатньо, щоб використовувались умови , (32), тобто, властиві значення характеристичного поліному стійкого руху повинні належати колу одиничного радіусу (Рис.83).

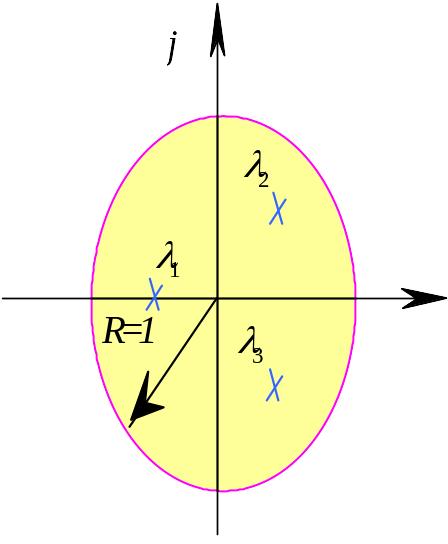
Рис .87 Розташування коренів у колі одиничного радіусу

Очевидно, що коли дійсні, то представляє собою монотонний процес, коли - комплексні, то процес буде коливальним, якщо , то процес буде встановлюватись за один крок.