1.11 Дискретні сигнали.

В останнiй час знайшли розповсюдження системи з цифровою обробкою сигналiв при якої аналоговий сигнал перетворюється у цифрову форму, пiсля чого виконується його обробка i далі вiдбувається перетворення у аналоговий вихiдний сигнал. Тому треба знати, за яких умовах iз часової послiдовностi можливо таке зворотне перетворення.

Хай - аналоговий сигнал. Йому вiдповiдає дискретна вибірка, тобто часова послiдовнiсть , де – тактовий перiод, – номер вiдлiку.

Якi умови тотожності цих сигналiв? Аналоговий сигнал може бути поданий у частотнiй областi за допомогою пари перетворень Фур’є:

Спектральна функція послiдовностi визначається дискретним перетворенням Фур’є:

₍₆₂₎

При розв’язанні практичних задач може використовуватися кінцеве число вiдлiкiв аналогового сигналу.

₍₆₃₎

Який же зв'язок мiж зображенням та зображенням Фур’є дискретної функцiї ? Зобразимо процес квантування сигналу амплітудною модуляцiєю послiдовностi -функцiй аналоговим сигналам (Рис.74).

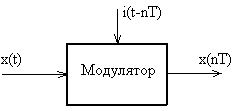
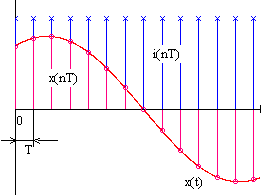
Рис.74 Процес квантування сигналу амплітудною модуляцiєю

послiдовностi -функцiй аналоговим сигналам

Послiдовнiсть є послiдовнiстю -функцiй передаточної функцiї iз перiодом , тобто вона є періодичною функцією і тому може бути розкладена у ряд Фур’є:

Знайдемо зображення -го члена послiдовностi, використавши спiввiдношення

тобто

₍₆₄₎

Для

Таким чином спектр нульового такту сигналу пропорцiйний спектру аналогового сигналу, спектр імпульсу першого такту пропорцiйний спектру нульового такту, але змiщений на величину , яка дорiвнює частотi квантування сигналу. Спектр всiєї послідовності можна визначити як суму спектрiв кожного iмпульсу всiєї послiдовностi, тобто

(65)

пропорцiйний сумi змiщених спектрiв неперервної модулюючої функцiї.

Якi умови вiдновлювання неперервного сигналу iз його дискретної послiдовностi?

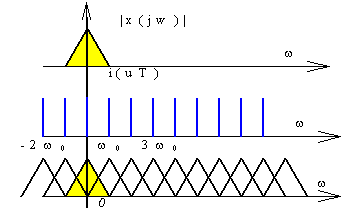
Рис.75 Співвідношення спектрів неперервного сигналу та його дискретної послідовності

Хай аналоговий сигнал має частотний спектр з максимальною частотою спектра (Рис.76).

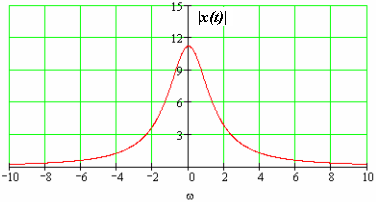
Рис. 76 Амплітудно-частотної спектр неперервного сигналу

Сигнали квантуються з перiодом , тобто iз частотою . Знайдемо дискретний спектр цiєї послiдовностi. Якщо цей спектр пропустити через фiльтр iз рівномірною полосою пропускання у межах то на виходi фiльтру з'явиться частотний спектр, який може не відповідати частотному спектру досліджуваного аналогового сигналу.

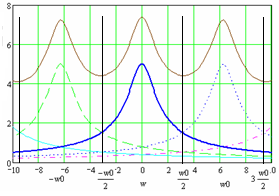
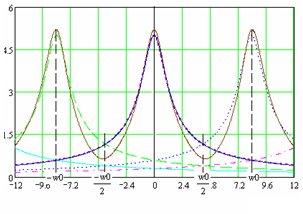
Рис. 77 До питання відновлення неперервного сигналу з його дискретної послідовності

Якщо пiдвищити частоту квантування сигналу таким чином, щоб змiщенi частотнi спектри не перекривалися, тобто , то на виходi фiльтру з'явиться спектр, який буде дорiвнювати частотному спектру досліджуваного сигналу, тобто неперервний сигнал може бути вiдновлений iз його дискретної послідовності (Рис.78 ).

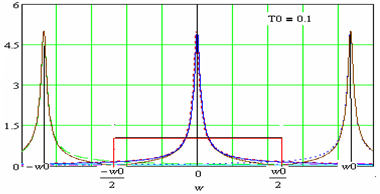
Рис. 78 Відновлення неперервного сигналу з його дискретної послідовності

Висновок: Для того, щоб дискретну систему можна було розглядати як неперервну, треба щоб виконувалася умова теореми Котельникова-Шеннона, тобто частота квантування сигналу повинна бути не менш як в два рази бiльше максимальної частоти спектру, який є в цьому сигналi

Лабораторна робота №2 Дослідження дискретних сигналів.

Призначення: Лабораторні дослідження націлені на закріплення знань основних принципів представлення сигналів, які діють в цифрових системах автоматизованого керування технологічними процесами, надання навичок застосування сучасних методів математичного опису дискретних детермінованих сигналів керування, здобуття умінь ставити та розв’язувати задачі, зв’язані описом систем керування, аналізувати та узагальнювати здобуті експериментальні данні.

Ціль роботи: Знайомство з типовими детермінованими сигналами ,що описують задаючи та збуджуючи впливи, з їх часовими та частотними характеристиками , методами їх обробки.

Вибір структури САК виконується виходячи із аналізу функціональної схеми блока обраних цілей лабораторних досліджень. Значення параметрів сигналів обирається моделі узагальненої системи керування віртуального лабораторного стенду та довільно

У лабораторній роботі необхідно:

1. Дослідити типові детерміновані сигнали, визначити їх дискретні послідовності та частотні характеристики.

2. Експеріментально доказати умови відновлювання сигналу з його дискретної послідовності

Висновок. Відповідно теоретичним розрахункам та обробки експериментальних досліджень зробити висновки по лабораторній роботі згідно обраних цілей досліджень.

Розділ ІІ Математичні моделі систем керування

2.1 Системний підхід до складання математичних моделі систем керування.

Складнiсть систем автоматичного керування визначається призначенням, задачами, властивостями об'єктiв керування, тобто об'ємом перероблюваної iнформацiї. Ступiнь складностi об'єкта керування зв'язана з числом контурiв, наявнiстю внутрiшнiх перехресних прямих та зворотних зв'язків, порядком диференцiйних рівнянь, розміром матриць, за допомогою яких описується динаміка системи. Знання особливостей математичних моделей, методiв та алгоритмiв рiшення технічних питань необхiдно iнженеру для успiшної постанови задач, для слушного формулювання початкових даних та iнтерпретацiї здобутих результатiв, при прийнятті рiшень про використання тих чи iнших компонентiв математичного забезпечення у процесi розробки проектних задач. Перед розробкою моделi фiзичного процесу необхiдно чiтко сформулювати цiлi та задачі керування, тому що моделi одного i того ж фiзичного процесу можуть мати мало загального, якщо вони розроблювались для рiзних цілей. Тому перед розробкою математичної моделi процесу необхiдно вирiшувати наступнi задачі: 1.Область дiї та межi вивчаємого процесу. 2. Глибина деталiзацiї фiзичного явища. 3. Фiзичнi обмеження та обмеження, які визначаються умовами безпечностi.

4. Характер керування у сталих та динамічних режимах роботи. 5. Необхiднiсть удосконалення моделi. 6. Змiннi стану та вiдомi змiннi керування. 7. Збуджуючі впливи, якi дiють на систему та некерованi змiннi. Базою для розробки моделей процесу та опису дiючих сигналiв є основнi закони фiзики та хiмiї, дiючих у пневматичних, гiдравлiчних, теплових, механiчних та електричних системах. При трактуваннi основних законiв треба виходити iз єдиного системного пiдходу, що дозволяє iнженеру переходити вiд однiєї областi знань до iншої, наприклад, вiд гiдравлiки до електротехнiки, вiд теплотехнiки до механiки i т.п.

Запам'ятайте! Надто докладний математичний опис, який ураховує неособливi для даної задачi властивостi елементiв, ускладнює рiшення задачi та може зробити її нерозв'язуємою.

Але надмірне спрощення задачi, прийняття необгрунтованих припущень недопустимо, тому що при цьому можуть бути упущенi iстотнi властивості процесiв у системi!

На кожному iєрархiчному рiвнi опису системи можуть використовуватися свої математичнi моделi, складнiсть яких погоджена з методом здобуття моделi та iз можливостями аналiзу! У теорiї автоматичного керування є достатньо розробленi iнженернi методи, якi дозволяють розв'язувати складнi задачі аналiзу та опису систем.

Аналiз систем позначає, що система керування вже побудована або визначено її математичний опис i потребується вивчити її характеристики та показники якості роботи у заданих умовах.

Термiн "синтез" вiдноситься до ситуацiї, коли задаються бажані вимоги до системи (показники якості), а необхідно знайти математичне рiшення задачі та визначена процедура цього рiшення, тобто необхiдно побудувати систему, яка задовольняє поставленим вимогам.

На першому етапi аналiзу виконується аналiз властивостей системи, вививчається структура цiєї системи, викриваються схеми відносин між елементами її структури. Пiсля виявлення всiх елементiв системи та встановлення структури їх зв'язкiв та вiдношень викривається суть кожного елементу, структурні вiдношення у серединi самих елементiв.

Існують декiлька пiдходiв до рiшення поставлених задач.

Перший пiдхiд базується на операторних методах, які мають справу iз перетвореннями у площинi комплексних змiнних S або Z, а також на методi кореневого годографу. При проектуваннi систем керування звичайно треба задовольнити ряду вимог, якi пред'являють до часових або частотних характеристик, до структури системи. Тому на цьому етапi аналiзу виконується оцiнка стiйкостi системи, здiйснюється вибiр структури та параметрiв, якi забезпечують стiйкiсть системи, оцiнюються запаси по пiдсиленню, по фазi, по показнику коливань та часу перехiдних процесів. Потім оцiнюється точнiсть системи при вiдпрацюваннi типових впливiв. Щоб задовольнити заданi вимоги виконується корекція параметрiв, корекцiя частотних та часових характеристик системи.

Другий пiдхiд, який часто-густо зветься аналiтичним, заснований на використанні оцінки якостi системи (iнтегральних квадратичних або середньоквадратичних похибок). При цьому проектування зводиться до розрахунку компенсуючих фiльтрiв.

Третiй пiдхiд до проектування систем полягає у визначеннi закону або стратегiї оптимального керування, при якому мiнiмiзується або максимiзується деяка сукупнiсть критерiїв якості. При цьому синтезуються закони керування, якi визначають керуючі впливи у виглядi функцiй координат стану об'єкта, що у результатi приводить до систем iз зворотними зв'язками.

Треба враховувати, що реальнi системи керування у більшості випадків є нелiнiйними. Тому для аналiзу та синтезу систем автоматичного керування бажано перейти до лiнеаризованих методiв, які використовують добре розробленi iнженернi методи проектування та розрахунку лiнiйних систем. У випадках, коли неможливо здiйснити операцiї лiнеаризацiї, тобто коли система буде суттєво нелiнiйною, методи, які пристосовані для розрахунку лiнiйних систем, стають недоцiльними. В цих випадках використовуються частинні методи аналiзу нелiнiйних систем , тому що в наш час загальних пiдходiв до їх розрахунку немає. При цьому кожний конкретний випадок потребує своїх методів для оцінки властивостей нелiнiйних систем та вибору необхiдних параметрiв.