1.10.9 Основнi властивостi -перетворення

1. Властивiсть лiнiйностi – зображення лiнiйної комбiнацiї дискретних функцiй дорiвнює тій самій лiнiйній комбiнацiї їх зображень.

Хай

Тодi ₍₄₇₎

2. Теорема зсуву.

Розглянемо функцiю запізнення , тобто яка має зсув на цiле число тактiв .

Якщо покласти то

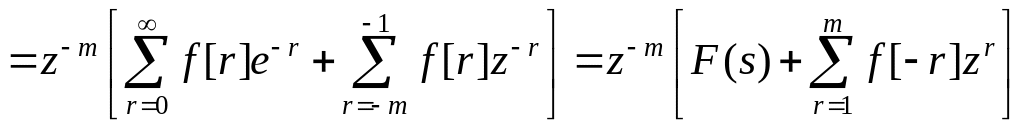₍₄₈₎

Якщо вихідна функцiя при вiд'ємних значеннях аргументу дорiвнює нулю, то

Якщо зсув виконується праворуч (упередження), то

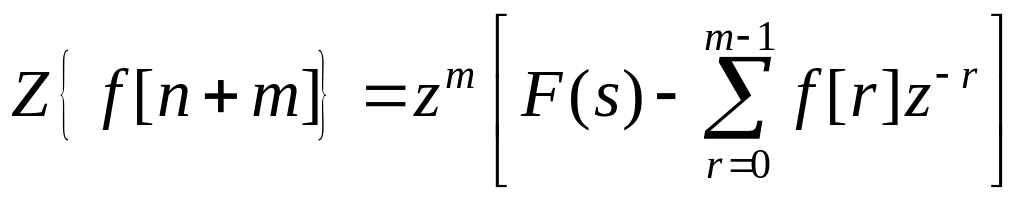₍₄₉₎

3. Зображення рiзниць.

Вiдповiдно теорiї зсуву

.

При нульових початкових умовах ₍₅₀₎

Аналогiчно, ₍₅₁₎

Зазначимо, що при (неперервнi системи)

,

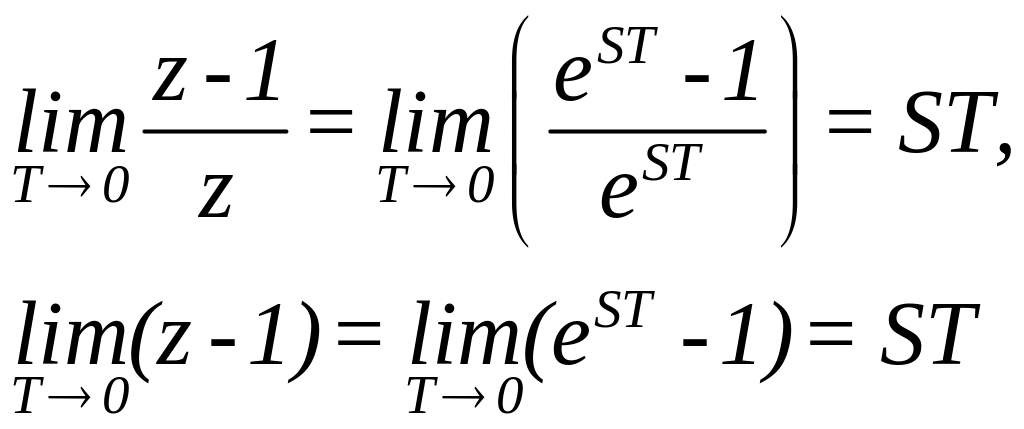що iлюструє схожiсть зображень похiдних та рiзницi.

4. Кiнцеве значення дискретної функцiї.

Визначимо зображення першої прямої рiзницi функцiї

Знайдемо суму ординат

(52)

Тому що ,

а при , , то

Таким чином (53)

Порiвнюючи вирази (52) та (53) для здобудемо

₍₅₄₎

5. Зв'язок дискретних рівнянь з їх -зображеннями.

Хай дискретне рiвняння має вигляд

₍₅₅₎

Згiдно теореми зсуву запишемо

Тодi

(56)

Вивчення вiдносин мiж та - площинами при перетвореннi є важливим у зв'язку з можливостями аналiзу розташування нулiв та полюсiв передаточної функцiї системи на вiдповiдних площинах.

Розглянемо основну смугу та видiлимо у неї контур 1-2-3-4-5-1.

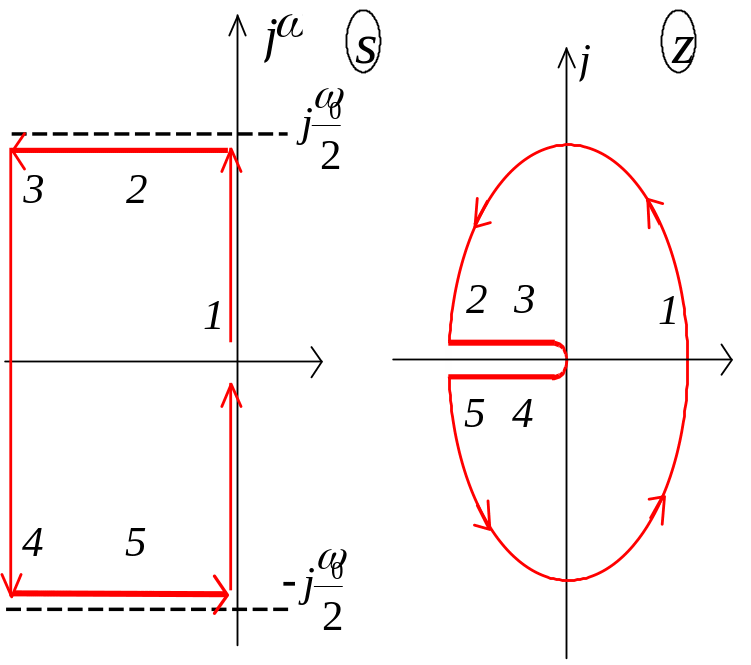
Рис. 67 Співвідношення основної смугг до одиничного кола

Тому що

, (57)

то всi додатковi смуги півплощині -площини вiдображаються у теж саме одиничне коло на -площинi, а всi точки, якi належать вiдповiдному контуру, якi вiдображуються усередину одиничного кола.

Лiнiї на - площинi, якi паралельнi уявної осi, тобто лiнiї сталого загасання для неперервних систем, вiдображаються на -площинi колом радiусу ( Рис. 68)

Рис.68 Співвідношення лінії сталого згасання

Для будь-якої лiнiї на -площинi на -площинi буде вiдповiдати лiнiя, яка виходить iз початку координат пiд кутом рад.

П 1.13

Визначити інтервал дискретності , при якому ступінчатий опис функції по дискретним точкам не приведе до похибки не більше ніж 5% початкового значення.

• Найбільша крутизна заданої функції спостерігається у точці

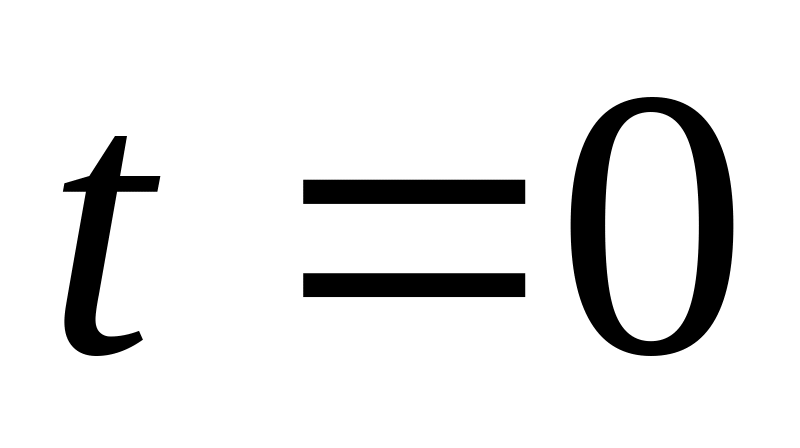
Початкове значення . На першому інтервалі .

Відкіля

П. 1.14

Для експоненціальної функції визначити інтервал дискретності , при якому лінійна інтерполяція значень функції у середині проміжків між дискретними точками не перевищує 1% початкового значення.

• На першому інтервалі 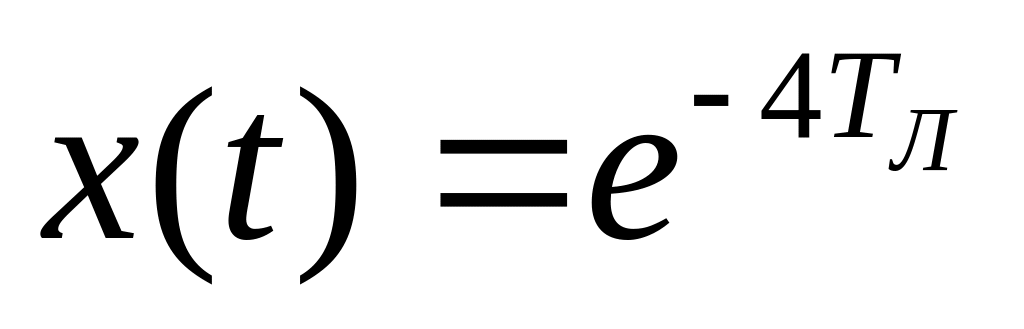для середини відрізку 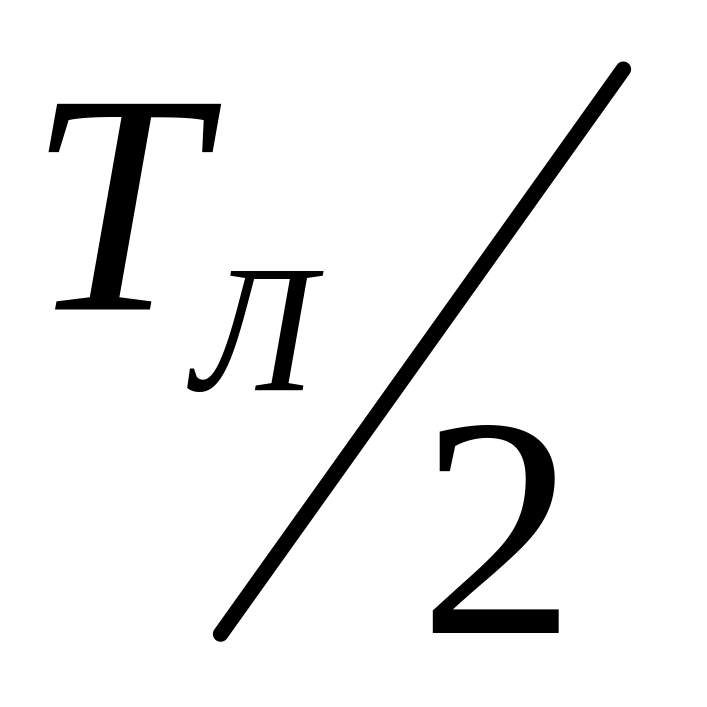дає , тоді як фактичне значення для буд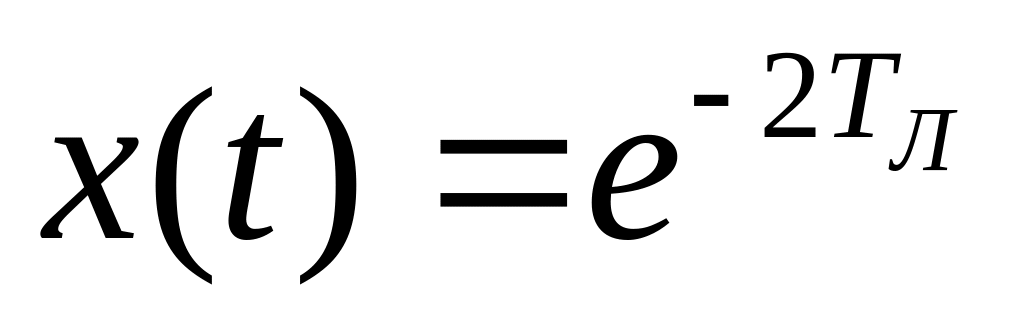е . Отже,

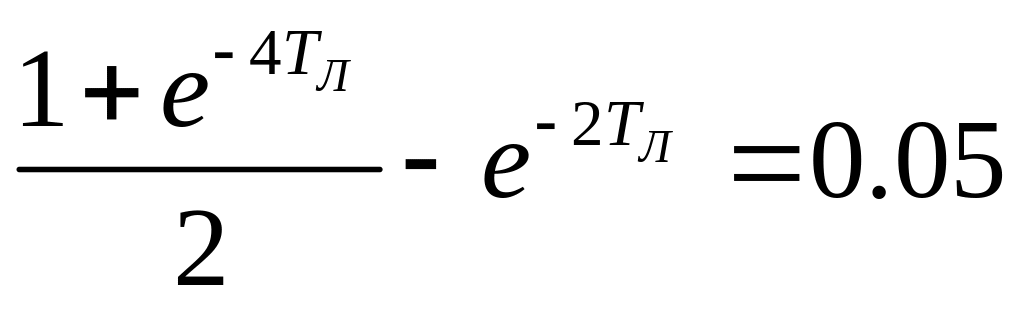
П 1.15

Для експоненціальної функції визначити - перетворення

Тому що , а перетворення Лапласа

, то з урахуванням . Отже,

.

Для та .

П 1.16

Для при знайти зворотне - перетворення

Для цього треба розкласти по від’ємним степеням

.

П 1.17

Приклад переходу від перетворення Лапласа до перетворення

Задано оператор з фіксатором нульового порядку на вході

1. Визначається зворотне перетворення

2. Визначається перетворення

3. Додається співмножник та спрощується вираз для

3. Спрощується результат

або

3. Визначається перехідний процес

3. Порівняння перехідних процесів дискретного та неперервного

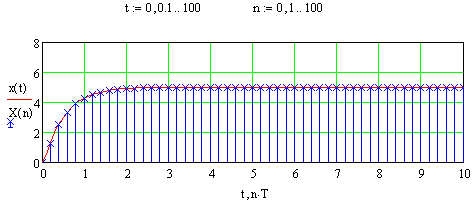
Рис.69 Перехідні процеси до П.

П 1.18

Приклад переходу від перетворення до дискретного перетворення Лапласа та побудови амплітудо-частотної характеристики

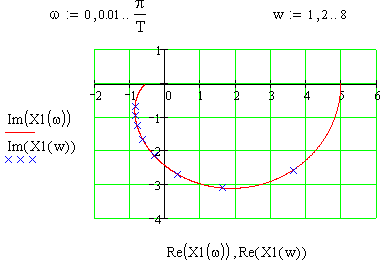
Рис.70 Амплітудо-фазо-частотної характеристика до П.