1.10.4 Властивості перетворення Фур’є

1. Якщо функції перетворюються по Фур’є та їх спектральні характеристики є відповідно і якщо - величини які не залежать від та ,то

Дійсно

2. Якщо функція та її похідна перетворюються по Фур’є та має спектральну характеристику , то спектральна характеристика похідної

Дійсно,

При однобічному перетворенні , де

3. Якщо функція перетворюється по Фур’є та має спектральну характеристику , то спектральна характеристика інтеграла

4. Якщо функція перетворюється по Фур’є та має спектральну характеристику , то спектральна характеристика зміщеної функції , де – додатне число,

Для

5. Якщо функція перетворюється по Фур’є i - її спектральна характеристика, то

6. Якщо функція перетворюється по Фур’є i - її спектральна характеристика та - додатне дійсне число, то

7. Теорема Парсеваля. Якщо функції та перетворюються по Фур’є i , - їх спектральні характеристики, то

Якщо покласти , то та

де - енергетична спектральна характеристика неперіодичної функції .

8. Згорток двох функцій та

Якщо функції та перетворюються по Фур’є i , - їх спектральні характеристики, то спектральна характеристика згортки

Дійсно

П 1.9

Приклад побудови амплітудно-фазо-частотної та спектральної характеристики неперервної ланки

1. Перехід до частотних характеристик

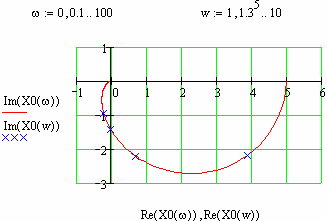
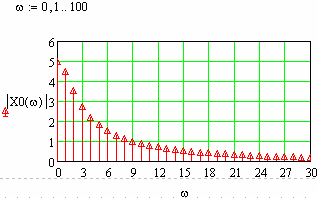
Рис.57 Частотні характеристики неперервної ланки

1.10.5 Дискретне перетворення Лапласа.

Хай маємо імпульсивний сигнал (31)

Зображення по Лапласу

(32)

Якщо записати та записати , то .

Якщо у зробити заміну , то

Перетворення Лапласа є однозначним, тобто якщо є , то є його оригіналом. Для – перетворення зворотне перетворення не є однозначним, бо відповідає тільки у дискретні моменти квантування , а між моментами квантування є не визначеними та може приймати будь яке значення. Ця неоднозначність зворотного – перетворення є обмеженням, про яке слід пам’ятати при застосуванні апарату – перетворення. Зворотне – перетворення позначається як . Методи визначення : 1. Метод розкладу на прості дробі. У неперервних системах зворотне перетворення Лапласа може бути здобуто розкладом у вигляді простих дробів При цьому Для дискретних систем для функції існує відображення Отже, для розкладу слід приймати не , а із подальшим помноженням на . Тоді

П 1.10

1. Знаходження оригіналу дискретного сигналу по його Z-зображенню

По таблицям знаходимо

Отже,

2. Метод розкладу у степеневий ряд. Із формули – перетворення витікає

,

де коефіцієнти ряду є значеннями у моменти . Якщо перший метод дає запис у компактній формі, то другий є послідовністю чисел.

П 1.11

1. Знаходження оригіналу дискретного сигналу шляхом розкладу у ряд по степеням

Отже,

Розглянемо сигнал, який утворений послідовністю одиничних імпульсів, які діють у моменти та модульовані функцією

₍₃₃₎

Права частина цього рівняння складається із величин, які визначаються значеннями сигналу у дискретні моменти часу . Якщо значення фіксоване, то ці величини можна розглядати як функції дискретного часу. Такі функції звуться решітчастими або дискретними.

Так одинична решітчаста (дискретна) функція має вигляд ( рис. 58)

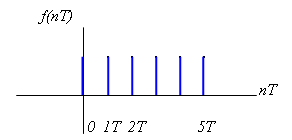
Рис.58 Одинична решітчаста (дискретна) функція

Таким чином

Якщо розглядати послідовність імпульсів, що діють у моменти , то

При цьому дискретний сигнал можна записати у безрозмірному часі

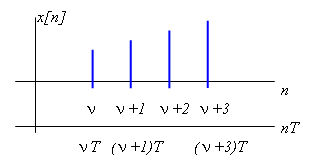
Рис.59 Відносна дискретна послідовність

Зміщений дискретний сигнал записується у вигляді

Такий сигнал позначається як

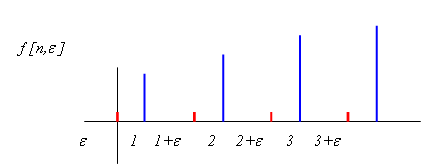
Рис.60 Зміщена дискретна послідовність

В останнiй час знайшли розповсюдження системи з цифровою обробкою сигналiв, при якої аналоговий сигнал перетворюється у цифрову форму, пiсля чого проходить його обробка i потім вiдбувається перетворення у аналоговий вихiдний сигнал. Тому треба знати, за яких умовах iз часової послiдовністi можливо таке зворотне перетворення.

Хай -аналоговий сигнал. Йому вiдповiдає дискретна часова послiдовнiсть , де – тактовий перiод, – номер вiдлiку.

Якi умови тотожності цих сигналiв? Аналоговий сигнал може бути поданий у частотної областi за допомогою пари перетворень Фур’є:

Спектральна функція послiдовністi визначається дискретним перетворенням Фур’є:

₍₃₄₎

При розв’язку практичних задач може використовуватися кінцеве число вiдлiкiв аналогового сигналу.

₍₃₅₎

Розглянемо процес перетворення неперервного сигналу ідеальним імпульсним елементом, що представляє собою амплітудну модуляцію послідовності дельта-імпульсів неперервним сигналом (Рис.61).

Рис. 61 Ідеальний імпульсний елемент з амплітудною модуляцією

В цьому випадку , але є послідовністю миттєвих імпульсів одиничної площини. Отже, площини вихідних імпульсів дорівнюють значенням вхідної функції у дискретні моменти часу.

Тоді .

Знайдемо зображення k-го імпульсу вихідної послідовності

Тому що для -го моменту , то можна записати

Отже, зображення Лапласу всієї послідовності дає

₍₃₆₎

Цей вираз i визначає дискретне перетворення Лапласу