1.10.2 Властивості перетворення Лапласа.

Лінійність зображень. Якщо ,

то

Зображення похідної. Якщо то

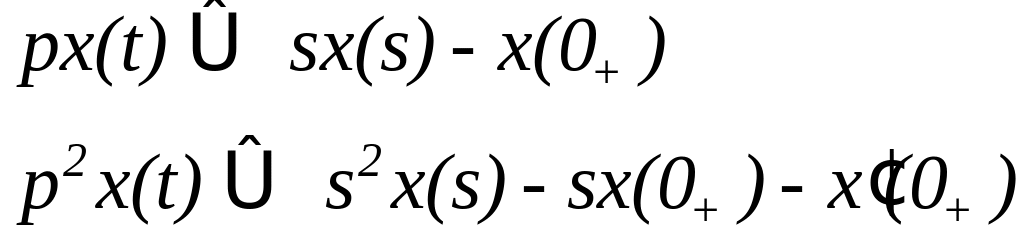
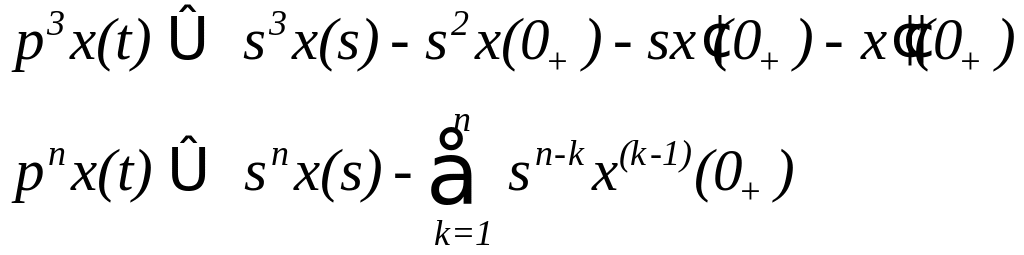
Теорема зміщення. Якщо

Теорема затримки. Якщо

Теорема про диференціювання описуючої функції. Якщо , то

Теорема добутку. Якщо

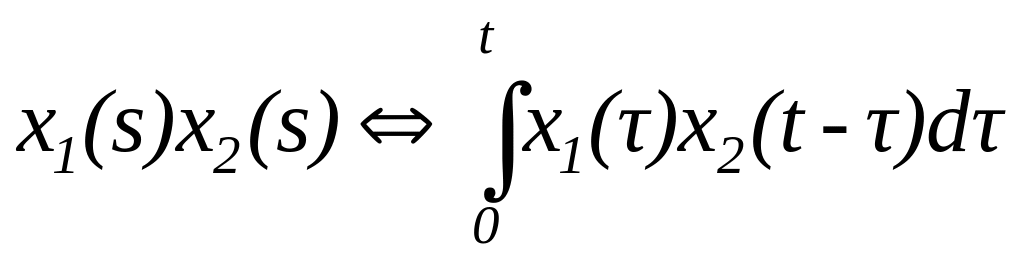
Поведінка оригінала у нулі. Якщо та

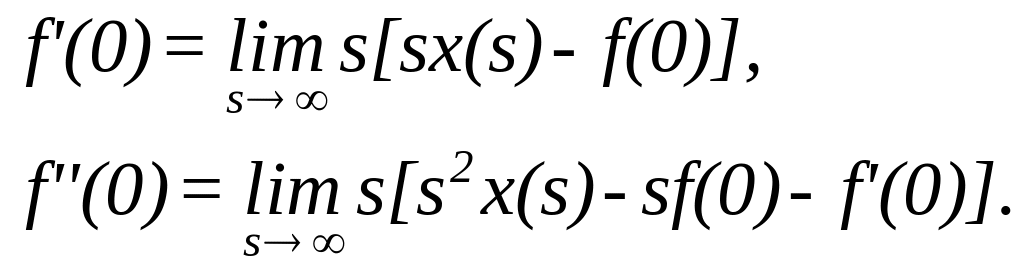
оведінка оригінала на нескінченності. Хай - правильна раціональна дріб. Якщо усі полюси розташовані лівіше від мінливої осі, то

Операцію знаходження оригінала по зображенню називають перетворюванням зображення. На практиці ця операція виконується за допомогою таблиць. Але виликий інтерес має загальна формула

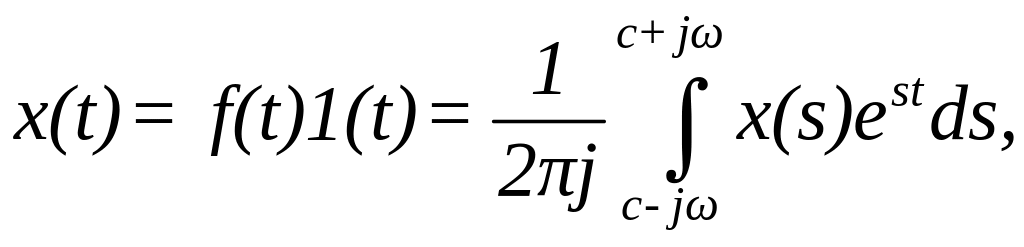
у якої границі інтегрування позначають, що точка пробігає на комплексної площині пряму, яка паралельна мінливої осі. Цей інтеграл за прямою треба розуміти як границю інтеграла по симетричному шляху від до при , тобто

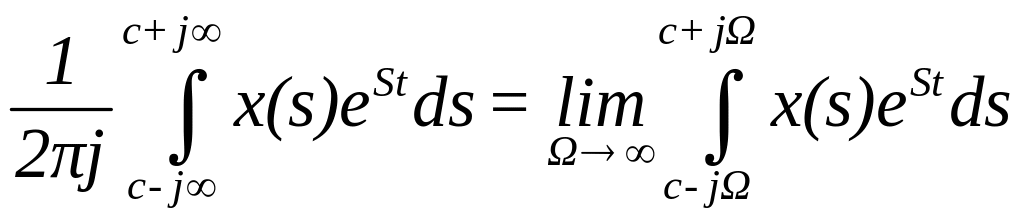
Для збігання зворотного інтеграла необхідно щоб пряма, вздовж якої проводиться інтегрування, розташовувалась правіше усіх особливих точок функції , тобто, якщо - дійсна частина самої особливої точки, то треба щоб .

П 1

1. Знаходження зображення сигналу ( пряме перетворення Лапласа )

,

, ,

,

2. Знаходження оригіналу ( зворотне перетворення Лапласа )

1.10.3 Перетворення Фур’є .

Зображення по Лапласу є функція, яка задана на усієї площині комплексного аргументу , за виключенням деяких особливих точок. Якщо покласти , тобто . То зображення по Лапласу переходить у зображення по Фур’є сигналу .

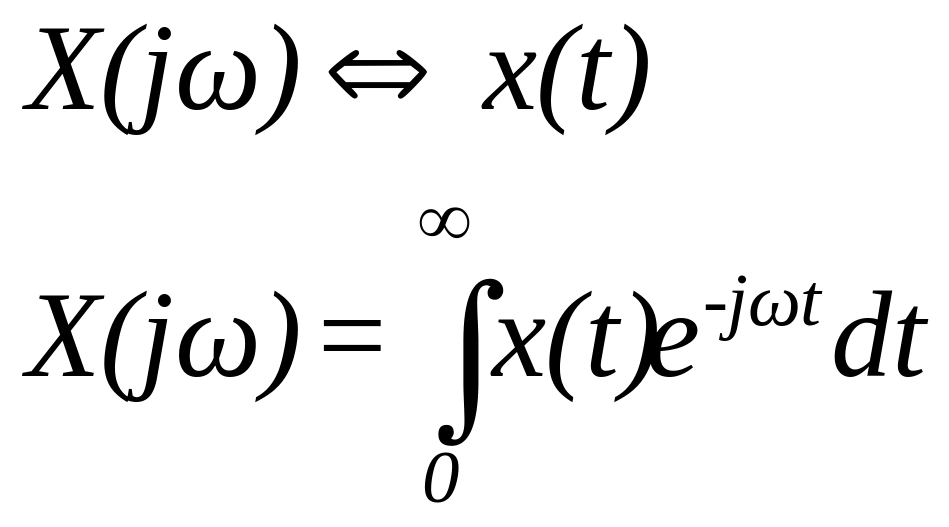(27)

Якщо представити , то

Відповідно

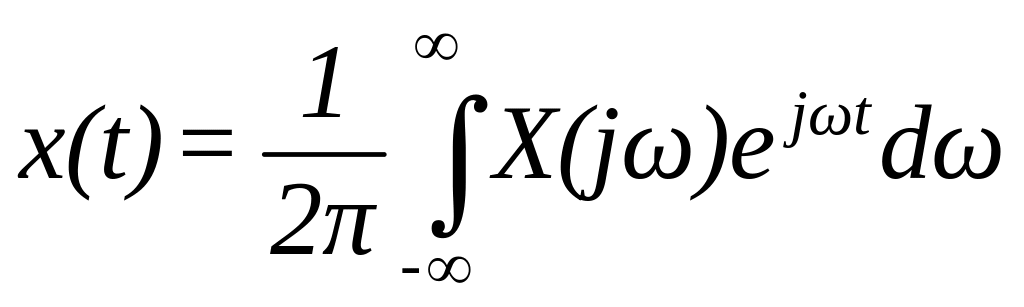
По формулі Ейлера можна визначити

Тоді ,

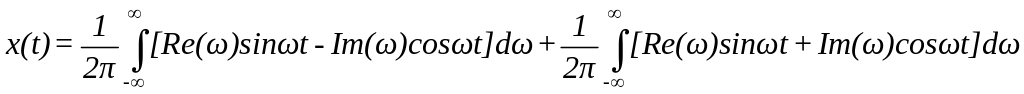тому що друга частина є непарною функцією від , то

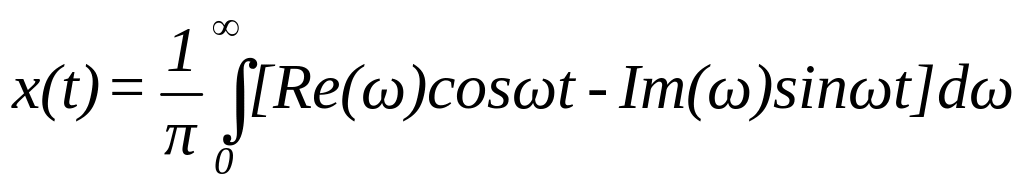
Тому що реальні сигнали при дорівнюють нулю, то права частина дорівнює нулю при від’ємних значеннях . Отже, поклавши , будемо мати

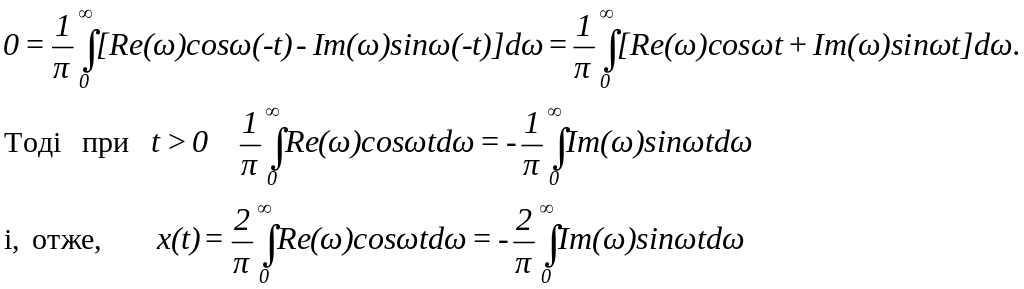(1.49)

Позначимо модуль зображення , a – аргумент ,

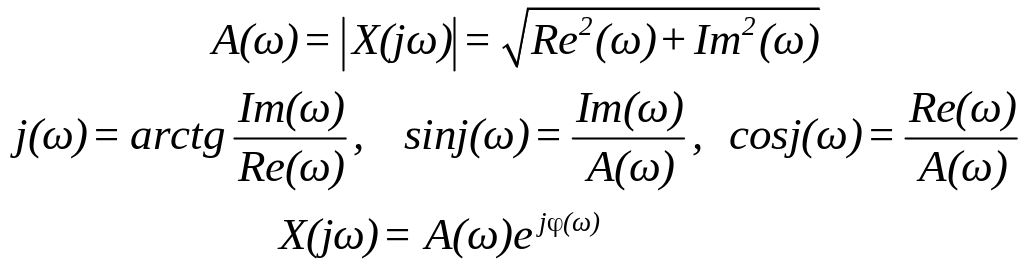(1.50)

Таким чином інтеграл Фур’є представляє сигнал як суму нескінченного числа елементарних гармонічних коливань. Множина таких частот утворює спектр сигналу.

Запишемо інтеграл Фур’є у комплексному вигляді

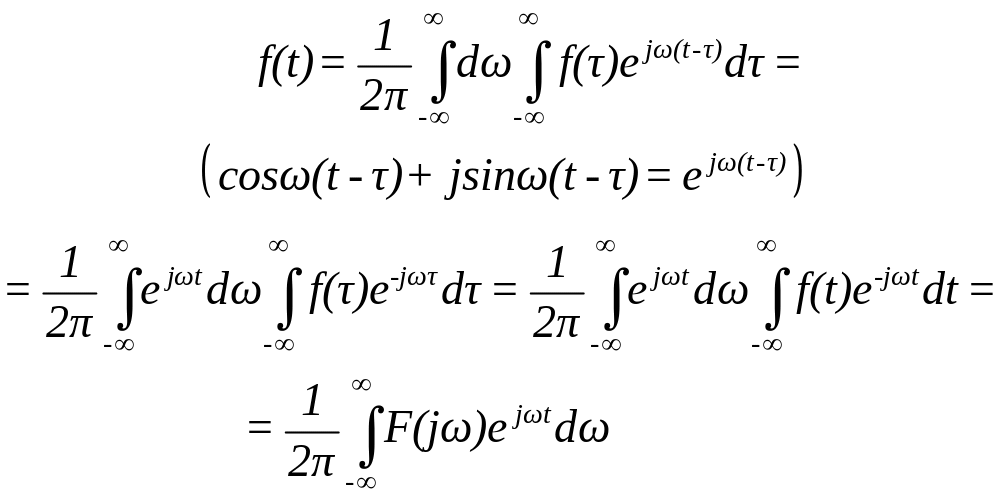₍₂₈₎

де 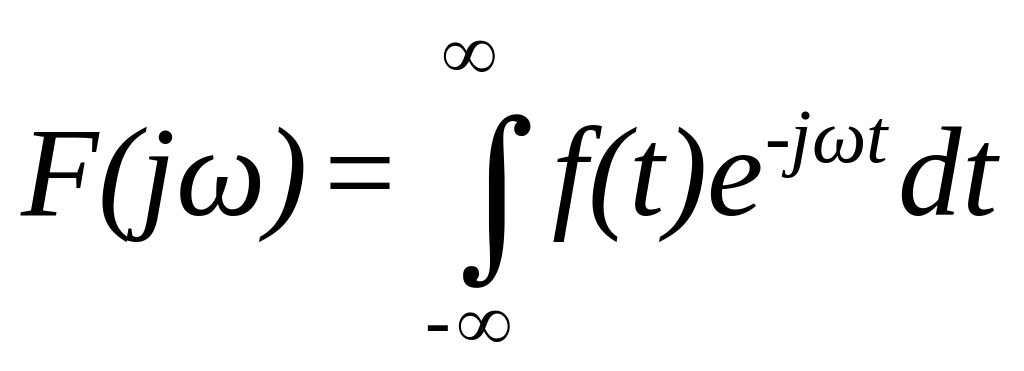виконує роль коефіцієнта ряду Фур’є.

Отже, функція зветься перетворенням Фур’є функції . Ця функція характеризує спектральний склад функції і є спектральною характеристикою або спектральною щільністю функції .

При цьому

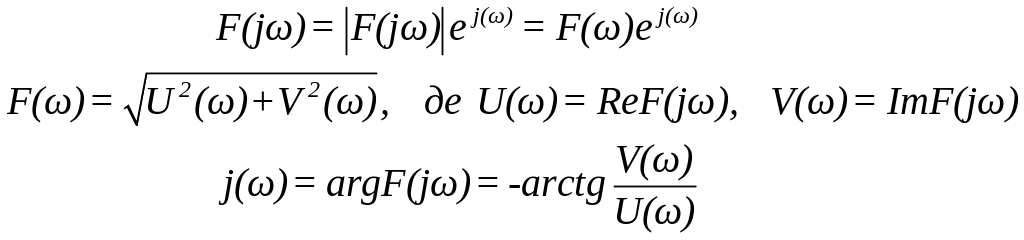
Відомо, що перетворенню Фур’є підлягають функції, які задовольняють умовам Дирихле та абсолютно інтегровані на осі часу.

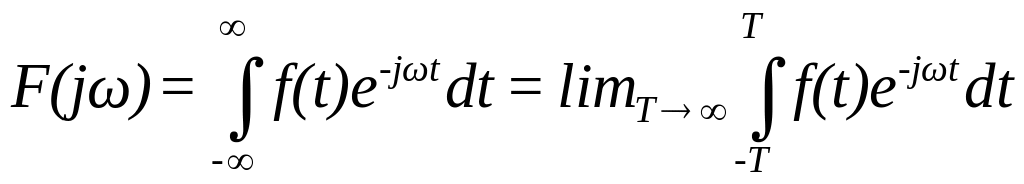
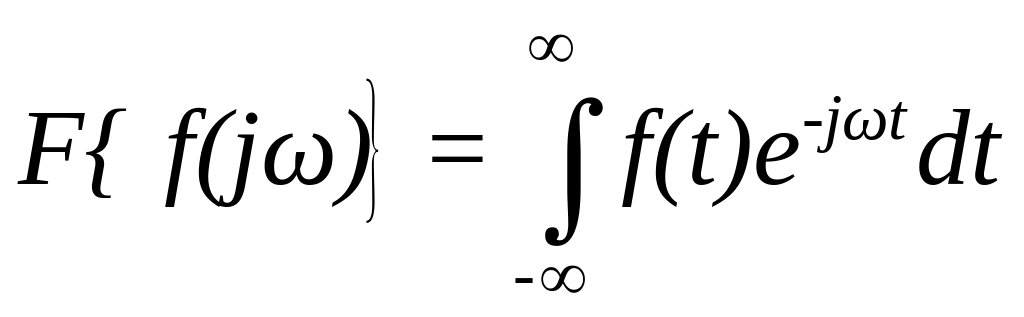
Формулу інтеграла Фур’є називають зворотним перетворенням Фур’є

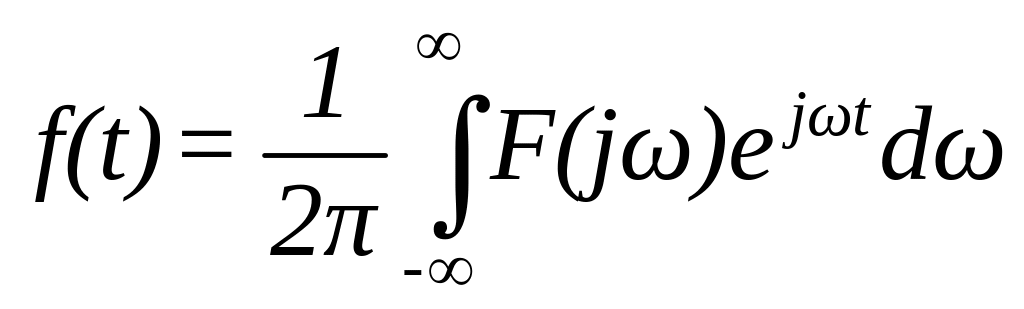(29)

У ряді задач автоматичного керування функція характеризує процес, який існує лише із деякого моменту часу, який приймається за нульовий. У цьому разі

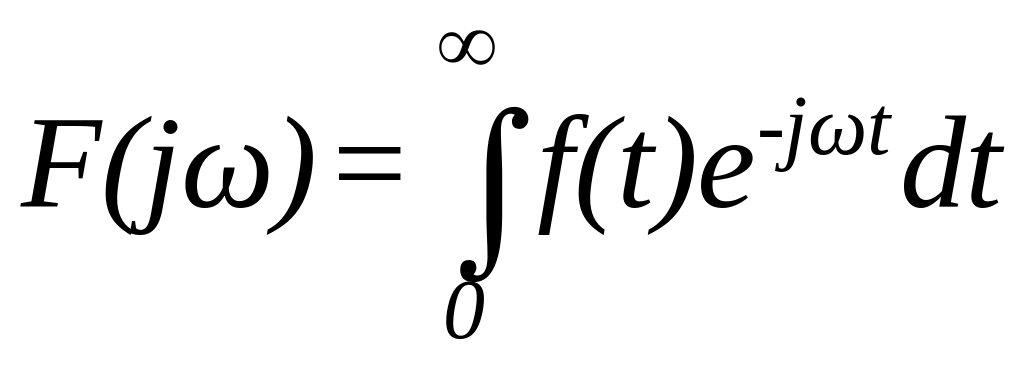, (30)

що визначає пряме однобічне перетворення Фур’є.

П 1.8

1. Застосування прямого однобічного перетворення Фур’є
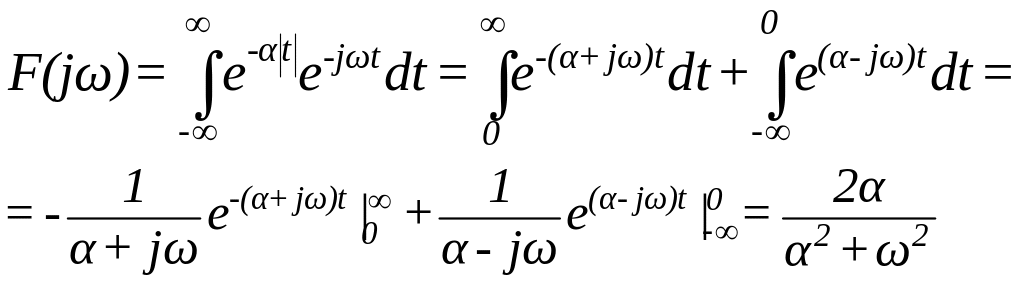