Цифрові системи автоматичного керування

Шпіт С.В.

Підручник

Зміст

Передмова

Розвиток мікропроцесорної техніки та мікроконтролерів дозволяє застосовувати цифрові пристрої для керування різноманітними об’єктами від простих дитячих іграшок. битової техніки до складних технологічних процесів, гнучких роботизованих лінії, літаків та космічних апаратів. За всю історію розвитку систем автоматичного регулювання та керування створено велику кількість різноманітних за своїм призначенням систем, які діють у різних областях людської діяльності та відрізняються одна від одної за об'єктами керування, фізичною природою сигналів, конструктивними особливостями, захищеністю від навколишнього середовища. Проте у теорії автоматичного керування при дослідженні системи проектувальника, в основному, цікавлять питання, зв'язані із збільшенням точності дії у всіх режимах функціонування системи що проектується. Застосування мікропроцесорів та мікроконтролерів у традиційних системах автоматичного керування звязано з принціпіальними змінами як їх структури, так і з можливостю застосовувати більш сучасні закони керування. Це обумовлено тим що існують багато чисельні явища, соціальні, економічні та біологічні системи, динаміка яких може біти описана дискретними моделями. Однією із суттєвих переваг цифрових контролерів є їх більша гнучкість у порівнянні з аналоговими регуляторами. Цифрові компоненти електронних схем часто більш надійні, більш компактні , ніж аналогові того ж самого призначення. Можливість перепрограмування мікропроцесорів та мікроконтролерів визначають можливість гнучкої оперативної перебудови як алгоритмів робоит системи керування, так і її структури, можливість адаптуватися до зміни умов роботи та впливів зовнішнього середовища. Використовування мікропроцесорів в системах автоматичного керування потребує розв’язання ряду задач, спеціфика яких обумовлена як розподіенням керування у реальному масштабі часу, так і цифравми характером обробки інформації про самі динамічні процеси та характеристики зовнішного середовища.

В основу написання підручника покладена багаторічна методична робота та практика викладання курсів «Теорія автоматичного керування» та «Цифрові системи керування» на кафедрі Технічної кібернетики Національного технічного університету України Київського політехнічного інституту . У зв’язку з переходом до нових учбових програм з обмеженим часом викладання складного теоретичного матеріалу ( 36 годин) автори були змушені відійти від традиційного викладання курсу , зосереджуючи увагу на основних методах опису цифрових систем автоматичного керування з одночасною їх ув’язкою з питаннями аналізу стійкості та якості цифрових систем автоматичного керування, з класичними та сучасними методами аналітичного конструювання цифрових регуляторів .

Підручник „ Цифрові системи керування” складається з чотирьох розділів:

Розділ І. Системні поняття теорії цифрових систем автоматичного керування.

Розділ ІІ Математичні моделі цифрових систем керування.

Розділ ІІІ Керованість та спостережливість динамічних об’єктів та систем керування

Розділ ІV. Методи синтезу цифрових регуляторів та систем керування.

Розділ V. Мікропроцесори в цифових системах автоматичного керування.

Кожний розділ включає термінологію, теоретичний матеріал по темам, до яких також включені практичні розрахунки та приклади постановок лабораторних досліджень. В основу підручника були покладені теоретичні та практичні матеріали, які увійшли до першого комп’ютерного навчального посібника „ Теорія автоматичного управління”, розробленого автором та рекомендованого Міністерством освіти і науки як навчальний посібник для студентів вищих навчальних закладів у 1998р., та до Пілотного проекту „Дистанційне навчання для підготовки бакалаврів за напрямком 6.051.001 «Метрологія та інформаційно-вимірювальні технології»” ;розділ «Теорія автоматичного управління». : сайт http://udec.utu-kpi,Kiev.ua/ , а також курс лекції «Цифрові системи керування»

Теоретичний матеріал підручника та приведені практичні розрахунки, які супроводжують теоретичний матеріал, а також постановки лабораторних досліджень та наданий до підручника лабораторний комплекс „SHS-ТАК” написані на основі багаторічного досвіду викладання курсу „Теорія автоматичного управління” на кафедрі „Технічної кібернетики” Національного технічного університету „Київський політехнічний інститут”. Розроблений автором лабораторний віртуальний комплекс „SHS-ТАК” забезпечує дослідження різноманітних неперервних, дискретних та нелінійних систем автоматичного керування як при детермінованих так і при випадкових впливах.

Підручник орієнтований на студентів технічних вузів, які ведуть підготовку бакалаврів для напряму 6.0914 “Системна інженерія” спеціальності 7.091402 “Гнучкі комп’ютеризовані системи та робототехніка ”, ” Комп’ютеризовані системи, автоматика і управління ”, „Автоматизація та комп’ютерно-інтегровані технології” та інші. Враховуючи, що теоретичний матеріал підручника значно більший, ніж необхідний згідно з відповідними навчальними програмами для підготовки бакалаврів за вказаними напрямками, підручник та віртуальний лабораторний комплекс „SHS-ТАК” може бути використаний магістрами, аспірантами та спеціалістами в області проектування та дослідження систем автоматичного керування різного призначення.

Автори виражають щиру вдячність колегам по кафедрі „Технічної кібернетики”, які своїми дружними порадами сприяли процесу написання підручника, а також студентам, що брали участь у створені лабораторного комплексу „SHS-ТАК” та підготовки розрахункових та практичних задач.

Цифрові системи автоматичного керування

Вступ

Теорія цифрового автоматичного керування як важливий розділ загальної теорії автоматичного керування є складовою частиною технічної кібернетики. Теорія цифрового керування є сучасним етапом розвитку теорії та практики автоматичного регулювання та керування, а також науковою базою для розв’язання задач комплексної автоматизації складних систем керування. Керування – це засоби зміни стану об’єкта, системи або процесу, за допомогою яких досягаються поставлені цілі. Цілями або задачами цифрового керування можуть виступати, наприклад, досягнення деякого бажаного стану об’єкта ( системи ) при дії на нього різного роду збуджуючих впливів; підтримка заданого степеню матеріального чи духовного комфорту членів суспільства при розв’язанні задачі розвитку його економіки та культури; визначення такого режиму роботи промислового підприємства, при якому досягається максимум продукції, що випускається, при мінімумі затрат. Якщо поведінка об’єкт визначається не тільки миттєвими (поточними) значеннями впливів на нього, але і залежить від їх попередніх значень, тобто об’єкт по своєї природі є динамічним, то його цифрова математична модель стає більш складною та буде описуватися на мові дискретних рівнянь. Отже, побудова цифрової математичної моделі явища що вивчається, процесу або об’єкта керування - це одна із наукових і методологічних основ, на базі яких цілеспрямовано об’єднюються зусилля спеціалістів, які працюють у галузі побудови сучасних складних систем. При вивченні процесів керування теорія цифрового керування як і загальна теорія автоматичного керування aбстрагується від природи та конструктивних особливостей складових частин систем керування, тобто замість реальних об’єктів розглядаються їх адекватні цифрові математичні моделі. Математична модель – це система математичних співвідношень, які описують об’єкт дослідження, процес або явище. Математичну модель класифікують по характеру математичних понять, які застосовуються для побудови моделі ( неперервні, дискретні, стохастичні, тощо ). Важливою характеристикою цифрової математичної моделі є степінь її адекватності реальному процесу та можливості її реалізації технічними засобами ( наприклад, на ЦОМ ). Математичною основою теорії автоматичного керування є знання основних законів фундаментальної фізики, хімії, математичного аналізу, теорії дискретних рівнянь, дискретного перетворення Лапласа, дискретного перетворення Фур’є , Z-перетворення, теорії імовірності та математичної статистики, теорії систем та прийняття рішень та сучасної філософії. Математичні моделі, які розглядаються у теорії цифрового автоматичного керуванні можуть бути представлені у вигляді системи дискретних рівнянь, описані у часової формі , у частотної області , через свої передаточні функції. Важливою особливістю вивчення питань аналізу цифрових систем керування є застосування сучасних методів дослідження, в основі яких лежить векторно матричний аналіз .

Теорія цифрового автоматичного керування досліджує три основних проблем: аналіз та синтез систем автоматичного керування, які по принципу керування поділяються на розімкнені системи керування та на замкнені системи, та особливість технічної організації цифрового керуванні на основі застосування мікропроцесорів та мікроконтролерів для реалізації складних алгоритмів керування. Якщо у перших керуючі впливи формуються у залежності від збуджуючих впливів з ціллю їх компенсації, то у замкнених системах автоматичного керування реалізується фундаментальна ідея зворотного зв’язку, відповідно якої відхилення дійсних значень регульованих координат від їх заданих значень використовується для формування керувань, які підтримують систему у бажаному стані. Крім цього замкнений принцип керування забезпечує властивості керованості і для нестійких об’єктів, що неможливо досягнути при розімкненому керуванні.

0днією з головних проблем у теорії автоматичного керування є проблема стійкості. Методи, які дозволяють якісно досліджувати деякі важливі властивості розв’язку звичайних диференційних рівнянь, не відшукуючи безпосереднє їх розв’язок, були розроблені у 1892р. математиком А.М. Ляпуновим. Ці методи складають основу теорії стійкості рішень диференційних рівнянь. На основі першого метода Ляпунова розглядаються необхідні та достатні умови стійкості руху реальної системи по її лініаризованому диференційному рівнянню замкненої системи. Другий ( прямий ) метод Ляпунова дозволяє по квадратичним формам рівняння Ляпунова та їх похідних оцінювати стійкість як лінійних так і нелінійних систем керування. Надаються критерії стійкості дискретних систем керування ( аналог критерію Гурвіця, критерій Шур – Кона, критерій Джурі, тощо). На основі принципу аргументу будуються частотні критерії стійкості дискретних систем керування ( критерій Найквіста, критерій Михайлова, визначення стійкості на основі логарифмічних частотних характеристик, тощо), а також систем з чистою затримкою. Важливою особливості цифрових систем керування є умови існування у системі періодичних режимів автоколивань , які обумовлені квантуванням сигналів, обмеженою розрядністю цифрового слова . При практичному проектуванні систем автоматичного керування стає питання впливу як параметрів системи так і її структури на стійкість , на методи зриву режимів , визначення запасів стійкості та областей стійкості.

Для теорії автоматичного керування 2-ої половини 50-60 рр ХХ століття характерна інтенсивна розробка методів синтезу систем автоматичного керування, які визначають структуру та параметри керуючих пристроїв на основі формулювання вимог до характеру збудженого руху керованого об’єкта при відомої його математичної моделі та діючих на об’єкт керування збудженнях. Важливу роль у постановці задач синтезу грає вибір критерію якості системи автоматичного керування. Але задача побудова міри якості повинна вирішуватися з умов спостережливості та керованості, тобто умов які накладаються на параметри динамічної системи. При цьому треба пам’ятати, що поняття спостережливості та керованості є внутрішньою власивістю системи та зберігаються при будь яких еквівалентних перетворюваннях її математичної модель.

Серед різноманітних методів синтезу, які розглядаються у теорії автоматичного керування, особисте місце займають методи синтезу інваріантних та автономних систем керування. Домінуючими у теорії автоматичного керування є методи синтезу, які основані на використанні інтегральних критеріїв оцінки якості, для яких підінтегральна функція використовується як квадратична функція від фазових координат та керувань на кінцевому або напівкінцевому інтервалі часу. Найбільш поширеними при розв’язанні цієї задачі є методи синтезу лінійних цифрових систем, тобто методи аналітичного конструювання цифрових регуляторів, які дозволяють знайти керування у вигляді явних функцій фазових координат, тобто визначити структуру та параметри керуючого пристрою.

В основу написання підручника покладена багаторічна методична робота та практика викладання курсів «Теорія автоматичного керування» та «Цифрові системи керування» на кафедрі Технічної кібернетики Національного технічного університету України Київського політехнічного інституту . У зв’язку з переходом до нових учбових програм з обмеженим часом викладання складного теоретичного матеріалу ( 36 та 28 годин відповідно) автори були змушені відійти від традиційного викладання курсу , зосереджуючи увагу на основних методах опису цифрових систем автоматичного керування з одночасною їх ув’язкою з питаннями аналізу стійкості та якості, з класичними та сучасними методами аналітичного конструювання цифрових регуляторів .

У першому розділі увагу зосереджено на системних поняттях теорії цифрового автоматичного керування. Розглядаються питання системного підходу до розв’язання проблеми створення математичної моделі досліджуємого технологічного процесу. Надається поширена класифікація систем керування з точки зору принципів побудови (принципу дії ), математичного опису оператора системи, характеру перетворення оператора у часі, наявності похибок у сталих режимах роботи, характеру перетворення у часі діючих у системі сигналів, кількості регульованих величин та каналів керування. Викладаються методи побудови математичних моделії об’єктів та систем керування, а також методи опису діючих детермінованих дискретних сигналів, лінійні перетворення Лапласа, Фур’є, Z – перетворення, w – перетворення та взаємозв’язки між ними.

У другому розділі надаються методи складання та розв’язання дискретних рівнянь системи керування . Визначаються поняття передаточної функції, особливості структурних перебудов у лінійних дискретних системах . Приводяться методи опису за допомогою часових та частотних характеристик та їх особливості для дискретних систем. Дається поняття змінних стану, методи визначення змінних стану , засоби розв’язання векторно – матричних рівнянь класичними та чисельними методами. Показується можливість розв’язання нелінійних векторно - матричних рівнянь чисельними методами. Кожний метод опису систем керування включає постановку задачі дослідження стійкості руху по Ляпунову, приводяться методики оцінки стійкості руху першим та прямим методом Ляпунова, дається поняття необхідних та достатніх умов стійкості . Надається особливості застосування алгебраїчних критеріїв стійкості Гурвіця, Шура-Кона, Джурі, алгебраїчного критерію стійкості на основі вивчення векторно – матричної моделі. Розглядаються особливості застосування частотних методів Михайлова та Найквіста для дослідження стійкості , приводяться особливості визначення стійкості по логарифмічним характеристикам. Розглядаються питання якості систем керування та методи її поліпшення. Даються прямі показники якості перехідних процесів, непрямі критерії оцінки якості такі як кореневі, частотні, інтегральні, методи визначення сталих похибок системи при дії детермінованих та випадкових впливах.

Третій розділ надає інформацію про сучасні методи проектування цифрових систем керування на основі поняття керованості та спостережливості динамічних об’єктів та систем керування. Приводяться поняття канонічних перетворень та відповідних форм досяжності, керованості, відновлюваності та спостережливості.

У четвертому розділі надаються засоби підвищення якості за рахунок зміни параметрів системи керування, включення місцевих зворотних зв’язків, методів інваріантності, включення корегуючих іифрових ланок, застосування типових законів керування та стандартних налаштувань цифрових регуляторів з точки зору мінімуму часу перехідних процесів. Розділ включає питання синтезу систем керування по заданим показникам якості. Приводяться поняття досяжності, спостережливості, керованості, ідентифікуємості. Надається методика синтезу за допомогою логарифмічних характеристик. Вводяться поняття цифрового регулятора, методів його реалізації, методів побудови систем з кінцевим часом перехідних процесів , методів побудови динамічних регуляторів в умовах повної та неповної інформації про змінні стану. Дається методика оцінки змінних стану системи керування та побудови на їх основі модальних регуляторів.

Пятий розділ складається із питань застосування сучасних мікропроцесорів та контролерів для реалізації практичних законів керування. Надається

Додатки включають типову навчальну програму курсу «Цифрові системи автоматичного керування», приблизний перелік лабораторних досліджень та методичні вказівки до них. До підручника надається системний диск з програмою лабораторного стенду «ТАК-SHS» та методичні вказівки до нього. Наводиться також обширна бібліографія.

Стор. Рис. Ф..

Розділ І. Системні поняттия теорії цифрових систем

автоматичного керування

Розглянемо узагальнену ієрархічну структурну схему керування технологічними об’єктами (рис.1). Можна виділити декілька рівнів керування [11].

На першому рівні виконується безпосереднє керування об’єктом по реально вимірювальним вихідним координатам за допомогою регуляторів з прямим або зворотним зв’язком. Сигнал, що задається є або постійним, або задається на одному із більших рівнів керування. Якщо об’єкт керування має одну керовану величину та один керуючий вплив , то об’єкт керування є одномірним. Якщо керування ведеться по декількам керованих змінних , то об’єкт вважається багатомірним.

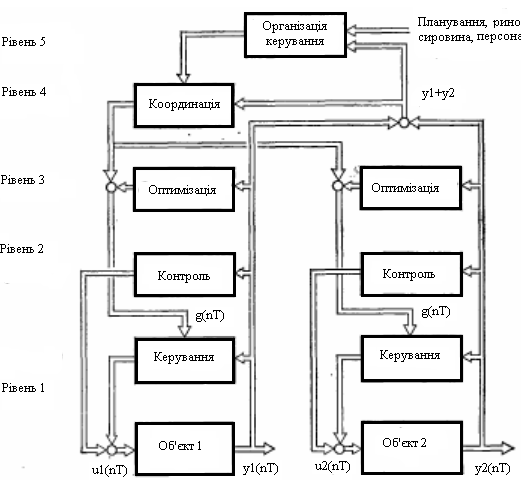
Рис. 1 Багатовівнева структура керування

На другому рівні виконується об’єднання операцій контролю за об’єктом керування. Виконується спостереження за визначеними характеристиками об’єкта, фіксуються перевищення заданих параметрів керування відносно допустимих значень, взначаються можливі аварійні ситуації та видаються відповідні сигнали попередження та автоматично включаються дії по забезпеченню умов безпеки.

До третього рівня відносяться процедури оптимізації, в результаті чого максимізується ефективність виконання цільової функції.

Якщо декілька об’єктів керування працюють сумісно, то їх координація виконується на четвертому рівні.

Самий верхній ( п’ятий) рівень призначено для організації керування. Вся система об’єктів організується з урахуванням вимог ринків, необхідної кількості сир’я та персоналу.

На кожному із розглянутих рівнях можуть застосовуватися керування як з розімкнутим так і замкнутим принципом керування. Якщо на всіх рівнях використовується замкнутий принцип керування, то поряд з безпосереднім керуванням об’єктами можна казати також про контури контроля, оптимізації та координації, тобто про багаторівневу структуру контурів керування.

Якщо до 1960р автоматичнее керування виконувалося із застосуванням аналогових регуяторів різноманітної конфігурації, а для контролю застосовувалися як аналогоів так і цифрові пристрої, а координація та оптимізація виконувалися операторами, то з появою цифрових обчислювателей почали змінюватися як структура так і функції автоматизованого керування.

Гнучкість програмних засобів значно розширює можливості реалізації складних алгоритмів керування, дає можливість практичного застосування сучасних методів теорії керування, дає можливість обирати найбільш ефективні алгоритми при розв’язуванні конкретних прикладних задач. Тому наступний курс « Цифрові системи керування» повинен дати студенту відповідь на наступні проблеми ( Рис. ):

1. Вивчення математичних методів опису дискретних процесів, методів побудови математичних моделій об’єктів керування , сигналів та змінних стану, форми оцінок динамічних процесів та станів об’єктів керування.

2. Вибор структури системи керуванн:

   • системи керування з одним входом та одним виходом,

   • системи керування з перехресними зв’язками,

   • багатомірні системи керування.

3. Розробка алгоритмів керування та їх реалізація за допомогою відповідних регуляторів, їх структури та параметрів, вибір найкращих з точки зору заданих показників якості процесів керування.

4. Синтез систем керування по заданим показникам якості

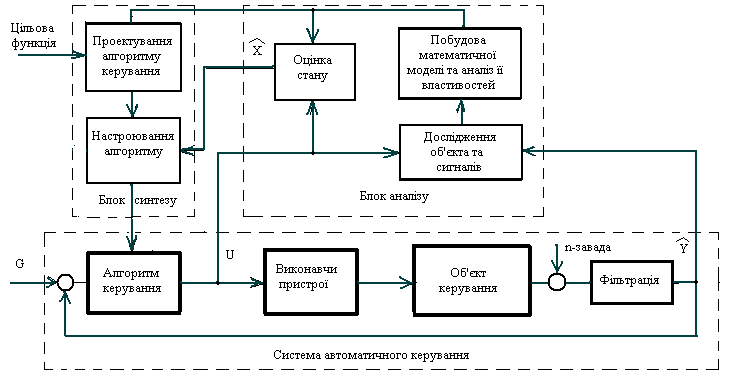
Рис. 2 Загальна схема проектування цифрових систем керування.

Для початкового періоду застосування ЦАС у сфері автоматизації технологічних процесів було характерним наближення до максимальної централізації задач, які розв’язувалися на одної та лише у окремих випадках на декількох керуючих ЦОМ. Коли почався серійний випуск мікропроцесорів, нових цифрових засобів автоматизації на основі мікроконтролерів , зя’вилась можливість знов перейти до децентралізованих методів керування за рахунок розподілу основної задачі по декільком спеціалізованим мікрообчисльвачам. Децентралізація дозволяє знизити вимоги до швидкодії окремих обчислювачем, спростити програмне забезпечення. Поява цифрових регуляторів з аналого-цифровими перетворювачами, цифрової вимірювальної техніки дозволило перейти до заміни традиційної аналогової техніки.

За всю історію розвитку систем автоматичного регулювання та керування створено велику кількість різноманітних за своїм призначенням систем, які діють у різних областях людської діяльності та відрізняються одна від одної за об'єктами керування, фізичною природою сигналів, конструктивними особливостями, захищеністю від навколишнього середовища. Проте у теорії автоматичного керування при дослідженні системи проектувальника, в основному, цікавлять питання, зв'язані із збільшенням точності дії у всіх режимах функціонування системи що проектується. З цієї точки зору вирішальне значення має поділ систем автоматичного керування за принципом організації систем керування, за метою керування, за характером оператора системи та за рядом інших ознак.

Будемо розглядати систему як реальний об`єкт або, як абстрактне поняття, яке складається з ряду елементів та існуючих зв`язків поміж ними, які характеризуються своїми властивостями, структурою, зв`язками з навколишнім середовищем.

При побудові математичної моделі системи необхідно враховувати фізичні параметри, які зв`язані з переходом процесу з одного становища до іншого, потрібно знайти форму подання взаємодії всіх елементів та зв`язків системи, розкрити причинно-наслідкові взаємозв`язки , тобто необхідно перейти до певної узагальненої форми подання явища котре вивчається, тобто до моделі процесу.

У процесі побудови причинно-наслідкових моделей потрібно відокремити модель самої системи керування , модель навколишнього середовища , модель зв`язків системи з навколишнім середовищем на вході та на виході , модель зв`язку виходу із входом , модель зв`язку виходу із входом впливу навколишнього середовища

(1.1 )

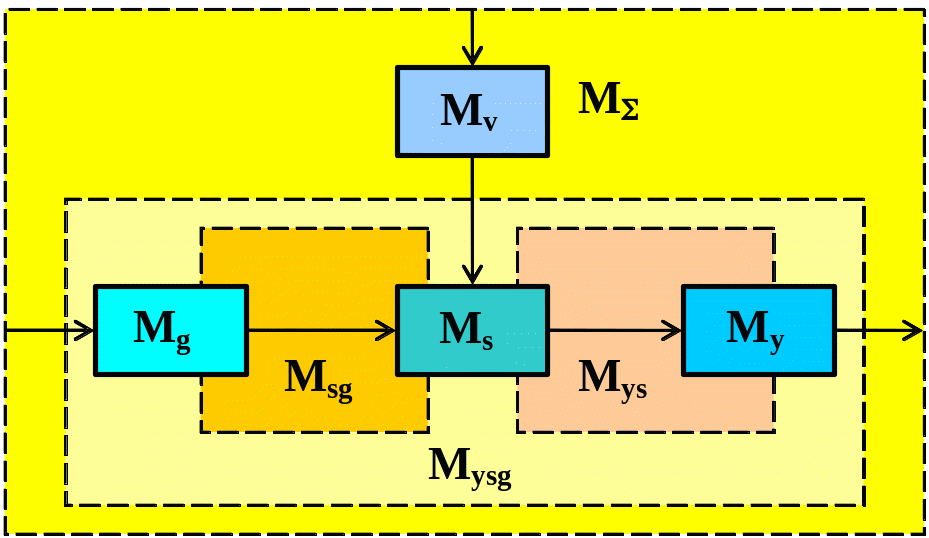
Рис 3 Модель розширеної системи

Отже, можна казати про загальну модель , як про модель розширеної системи :

(1.2)

Перехід від науково-технічної постановки задачі до моделі системи проходить через об`єктне та функціональне моделювання.

При об`єктному моделюванні символічно зображають елементи та функції системи, зв`язки між окремими елементами системи за рахунок речовини, енергії, інформації. Наслідком такого переходу є технологічна схема, яка орієнтована на найбільш суттєві явища у ході процесу. Як факти при цьому розглядаються конкретні конструктивні елементи.

Потім з`ясовується причинно-наслідкові взаємозв`язки, якісно описуються зв`язки між окремими вхідними та вихідними сигналами, установлюються кількісно-функціональні відношення у схемі проходження сигналів, тобто створюється функціональна модель системи, у якій можна абстрагуватися від потоків речовини та енергії. Як правило така процедура закінчується побудовою математичної моделі.

Треба пам`ятати, що методи створення системи керування та структури її моделі, повинні задовольняти ряду загальних принципів системного підходу по дослідженню складних систем керування.

1. Принцип однозначності – однозначне представлення сукупності основних властивостей для всієї чисельності моделей систем керування якої повинні дотримуватись на всіх рівнях моделювання систем керування, зв`язків з навколишнім середовищем, інтеграції окремих підсистем у складну систему.

2. Принцип не надмірності (не избыточности) – представлення деякої необхідної та достатньої сукупності основних властивостей системи для кожного етапу дослідження та проектування. Ліквідування надмірностей моделі на відповідному етапі доцільно здійснювати шляхом декомпозиції загальної задачі, поетапного дослідження окремих властивостей системи, шляхом перетворення деякої часткової інформації про окремі параметри у більш збільшувану інформацію о властивостях системи.

3. Принцип послідовного розкриття невизначеності – поетапне виявлення та формування властивостей системи керування, до чергових збільшень інформації, які дозволяють розв’язувати додаткові задачі по виявленню нових сукупностей властивостей досліджуваної системи.

Весь світ можна розглядати як систему систем. Але у такій сукупності неможливо досліджувати всі зв`язки. Тому досліджувана система повинна бути ізольована від навколишнього середовища, але при цьому у місцях розриву не повинна бути перекручення відповідних потоків енергії, речовини, інформації. Навколишнє середовище продовжує впливати на систему через відповідні вхідні величини, а вихідні величини системи впливають на навколишнє середовище.

Система складається із частин (елементів, підсистем), між якими існують істотні але різноманітні зв`язки та співвідношення. Складнiсть систем автоматичного керування визначається призначенням, задачами, властивостями об'єктiв керування, тобто об'ємом перероблюваної iнформацiї. Ступiнь складностi об'єкта керування зв'язана з числом контурiв, наявнiстю внутрiшнiх перехресних прямих та зворотних зв'язків, порядком диференцiйних рівнянь, розміром матриць, за допомогою яких описується динаміка системи. Знання особливостей математичних моделей, методiв та алгоритмiв рiшення технічних питань необхiдно iнженеру для успiшної постанови задач, для слушного формулювання початкових даних та iнтерпретацiї здобутих результатiв, при прийнятті рiшень про використання тих чи iнших компонентiв математичного забезпечення у процесi розробки проектних задач. Перед розробкою моделi фiзичного процесу необхiдно чiтко сформулювати цiлi та задачі керування, тому що моделi одного i того ж фiзичного процесу можуть мати мало загального, якщо вони розроблювались для рiзних цілей. Тому перед розробкою математичної моделi процесу необхiдно вирiшувати наступнi задачі:

1. Область дiї та межi вивчаємого процесу.

2. Глибина деталiзацiї фiзичного явища.

3. Фiзичнi обмеження та обмеження, які визначаються умовами безпечностi.

4. Характер керування у сталих та динамічних режимах роботи.

5. Необхiднiсть удосконалення моделi.

6. Змiннi стану та вiдомi змiннi керування.

7. Збуджуючі впливи, якi дiють на систему та некерованi змiннi.

Базою для розробки моделей процесу та опису дiючих сигналiв є основнi закони фiзики та хiмiї, дiючих у пневматичних, гiдравлiчних, теплових, механiчних та електричних системах. При трактуваннi основних законiв треба виходити iз єдиного системного пiдходу, що дозволяє iнженеру переходити вiд однiєї областi знань до iншої, наприклад, вiд гiдравлiки до електротехнiки, вiд теплотехнiки до механiки i т.п.

Запам'ятайте! Надто докладний математичний опис, який враховує неособливi для даної задачi властивостi елементiв, ускладнює рiшення задачi та може зробити її нерозв'язуємою.

Але надмірне спрощення задачi, прийняття необгрунтованих припущень недопустимо, тому що при цьому можуть бути упущенi iстотнi властивості процесiв у системi!

На кожному iєрархiчному рiвнi опису системи можуть використовуватися свої математичнi моделi, складнiсть яких погоджена з методом здобуття моделi та iз можливостями аналiзу! У теорiї автоматичного керування є достатньо розробленi iнженернi методи, якi дозволяють розв'язувати складнi задачі аналiзу та опису систем.

Аналiз систем позначає, що система керування вже побудована або визначено її математичний опис i потребується вивчити її характеристики та показники якості роботи у заданих умовах.

Термiн "синтез" вiдноситься до ситуацiї, коли задаються бажані вимоги до системи (показники якості), а необхідно знайти математичне рiшення задачі та визначена процедура цього рiшення, тобто необхiдно побудувати систему, яка задовольняє поставленим вимогам.

На першому етапi аналiзу виконується аналiз властивостей системи, вививчається структура цiєї системи, викриваються схеми відносин між елементами її структури. Пiсля виявлення всiх елементiв системи та встановлення структури їх зв'язкiв та вiдношень викривається суть кожного елементу, структурні вiдношення у серединi самих елементiв.

Існують декiлька пiдходiв до рiшення поставлених задач.

Перший пiдхiд базується на операторних методах, які мають справу iз перетвореннями у площинi комплексних змiнних S або Z, а також на методi кореневого годографу. При проектуваннi систем керування звичайно треба задовольняти ряду вимог, якi пред'являють до часових або частотних характеристик, до структури системи. Тому на цьому етапi аналiзу виконується оцiнка стiйкостi системи, здiйснюється вибiр структури та параметрiв, якi забезпечують стiйкiсть системи, оцiнюються запаси по пiдсиленню, по фазi, по показнику коливань та часу перехiдних процесів. Потім оцiнюється точнiсть системи при вiдпрацюваннi типових впливiв. Щоб задовольнити заданим вимогам виконується корекція параметрiв, корекцiя частотних та часових характеристик системи.

Другий пiдхiд, який часто-густо зветься аналiтичним, заснований на використанні оцінки якостi системи (iнтегральних квадратичних або середньоквадратичних похибок). При цьому проектування зводиться до розрахунку компенсуючих фiльтрiв.

Третiй пiдхiд до проектування систем полягає у визначеннi закону або стратегiї оптимального керування, при якому мiнiмiзується або максимiзується деяка сукупнiсть критерiїв якості. При цьому синтезуються закони керування, якi визначають керуючі впливи у виглядi функцiй координат стану об'єкта, що у результатi приводить до систем iз зворотними зв'язками.

Треба враховувати, що реальнi системи керування у більшості випадків є нелiнiйними. Тому для аналiзу та синтезу систем автоматичного керування бажано перейти до лiнеаризованих методiв, які використовують добре розробленi iнженернi методи проектування та розрахунку лiнiйних систем. У випадках, коли неможливо здiйснити операцiї лiнеаризацiї, тобто коли система буде суттєво нелiнiйною, методи, які пристосовані для розрахунку лiнiйних систем, стають недоцiльними. В цих випадках використовуються частинні методи аналiзу нелiнiйних систем , тому що в наш час загальних пiдходiв до їх розрахунку немає. При цьому кожний конкретний випадок потребує своїх методів для оцінки властивостей нелiнiйних систем та вибору необхiдних параметрiв.

1.1 Класифікація цифрових систем автоматичного керування по методу використання цифрової обчислювальної машини цом ( мікропроцесорів мп, мікроконтролерів мк ) для цілії керування.

Швидкість дії цифрових систем керування процесами прискорює обчислення та обробку інформації, дозволяє здійснювати оптимальне керування процесом у цілому, сприяє накопиченню даних, забезпечує можливість використовувати реєстрацію та проводити обробку даних, здійснювати діагнозування процесу та прийняття рішень.

Розглянемо основні функції керування процесами:

1. Обробки даних та спостереження за ними.

2. Безпосереднє та програмне керування.

3. Оптимальне та адаптивне керування.

Суть обробки даних та спостереження за ними у ході процесу керування можна пояснити схемою (Рис.4). Система збору даних готує у цифровій формі дані вимірювання для ЦОМ, яка видає оператору свідчення про ключові змінні процесу та заповнює робочий формуляр зміни поточними даними, звільнює оператора від рутинних операцій. Автоматичні регулюючі пристрої виконують роль органів керування у допоміжних ланках, а головним контуром керування є оператор, що використовує ЦОМ, яка видає йому рекомендації для керування процесами.

Рис.4 Система збору та обробки даних

Оптимальне керування використовується з метою досягнення найкращих у певному розумінні показників процесу керування на підставі визначення оптимальних управлінь, які надають екстремальних значень цільовим функціям за умови діючих обмежень. При цьому ЦОМ керування процесом шукає розв'язок рішення оптимального керування та видає значення змінних процесу, які потрібні для оптимізації цільової функції (Рис.5). Оптимальне керування можна використовувати із зворотними зв'язками або без них.

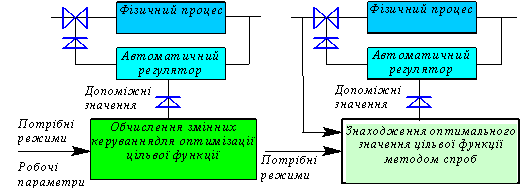
Рис.5 Принципи оптимального ккерування

У деяких випадках, якщо необхідно постійно слідкувати за параметрами процесу та пристосовуватись до їх зміни, уточнювати характеристики процесу, використовується адаптивне керування (Рис.6).

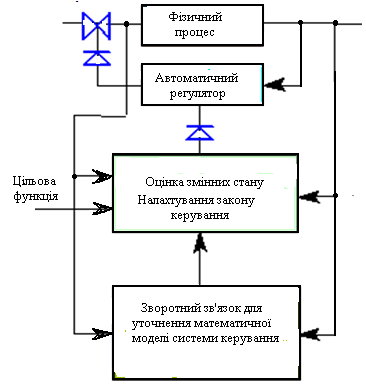
Рис. 6 Адаптивне керування

При безпосередньому керуванні (Рис.7) автоматичні регулюючі пристрої використовуються в одному контурі з ЕОМ, яка розподіляє їх роботу роздільно у часі. Програмне керування - це вироблення системою керування процесів певної послідовності процедур та керуючих дій, при якому керування здійснюється за допомогою автоматичних регуляторів шляхом подачі сигналів сталих значень на контрольовані точки або забезпечувати ввід керуючих впливів за допомогою подачі команд для пуску та зупинки окремих процесів.

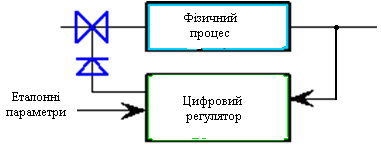
Рис.7 Система безпосереднього цифрового керування

Із теорії автоматичного керування відомо, що в системах керування використовуються централізоване, децентралізоване та комбіноване керування [7].

В системах з централізованим керуванням задача обробки діючих в системі сигналів про відповідні впливи та змінні стану виконується центральним цифровим пристроєм керування з ціллю формування керуючих впливів та видачі команд для їх виконання з урахуванням існуючих обмежень та умов безпеки. Узагальнена структура мікропроцесорної системи керування з централізованим керуванням показана на рис.8. Вона складається із обєкта керування (ОК), цифрового керуючого пристрою (ЦКП), ряду вхідних аналого-цифрових перетворювачів (АЦП), та ряду вихідних цифро-аналогових перетворювачів (ЦАП), сигнали з яких через пристрої перетворення та підсилювання (ППП) водаються як керуючі впливи на виконавчі механізми (ВМ)., які безпосередньо на об’єкт керування.

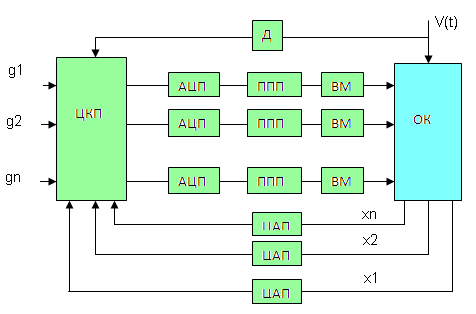
Рис. 8 Структура цифрової системи керування

з центральним керуванням

Якщо здійснюється керування складним багатовимірним об’єктом (прокатним станом, літаком, космічним апаратом, роботом, тощо ), тотака САК зветься зв’язаною. В цьому випадку загальну систему керування можна розглядати як сукупність одноконмурних систем керування, кожна з яких має своє програмне керування (ПК) та виконаві механізми ( Рис.9 ). Якщо локальні САК зв’язані між собою, то загална багатовимірна САК вважається зв’язаною. Якщо ж ПК буде видавати керуючі впливи таким чином, що зміна сигналів в однієї САК не буде впливати на характер роботи інших, то так система автоматичного керування вважається автономною.

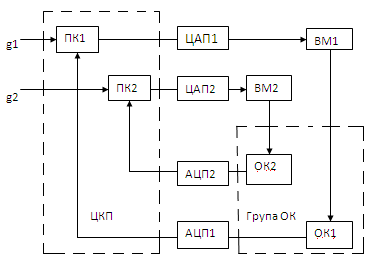
Рис.9 Керування групою незв’язаних об’єктів

В системах з децентралізованим керуванням в кожний контуркерування включається автономний цифровий пристрій, який виконує роль автономного ЦКП ( на рис. 10 позначається як МК), тобто мікроконтролер.

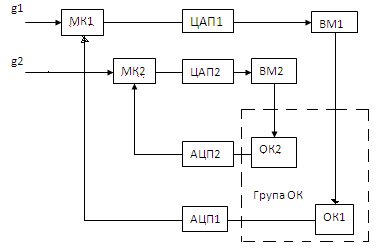
Рис. 10 Структура мікропроцесорної САК з децентралізованим керуванням

При цьому в таких системах керування центральний керуючий пристрій оба зовсім відсутний, або вводиться для виконання функції диспетчара. В цьому випадку система керування стає комбінованою.

По місцю включення мікропроцесора (мікроконтролера) у контур системи керування цифрові системи керування можна поділити на цифроаналогові, аналогоцифрові та цифрові.

До цифроаналогових систем відносяться системи в яких цифровий пристрій (ЦП) розташован безпосередньо перед аналоговою (неперервною) частиною. В цьому випадку на ЦП може покладатися задача не тільки прийняття рішень по розрахунку керуючого впливу, но і задача зв’язку з ЦОМ вищого рівня та видачі задаючого впливу. Структурна схема одномірної цифроаналогової системи представлено на рис.11

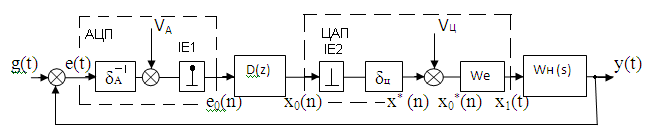
Рис.11 Структурна схема одномірної ЦАК

δ_^-1-коефіцієнт передачі АЦП, V_A-шум квантування, ІЕ-ідеальний імпульсний елемент першого роду, D(z)-передаточна функція ЦКП, ІЕ- ідеальний імпульсний елемент друого роду,δ_-коефіцієнт передачі ЦАП, V_Ц-шум квантування, We- передаточна функція екстраполятора, W_Н(s)- передаточна функція неперервної частини.

Аналого-цифровою системою (рис.12) назинається система автоматичного керування в якої перед цифровою частиною розміщені неперервні динамічні ланки.

Рис. 12 Cтруктурна схема замкнутої АЦС

В цьому випадку аналогово-цифрові системи не можливо розглядати як імпульсні фільтри із вхідними та вихідними сигналами у вигляді рішетчастих функції часу. Для таких систем не існує поняття передаточної функції і, отже, не може застосовуватися класичні методи аналізу у частотної області.