Лабораторная работа №1

Погрешности измерений физических величин

1 Цель работы

Знакомство с основными понятиями и схемами расчетов при измерениях физических величин. Усвоение навыков измерений и учета погрешностей на примере измерения плотности материала сплошного цилиндра.

2 Приборы и принадлежности

Микрометр, штангенциркуль, сплошной цилиндр.

Введение

На протяжении всего практикума по физике студентам необходимо применять теоретические сведения и многочисленные рекомендации по обработке экспериментальных данных и учету различных погрешностей при выполнении измерений, по оформлению отчетов, по построению графиков, по округлению числовых значений и т.д. И хотя данная работа и вводит студента в эту тематику, объем необходимой информации таков, что не может быть охвачен одной работой.

Много полезного студенты могут найти в методических указаниях «Введение в лабораторный практикум по физике» - сост. Д.Р. Бикпавленова, Волжский 2007.

3 Теоретическая часть

3.1 Погрешности измерений и схемы обработки результатов прямых и косвенных измерений

Погрешности измерения физических величин.

Практически во всех сферах человеческой деятельности приходится иметь дело с измерениями физических величин. Измерить физическую величину - значит сравнить ее с однородной (такой же в качественном отношении) физической величиной, принимаемой за единичную. Например, измерить скорость движения - это значить определить во сколько раз скорость этого движения больше скорости тела, движущегося со скоростью 1 м/с.

Полученные из опыта значения физической величины неизбежно отличаются от истинного значения этой величины, и эти отклонения называются погрешностями измерения физической величины. В связи с этим результаты измерений должны содержать в себе информацию как о числовых значениях физической величины, так и возможных отклонениях этих значений от истинных.

Измерения бывают прямые, когда измеряется непосредственно физическая величина, и косвенные, когда измеряемая физическая величина является функцией физических величин, подвергаемых прямым измерениям. Например, измерение длины (а), ширины (в), высоты (с) комнаты с помощью рулетки - это прямые измерения, а вычисление по результатам этих измерений объема комнаты по формуле V=а^.в^.с – это косвенное измерение объема комнаты.

Погрешности бывают систематические, случайные, приборные и погрешности, привносимые использованием табличных значений физических величин.

Схемы учета различных видов погрешностей

Систематические погрешности. Эти погрешности возникают в результате влияния на измерения какого-то постоянно действующего фактора (изогнута стрелка показателя прибора, наличие изъянов в шкале прибора, температура помещения и т.д.). Преодолеваются систематические погрешности путем проверки приборов, разработок более совершенных методик выполнения измерений, т.е. в принципе эти погрешности могут быть устранены, и поэтому при выполнении лабораторных работ систематические погрешности полагаются пренебрежимо малыми и не учитываются.

Случайные погрешности прямых измерений.

Пусть проведено n измерений величины Х, и получен ряд значений Х₁, Х₂,.., Х_n. В качестве наилучшего значения измеряемой величины принимают среднее арифметическое результатов измерений:

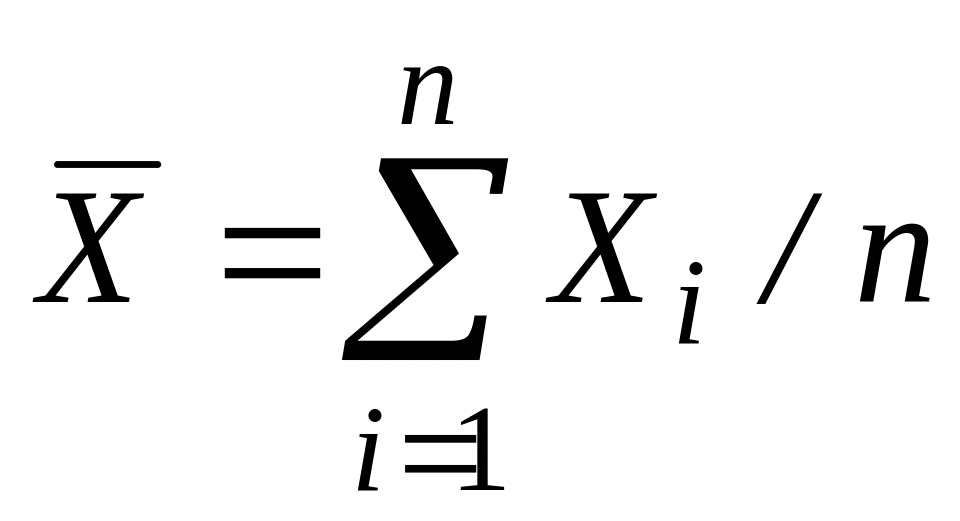. (1)

Затем вычисляют абсолютные погрешности отдельного (i-го) измерения:

. (2)

Для оценки случайной погрешности ΔX_сл используют среднюю абсолютную погрешность:

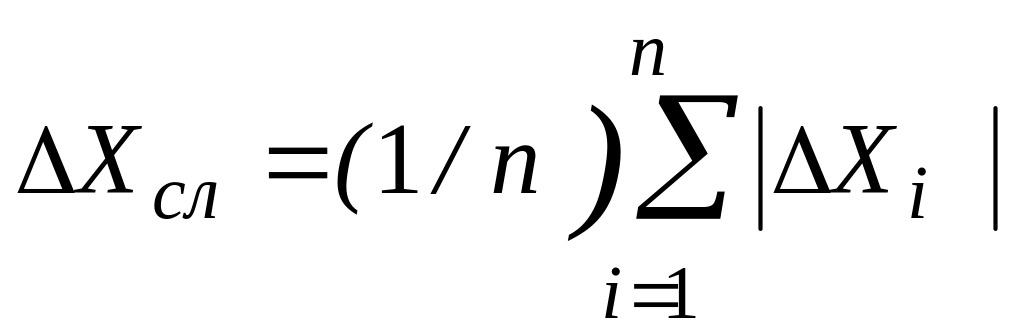. (3)

Приборные погрешности. Механические приборы (линейка, штангенциркуль, микрометр и т. д.) имеют приборную погрешность равную половине цены деления шкалы (с):

ΔХ_пр=С/2. (4)

Для электроизмерительных стрелочных приборов (амперметр, вольтметр и т.д.):

ΔХ_пр=к^.N/100, (5)

где N- максимальное значение шкалы прибора;

к - выраженный в процентах класс точности, который указывается на шкале прибора. Если класс точности на приборе не указан, то он считается равным 4,0.

Для некоторых приборов значение погрешности указано в паспорте прибора (и в описании л/р).

Полная (суммарная) абсолютная погрешность прямого измерения находится по формуле

. (6)

Если в этой формуле какая-либо из погрешностей окажется меньше другой хотя бы в два раза, то первая погрешность считается пренебрежимо малой и не учитывается.

Относительная погрешность измерения

. (7)

Форма записи итога прямого измерения величины Х

, . (8)

Все числовые значения в этой записи должны быть округлены.

Правила округления.

Сначала округляют абсолютную погрешность ΔX до 1-ой значащей цифры (считая слева направо). Затем округляют среднее значение в той же степени (т.е. до того же разряда), что и абсолютную погрешность. Относительную погрешность округляют до первой значащей цифры.

Пример:

До округления Х=0,38456±0,0002523

После округления Х= 0,3846±0,0003

ε= 0,0003^.100% / 0,3846=0,078≈0,08%

Пример:

До округления Х=26425,421±2758,418

После округления Х=26000± 3000

ε= 3000^. 100% / 26000=11,528≈10%

Полезная справка: в целях экономии времени в предварительных расчетах при сложении и вычитании исходные числа следует округлять, оставляя количество десятичных знаков на один больше, чем у числа с наименьшим количеством десятичных знаков;

при умножении, делении, возведении в степень, извлечении корня количество значащих цифр в числах следует оставить на одно больше, чем у числа с наименьшим количеством значащих цифр.

Пример:

Вместо 1,82+14,3673=16,1873

Следует сложить 1,82+14,37=16,19

Пример:

Вместо 83937^. 0,4=33577,8

Следует умножить 84^.10^3. 0,4=33,6^.10³

Погрешности табличных величин.

За абсолютную погрешность табличной величины (входящую в расчетную формулу) берется 0,5 единицы разряда последней значащей цифры.

Пример: плотность меди по таблице равна ρ=8,93^.10³ кг/м³. В этом случае Δρ=0,005^.10³ кг/м³

Таким образом ρ=(8,930±0,005)^.10³ кг/м³.

Схема обработки результатов косвенных измерений.

Пусть искомая величина Y является функцией непосредственно измеряемых величин Х₁, Х₂,.., Х_n

Y=f(Х₁, Х₂,.., Х_n. (9)

Сначала проводится обработка прямых измерений всех величин Х_i (см.2.2-2.7).

Затем рассчитывается среднее значение величины Y путем подстановки в формулу (9) средних значений величины Х₁, Х₂,.., Х_n:

. (10)

Для оценки относительной погрешности ε_y используется допущение:

ε_y= ε_хmax, (11)

где ε_хmax- максимальная относительная погрешность из погрешностей ε_х1, ε_х2 ..,ε_хn для величин Х₁, Х₂,.., Х_n.

Абсолютную погрешность ΔY косвенного измерения величины Y находят из формулы:

, т.е. . (11)

Окончательный результат измерения записывают в виде:

, ε_y=….% . (12)

Все числа здесь должны быть округлены по правилам (см 2.7).