3 Структурные средние величины

3.1 По результатам экзамена в группе определить аналитически и графически моду, медиану.

Т.к. ряд дискретный, значит Мо является вариант с наибольшей частотой.

Медиана – значение признака, стоящего в середине ранжированного ряда.

Оценка	Количество оценок	Накопленная частота	Мода	Медиана
5	12	15+12=27	5	9
4	9	6+9=15
3	2	4+2=6
2	4	4

3.2 На основе имеющихся данных о распределении предприятий города по объему выпуска продукции определить структурные средние величины. построить соответствующие графики.

Группа предприятий по объему выпуска, млн. руб.	Количество предприятий	Накопленная частота
До 40	30	30
40-50	32	62
50-60	11	73
60-70	20	93
70-80	12	105
80-90	24	129
90-100	23	152
Более 100	8	160

Мода:

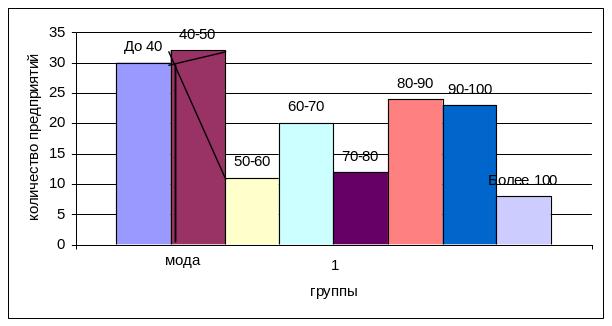
Рисунок 3 – Графическое нахождение моды

Медиана:

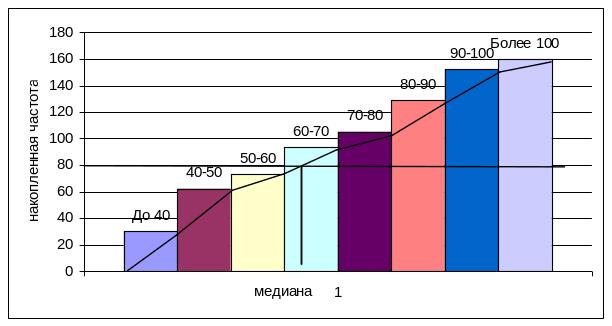
Рисунок 4 – Графическое нахождение медианы

4 Анализ вариационных рядов

1. Супермаркет имеет данные о покупках, совершаемые покупателями за определенный период. Рассчитать абсолютные и относительные показатели вариации. Сделать выводы.

Сумма покупки, руб.	Количество покупок, f	Середина интервального ряда, х	xf
До 100	46	50	2300
100-200	50	150	7500
200-300	62	250	15500
300-400	54	350	18900
400-500	48	450	21600
500-600	28	550	15400
Итого	288		81200

Показатели вариации:

Расчетные данные к показателям вариации.

Сумма покупки, руб.	Количество покупок	Отклонение цены от среднего значения	Квадрат отклонения	Взвешенное значение квадратного отклонения	Взвешенное отклонение по модулю
хi	fi	Xi-
50	46	-231,9	53798,2	2474718,4	10667,4
150	50	-131,9	17409,3	870466,8	6595
250	62	-31,9	1020,4	63267,7	1977,8
350	54	68,1	4631,6	250104,2	3675
450	48	168,1	28242,7	1355648,1	8066,67
550	28	268,1	71853,8	2011905,9	7505,56
Сумма	288			7026111,1	38487,4

Абсолютные:

- размах вариации R=x_max – x_min=550-50=500 руб.

- среднее линейное отклонение

- дисперсия

- среднее квадратическое отклонение

Относительные:

- коэффициент осцилляции

- линейный коэффициент вариации:

- коэффициент вариации

Т.к. коэффициент вариации достаточно большой (больше 33%), то исследуемая совокупность неоднородна.

4.2 Имеются условные данные о распределении предприятий города по размеру уплачиваемого налога на прибыль:

Группы по размеру уплачиваемого налога на прибыль, тыс. руб.	Число предприятий по городам
	Уфа	Казань	Самара
До 50	680	630	640
50-100	980	880	780
100-250	730	780	880
Более 250	590	600	590

Необходимо:

1) Вычислить: внутригрупповые дисперсии; среднюю из групповых дисперсий; межгрупповую дисперсию; общую дисперсию.

2)Проверить расчеты с помощью правила сложения дисперсий.

2) Оценить связь между группировочным и результативным признаками.

Группы по размеру уплачиваемого налога на прибыль, тыс. руб.	Уфа
хi
25	680	17000	8619090,4
75	980	73500	3838408,7
175	730	127750	1021974,5
325	590	191750	20723630,4
Сумма	2980	410000	34203104,0

Группы по размеру уплачиваемого налога на прибыль, тыс. руб.	Казань
хi
25	630	15750	8771091,1
75	880	66000	4068291,8
175	780	136500	799065,5
325	600	195000	19875911,45
Сумма	2890	413250	33514359,9

Группы по размеру уплачиваемого налога на прибыль, тыс. руб.	Самара
хi
25	660	16500	9438792,6
75	780	58500	3777101,7
175	880	154000	813922,8
325	590	191750	19203687,96
Сумма	2910	420750	33233505,2

Средний размер налога :

Средний размер налога по всем группам:

Внутригрупповая дисперсия:

Средняя из групповых дисперсий:

Межгрупповая дисперсия:

Общая дисперсия:

Правило сложений дисперсий:

Эмпирическое корреляционное отношение:

Выводы: Проверка с помощью правила сложения дисперсий показала, что расчеты проведены правильно. Эмпирическое корреляционное отношение показывает, что связь между группировочным признаком и результативным признаком очень слабая (согласно шкале Чеддока).

4.4. Для условий задания 4.3 выяснить общий характер распределения. Оценить соответствие эмпирического распределения теоретическому (нормальному закону распределения).

Группы по размеру уплачиваемого налога на прибыль, тыс. руб.	Число предприятий fi	хi	хi fi	fi
1	2	3	4	5	6	7	8
До 50	1950	25	48750	26657108,44	-1,09	0,7243	4579,46
50-100	2640	75	198000	11822714,81	-0,62	0,4581	2896,38
100-250	2390	175	418250	2615327,172	0,31	0,2661	1682,44
Более 250	1780	325	578500	59662478,38	1,71	0,9233	5837,66
Итого	8762		1243504	100757633,8			15003,9

= 141,9 тыс.руб. = 11449,5 тыс.руб.

Последовательно умножив const на величину j(t) для каждого варианта, получим теоретические частоты