Лабораторная работа № 2 Тема: Решение нелинейных уравнений методом половинного деления

Цель работы: Отделить корни нелинейных уравнений и уточнить их методом половинного деления с заданной точностью.

1. Теоретические сведения

1.1. Отделение корней нелинейных уравнений

Пусть дано уравнение

f (x) = 0, (1)

где f (x) определена и непрерывна в некотором конечном или бесконечном интервале [a,b].

Может понадобиться также существование и непрерывность первой и даже второй производной этой функции.

Всякое значение z, которое обращает функцию f (x) в нуль, является корнем уравнения 1.

В дальнейшем предполагается, что уравнение имеет только изолированные корни, т.е. для каждого корня существует окрестность, не содержащая других корней.

Приближенное решение нелинейных уравнений, т.е. нахождение изолированных корней состоит из двух этапов.

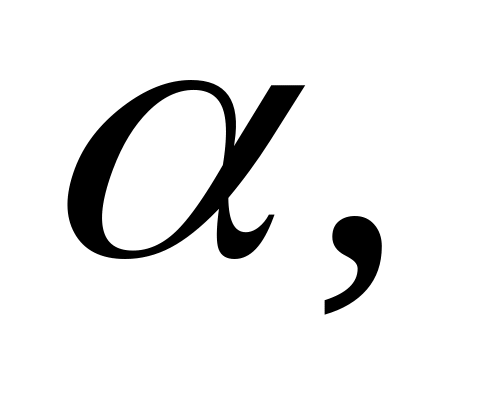
1. Отделение корней, т.е. установление возможно более тесных промежутков [ ] , в которых содержится только один корень.

2. Уточнение корней, т.е. доведение их до заданной точности.

Теорема 1.

Если непрерывная функция f (x) принимает значения разных знаков на концах отрезка [ ] , то внутри этого отрезка содержится по крайней мере один корень. Т. е. найдется на этом отрезке хотя бы одно число z, при котором f (z) = 0.

Корень будет единственным, если первая производная f (x) существует и сохраняет свой знак внутри интервала [ ].

Процесс отделения корней начинается с установления знаков функции f (x) в точках х=а и х=в. Затем определяются знаки функции в ряде промежуточных точек, выбор которых учитывает особенности функции.

Для отделения корней можно воспользоваться графическим методом его решения.

Теорема 2.

Для оценки точности полученного приближенного решения уравнения справедлива оценка

x – z | <= , (2)

где х – приближенное значение корня,

z – точное значение корня,

m₁ – наименьшее значение первой производной на отрезке [ ].

1.2. Метод половинного деления.

Дано уравнение f (х) = 0, где функция f (х) непрерывна на отрезке [a,b] и имеет разные знаки на концах этого отрезка, т.е. f (а) f (b) < 0. Для нахождения корня уравнения, принадлежащего отрезку [a,b], делим этот отрезок пополам.

Если окажется, что f ( ) = 0, то точное значение корня z = .

Если f ( ) 0, то выбирается та их половин исходного отрезка, на концах которой функция f (х) имеет противоположные знаки.

Новый суженный отрезок [a₁,b₁] снова делится пополам и т.д. В результате получаем на каком-то этапе или точный корень уравнения или бесконечную последовательность вложенных друг в друга отрезков [a₁,b₁], [a₂,b₂] ……………[a_n,b_n] таких, что

f (а_n) f (b_n) < 0, (3)

(b_n - a_n) = (b-a). (4)

Вычисления можно продолжать до тех пор, например, пока длина интервала, содержащего корень, не окажется меньше наперед заданного числа. Если задать интервал (b_n - a_n) при известном исходном интервале [a,b], то можно определить число n, т.е. необходимое число делений пополам для получения корня с заданной точностью. За конечное значение корня принимается середина интервала [a_n,b_n].