Лабораторная работа № 9 Тема: Решение систем нелинейных уравнений методом Ньютона

Цель работы: Найти корни системы нелинейных уравнений методом Ньютона

1. Теоретические сведения

Наиболее распространенным методом решения систем нелинейных уравнений является метод Ньютона, который обеспечивает более высокую скорость сходимости и имеет более широкую область сходимости. В основе метода лежит представление уравнений системы в ряд Тейлора.

+ члены более высоких порядков

…………………………………………………………………………… (1)

+ члены более высоких порядков

Если приращения таковы, что х₁ + , х₂ + и т.д. близки к корню, то левые части (1) обращаются в нули. Таким образом, задача сводится к отысканию таких совокупностей , при которых это достигается.

Если отбросить члены более высоких порядков малости, то задачу можно свести к решению систем линейных уравнений.

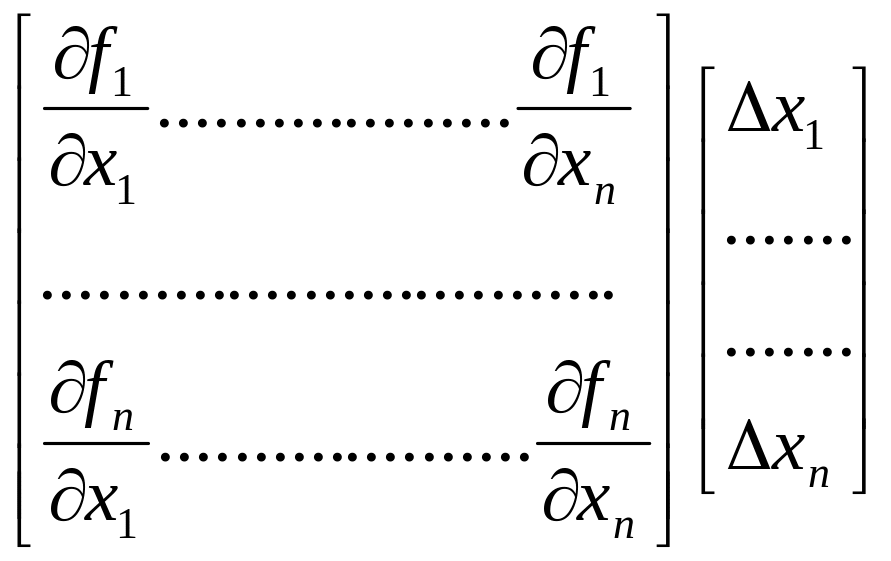= (2)

Матрица частных производных является матрицей коэффициентов при неизвестных, столбец - неизвестные, столбец в правой части – свободные члены системы линейных уравнений. Найденные значения в дальнейшем используются как поправки к текущему значению корней.

,

,

………………

.

Матрица частных производных и f_i вычисляются для текущих значений х_і , поэтому каждый получают новую систему линейных уравнений, решение которой новые значения добавок .

Вычисления продолжаются до тех пор, пока значения поправок не станут меньше заданной величины , которая определяет точность нахождения корней.

В методе необходимо выполнить большой объем вычислений, так как на каждом шаге вычислений приходится решать систему линейных уравнений.

Область сходимости вычислительного процесса в методе Ньютона приблизительно обратно пропорциональна степени сложности и числу уравнений системы, т.е. чем сложнее система и больше ее размерность, тем уже область сходимости.

При использовании метода важно удачно выбрать начальные приближения корней. Чтобы убедиться, что решение единственное, то надо взять несколько вариантов начальных приближений корней. Если во всех случаях будет получено одно и тоже решение, то оно является единственным, иначе, решений может быть несколько.

2. Порядок выполнения работы

1. Найти корни системы линейных уравнений методом Ньютона с заданной точностью, используя компьютерную программу из приложения.

2. В качестве начальных приближений неизвестных взять последовательно значения 1, 1; 10, 10; 100,100.

3. Выполнить проверки для всех вариантов начальных приближений подстановкой корней в исходную систему.

4. При выполнении проверку сохранять в вычислениях четыре знака в дробной части чисел.

3. Задание к лабораторной работе

3.1. Выбрать систему линейных уравнений в соответствии с вариантом.

1. 2.

3. 4.

5. 6.

7. 8.

9. 10.

11. 12.

13. 14.

15. 16.

17. 18.

19. 20.

21. 22.

23. 24.

25. 26.

27. 28.

29. 30.

3.2. Найти корни системы нелинейных уравнений методами итераций при заданных начальных прибдижениях корней с точностью 0,001.

3. Определить количество решений системы, если будут получены различные корни.

4. Показать, либо что все корни являются решениями системы либо только часть из них.

3.5. Оценить точность каждого решения по степени близости системы уравнений к тождеству при подстановке в нее значений корней.

3.5. Сраванить скорость и область сходимости для метода итераций (лабораторная работа № 6) и Ньютона.

3.6. Оформить отчет по лабораторной работе.

Приложение

program labrab9;

var

n,s: integer;

e: real;

x,y,x_p,y_p: real;

procedure fun;

var F,Fx,Fy,G,Gx,Gy,A,Ah,Ak,H,K: real;

begin

repeat

x_p:=x; y_p:=y;

writeln;

//Для вашого варианта надо изменить три следующие строки программы

//Выражения для первого и второго уравнений

F:=1/3*cos(y_p)+0.3-x_p; G:=sin(x_p-0.6)-1.6-y_p;

//Частные производные по х и у для первого уравнения

Fx:=-1; Gx:=-1/3*sin(y);

//Частные производные по х и у для второго уравнения

Fy:=cos(x-0.6); Gy:=-1;

// Вычисление новых приближений

A:=Fx*Gy-Gx*Fy;

Ah:=Fy*G-Gy*F;

Ak:=F*Gx-G*Fx;

H:=Ah/A; K:=Ak/A;

x:=x_p+H;

y:=y_p+K;

s:=s+1;

if (s<10) then

write('¦',s,' ¦')

else

write('¦',s,'¦');

write(x:8:4,'¦');

write(y:8:4,'¦');

until (abs(x-x_p)<e) and ((y-y_p)<e);

end;

begin

cls;

writeln ('Решение систем нелинейных уравнений метолом Ньютона');

writeln ;

write ('Введите точность e='); read (e);

writeln;

writeln ('Введите начальные приближения неизвестных ');

write ('x='); read(x);

write ('y='); read(y);

s:=0;

writeln('+--------------------+');

writeln('¦n ¦ X ¦ Y ¦');

writeln('¦--------------------+');

write('¦',s,' ¦');

write(x:8:4,'¦');

write(y:8:4,'¦');

fun;

writeln;

writeln('¦--------------------+');

writeln('Результаты решения');

writeln('x=',x:6:4,' y=',y:7:4,' Количество итераций = ',s);

writeln;

end.