2

МІНІСТЕРСТВО ОСВТИ І НАУКИ УКРАЇНИ

ХЕРСОНСЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

КАФЕДРА ІНФОРМАЦІЙНИХ ТЕХНОЛОГІЙ

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ

до виконання лабораторних робіт

з дисципліни

„Алгоритми та методи обчислень”

напряму підготовки 6.050102 „Комп’ютерна інженерія”

Херсон 2011

Требования к оформлению отчета

по лабораторной работе

1. Работа выполняется на листах формата А4.

2. Текст располагается только с одной стороны листа.

3. Используется шрифт Times New Roman, размер 14.

4. Межстрочный интервал одинарный.

5. Поля установить следующих размеров: верхнее и нижнее 2 см, левое 3 см, правое 1 см.

6. Нумерация страниц, начиная с первой в правом верхнем углу страницы.

7. Титульный лист использовать только предлагаемой формы (прилагается).

8. На титульном листе номер страницы не проставляется.

9. Весь ход выполнения лабораторной работы подробно поясняется, приводятся необходимые таблицы и рисунки.

10. Лабораторная работа представляется в бумажном и электронном вариантах.

11. Бумажный вариант помещается в файл или скрепляются с помощью скрепки.

Структура и содержание отчета

1. Название лабораторной работы.

2. Цель работы.

3. Теоретические сведения.

4. Задание к лаборатоной работе

5. Описание всех действий при выполнении лабораторной работы.

6. Текст компьютерной программы (если она используется в данной работе).

7. Результаты выполнения.

8. Анализ результатов (выводы).

Міністерство освіти і науки України

Херсонський національний технічний університет

Кафедра Інформаційних технологій

Лабораторная робота № 13

з курсу «Алгоритми та методи обчислень»

Тема «Интерполяционный многочлен Лагранжа

»

Виконав: Джумига М. Е.

студент груп 1 КСС

Перевірив:

к.т.н., доцент Лєпа Є.В.

Херсон 2011

Лабораторная работа № 1

Тема: Решение нелинейных уравнений графическим методом

Цель работы: Использовать средства электронной таблицы Exel для графического решения нелинейных уравнений.

1. Теоретические сведения

Решение нелинейных уравнений заключается в нахождении таких значений неизвестных, которые при их подстановке превращают уравнения в тождество. Для решения могут быть использованы различные методы, которые позволяют получить корни с заданной точностью.

Одним из таких методов является графический метод решения, который является простым и наглядным, но в силу графических построений не может обеспечить достаточную для практических целей точность. Но такой метод является чрезвычайно полезным для отделения корней при решении нелинейных уравнений (рассматривается в следующей лабораторной работе). Электронная таблица Exel, обладает удобными средствами для построения таблиц значений функций, входящих в решаемые уравнения, при заданных значениях аргумента, с последующим построением их графиков.

Пример 1. Решить графически нелинейное уравнение tg(x)-x/5=0 с точностью 0,1.

Решение.

1. Строиться таблица значений функции, входящую в левую часть решаемого уравнения для определенного диапазона изменения аргумента.

2. Диапазон изменения аргумента первоначально можно принять от -3 до 3 с шагом 1, последующим его изменением в случае необходимости. Это будет первая строка таблицы.

3. Во вторую строку таблицы в каждую ячейку под соответствующим значением аргумента вводится формула для вычисления функции tg(x)-x/5. Для того чтобы изменение значения аргумента сразу приводило к изменению значения функции, при записи формулы вместо значения аргумента необходимо ссылаться на адрес ячейки, в которой оно находится.

4. В результате будет получена таблица значений функции при заданных значениях аргумента.

-3	-2	-1	0	1	2	3
-0,022	2,585	-1,357	0	1,3574	-2,585	-0,743

5. Выделить всю таблицу и запустить мастер построения диаграмм. Тип диаграммы выбрать точечный. В результате будет получен график

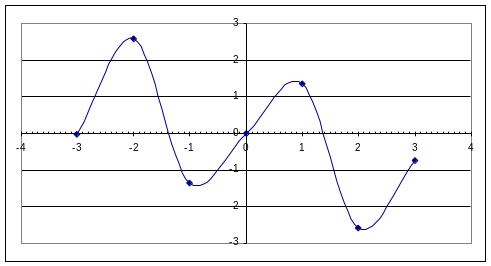
6. Точки пересечения кривой функции с осью абсцисс являются корнями исходного уравнения. В пределах заданного диапазона изменения аргумента это будут значения корней -1,4 и 1,4 с точностью 0,1.

7. Чтобы повысить точность определения корней, нанести на ось абсцисс промежуточные деления с шагом 0,1.Для этого необходимо выполнить следующие действия:

• установить указатель мыши на ось абсцисс и нажать правую кнопку.

• выбрать пункт меню Формат оси.

• выбрать вкладку Шкала.

• цену промежуточных делений установить 0,1.

• выбрать вкладку Вид.

• в списке Промежуточные выбрать переключатель внутрь.

Пример 2. Решить графически нелинейное уравнение tg(x)-x/5=0 с точностью 0,1, представив его в виде системы уравнений

tg(x)=0;

x/5=0.

Решение.

Строиться таблица значений функций, первая строка которой представляет изменение значения аргумента, а вторая и третьи строки соответственно изменение значений функций, входящих в систему.

-3	-2	-1	0	1	2	3
0,1425	2,185	-1,557	0	1,5574	-2,185	-0,143
-0,6	-0,4	-0,2	0	0,2	0,4	0,6

Выполняются все действия примера 1, в результате которых получен график

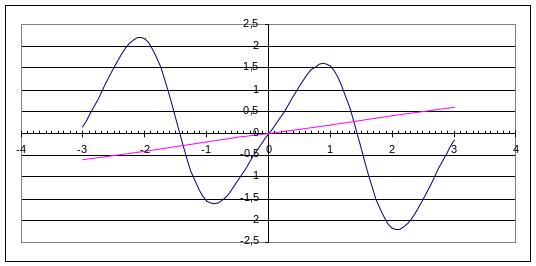
Из точек пересечения кривых опускаются (восстанавливаются) перпендикуляры и точки их пересечения с осью абсцисс являются корнями системы, а значит и корнями исходного уравнения.