Если первая из отброшенных цифр меньше 5, то оставшиеся десятичные знаки сохраняются без изменения.
Если первая из отброшенных цифр больше либо равна 5 и среди оставшихся отброшенных цифр есть ненулевые, то к последней оставшейся цифре прибавляется единица.
Если первая из отброшенных цифр равна 5 и остальные отброшенные цифры нулевые, то последняя оставшаяся цифра не изменяется, если она четная, и увеличивается на единицу, если она нечетная.
Теорема №1: Абсолютная погрешность суммы и разности двух приближенных чисел равна сумме абсолютных погрешностей слагаемых
Теореме №2: Относительная погрешность суммы и разности двух приближенных чисел равна:
Теорема №3: Абсолютная погрешность произведения и частного двух приближенных чисел находятся согласно формулам:
Теорема №4: Относительная погрешность произведения и частного двух приближенных чисел равна сумме относительных погрешностей его сомножителей:
Абсолютная и относительная погрешности для функции нескольких переменных, выражаются, формулами, соответственно:
Для функции одной переменной:
Задания для выполнения.
Округляя числа до трех значащих цифр, определить абсолютную и относительную погрешность приближения числа а=0,0001465.
Определить абсолютную погрешность следующего приближения числа а=0,7856 по его относительной погрешности (а)=0,8%
Найти абсолютную и относительную погрешности следующего приближенного равенства:
Зная абсолютную погрешность приближенного числа, определить сколько в этом числе верных значащих цифр а=0,00044, (а)=0,1*10-4
Пользуясь формулами для нахождения погрешности функции приближенных аргументов, найти абсолютную и относительную погрешность функции у=cоs(x).
Найти с указанной абсолютной погрешностью (у) значения следующего выражения
,
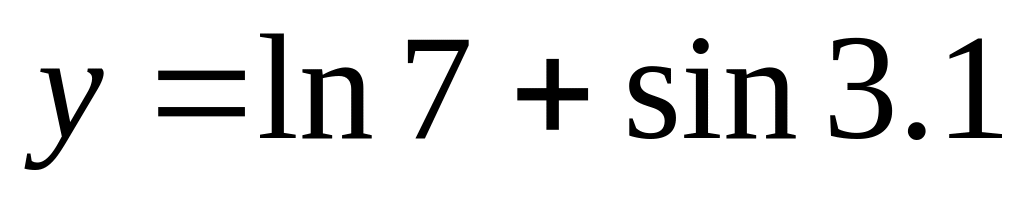(у)=0,810-5.Определить абсолютную и относительную погрешность объема призмы, если площадь основания S*=65,21 см2, а ее высота h*=10,28 при этом площадь основания и высота замерены с абсолютной погрешностью (S*)=(h*)=0,96. Определить приделы относительной погрешности.
Вычислить значения функции
,
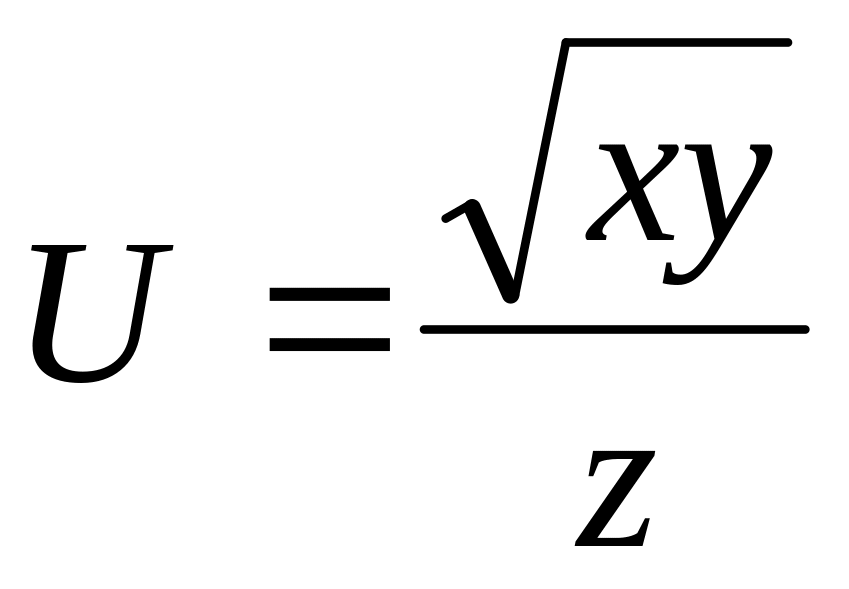ее абсолютную и относительную погрешность,
если х=47,1 у=8,87 z=5,052,
причем (х)=0,3
(у)=0,11
(z)=0,016
ВАРИАНТ №4. ПРАКТИЧЕСКАЯ РАБОТА №1.
ТЕМА: Действия с приближенными числами.
ЦЕЛЬ: Приобретение практических навыков работы с приближенными числами и выработка умения оценить погрешность, получающуюся при действиях с этими числами.
Основные понятия.
Определение 1: Абсолютной погрешностью приближенного числа а* называется
Определение 2: Относительной погрешностью приближенного числа а* называется
Определение 3: Значащими цифрами приближенного числа а называют все цифры в его записи, начиная с первого ненулевого.
Определение 4: Первые n значащих цифр приближенного числа называются верными, если абсолютная погрешность этого числа не превышает 0,5единиц разряда, соответствующего n-ой значащей цифре, считая слева на право. Остальные цифры называются сомнительными.
Правила округления:
Если первая из отброшенных цифр меньше 5, то оставшиеся десятичные знаки сохраняются без изменения.
Если первая из отброшенных цифр больше либо равна 5 и среди оставшихся отброшенных цифр есть ненулевые, то к последней оставшейся цифре прибавляется единица.
Если первая из отброшенных цифр равна 5 и остальные отброшенные цифры нулевые, то последняя оставшаяся цифра не изменяется, если она четная, и увеличивается на единицу, если она нечетная.
Теорема №1: Абсолютная погрешность суммы и разности двух приближенных чисел равна сумме абсолютных погрешностей слагаемых
Теореме №2: Относительная погрешность суммы и разности двух приближенных чисел равна:
Теорема №3: Абсолютная погрешность произведения и частного двух приближенных чисел находятся согласно формулам:
Теорема №4: Относительная погрешность произведения и частного двух приближенных чисел равна сумме относительных погрешностей его сомножителей:
Абсолютная и относительная погрешности для функции нескольких переменных, выражаются, формулами, соответственно:
Для функции одной переменной: