
- •Теория электрических цепей 1
- •Алматы 2007
- •Содержание
- •Введение
- •1Лекция 1.Элементы электрических цепей и электрических схем
- •3 Лекция 3. Основные законы и методы расчета линейных электрических цепей постоянного тока
- •Лекция 4. Метод эквивалентного генератора. Баланс мощностей
- •5 Лекция 5.Синусоидальный ток и основные характеризующие его величины
- •5.6 Синусоидальный ток в емкости
- •6 Лекция 6. Основы символического метода расчета цепей синусоидального тока
- •7 Лекция 7. Применение законов Кирхгофа, метода контурных токов и узловых потенциалов для расчета цепей синусоидального тока символическим методом. Векторные и топографические диаграммы
- •8.Лекция 8. Мощность в цепях синусоидального тока. Входные и передаточные характеристики
- •9 Лекция 9. Входные и передаточные характеристики
- •10 Лекция 10. Индуктивно связанные цепи
- •11 Лекция 11.Резонанс напряжений
- •12. Лекция 12. Резонанс токов
- •13 Лекция 13. Линейные электрические цепи при несинусоидальных периодических токах
- •14 Лекция 14. Четырёхполюсники. Уравнения передачи четырёхполюсников
- •15 Лекция 15. Характеристические параметры четырёхполюсника. Уравнения четырёхполюсника с гиперболическими функциями
- •16 Лекция 16. Электрические частотные фильтры и их классификация
- •17 Лекция 17. Пассивные реактивные lc-фильтры
- •Список литературы
- •Теория электрических цепей 1
- •050013, Алматы, Байтурсынова 126.
7 Лекция 7. Применение законов Кирхгофа, метода контурных токов и узловых потенциалов для расчета цепей синусоидального тока символическим методом. Векторные и топографические диаграммы
Цель лекции: познакомить с основными методами расчета цепей синусоидального тока, научиться строить векторные и топографические диаграммы.
7.1 Применение законов Кирхгофа, метода контурных токов и узловых потенциалов для расчета цепей синусоидального тока символическим метом.
7.1.1 Законы Кирхгофа.
Первый закон Кирхгофа в комплексной форме
|
(7.1) |
Второй закон Кирхгофа в комплексной форме
|
(7.2) |
Пример. Составим уравнения по законам Кирхгофа (рисунок 7.1) |
|
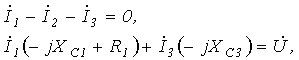
![]()
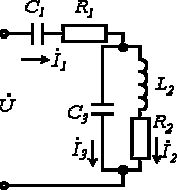
Рисунок. 7.1
7.1.2 Метод контурных токов
Пример. Составим уравнения методом контурных токов(рисунок 7.2)
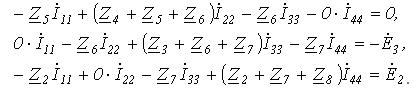
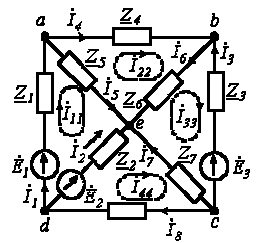 Рисунок 7.2
Рисунок 7.2
Решим
их относительно контурных токов и затем
по уравнениям, связывающим контурные
токи и токи ветвей, найдем последние.
![]()
![]()
![]()
![]() ,
,
![]() .
.
7.1.3 Метод узловых потенциалов
П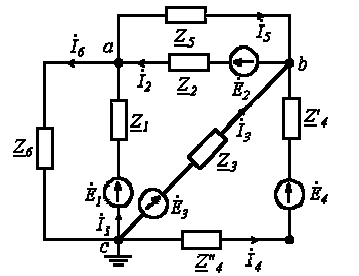 ример.
Составим уравнения методом узловых
потенциалов (рисунок 7.3).
ример.
Составим уравнения методом узловых
потенциалов (рисунок 7.3).
Рисунок 7.3
Составим
уравнения по методу узловых потенциалов
для узлов а и в. Потенциал узла
![]() =0.
=0.
![]()
![]() .
.
Токи ветвей выразим по закону Ома
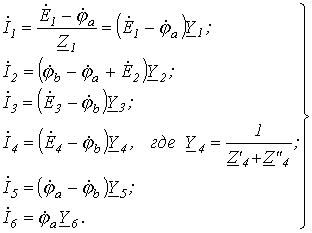 .
.
7.2 Векторные и топографические диаграммы
Совокупность радиус-векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называется векторной диаграммой. Векторные диаграммы наглядно иллюстрируют ход решения задачи. При точном построении векторов можно непосредственно из диаграммы определить амплитуды и фазы искомых величин. Приближенное (качественное) построение диаграмм при аналитическом решении служит надежным контролем корректности хода решения. При построении векторных диаграмм для цепей с последовательным соединением элементов за базовый вектор следует принимать вектор тока. Для цепей с параллельным соединением элементов за базовый вектор следует принять вектор напряжения, ориентируя относительно него векторы токов в параллельных ветвях. Для наглядного определения величины и фазы напряжения между различными точками электрической цепи удобно использовать топографические диаграммы. Они представляют собой соединенные соответственно схеме электрической цепи точки на комплексной плоскости, отображающие их потенциалы. На топографической диаграмме, представляющей собой в принципе векторную диаграмму, порядок расположения векторов напряжений строго соответствует порядку расположения элементов в схеме, а вектор падения напряжения на каждом последующем элементе примыкает к концу вектора напряжения на каждом предыдущем элементе.
В качестве примера построим векторную диаграмму токов, а также топографическую диаграмму потенциалов для схемы (см. рисунок 7.4).
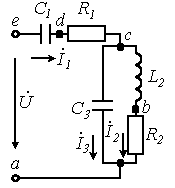 Рисунок
7.4
Рисунок
7.4
Параметры
схемы
![]()
![]()
![]()
![]()
При
данных параметрах и заданном напряжении
на входе схемы
![]() предварительно найденные значения
токов равны
предварительно найденные значения
токов равны
![]() ,
,
![]() ,
,![]() .
.
При построении векторной диаграммы зададимся масштабами токов и напряжений (см. рисунок 7.5). Векторную диаграмму можно строить, имея запись комплекса в показательной форме, т.е. по значениям модуля и фазы. Однако на практике удобнее проводить построения, используя алгебраическую форму записи, поскольку при этом вещественная и мнимая составляющие комплексной величины непосредственно откладываются на соответствующих осях комплексной плоскости, определяя положение точки на ней. Построение векторной диаграммы токов осуществляется непосредственно на основании известных значений их комплексов. Для построения топографической диаграммы предварительно осуществим расчет комплексных потенциалов.
Обозначив
на схеме ( рисунку 7.4) разнопотенциальные
точки и приняв потенциал точки а за
нуль(
![]() ),
определим потенциалы остальных точек
),
определим потенциалы остальных точек
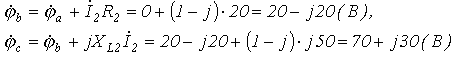
или
![]()
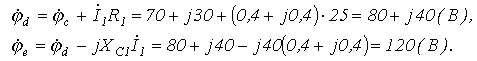
Таким
образом, в результате проведенных
вычислений получено, что
![]() ,
т.е равно напряжению U, приложенному к
цепи. В соответствии с полученными
результатами строится топографическая
диаграмма ( рисунок 7.5). В заключение
заметим, что векторы напряжений
ориентированы относительно точек
топографической диаграммы противоположно
положительным направлениям напряжений
относительно соответствующих точек
электрической цепи.
,
т.е равно напряжению U, приложенному к
цепи. В соответствии с полученными
результатами строится топографическая
диаграмма ( рисунок 7.5). В заключение
заметим, что векторы напряжений
ориентированы относительно точек
топографической диаграммы противоположно
положительным направлениям напряжений
относительно соответствующих точек
электрической цепи.
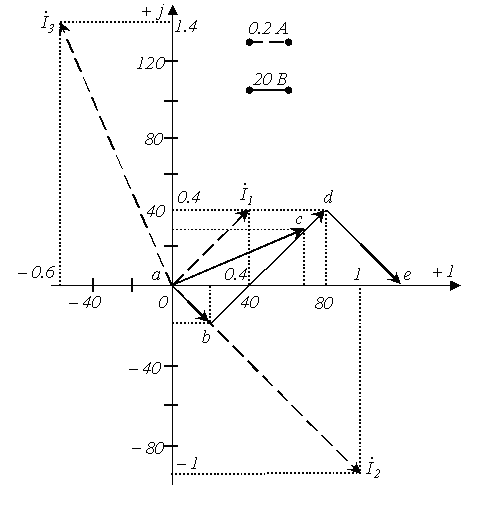
Рисунок 7.5
