3 Лекция 3. Основные законы и методы расчета линейных электрических цепей постоянного тока

Цель лекции: ознакомить с основными методами расчета линейных электрических цепей постоянного тока.

3.1 Законы Кирхгофа

Для написания законов Кирхгофа необходимо задаться положительными направлениями токов каждой ветви.

Первый закон Кирхгофа - алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю

. ( 3.1)

Токи, направленные от узла, условно принимаются положительными, а направленные к нему – отрицательными (или наоборот).

Второй закон Кирхгофа - алгебраическая сумма э. д. с. замкнутого контура равна алгебраической сумме падений напряжений в нём

. (3.2)

Направление обхода контура выбирается произвольно. При записи левой части равенства э. д. с., направления которых совпадают с выбранным направлением обхода, принимаются положительными, а э. д. с., направленные против - отрицательными. При записи правой части равенства со знаком плюс берутся падения напряжения в тех ветвях, в которых выбранное положительное направление тока совпадает с направлением обхода, а со знаком минус падения напряжения в тех ветвях, в которых положительное направление тока противоположно.

Пусть цепь состоит из N_в ветвей, имеет N_у узлов и N_т источников тока.

П р и м е н е н и е з а к о н о в К и р х г о ф а. Устанавливаем число неизвестных токов, равное N_в — N_т. Для каждой ветви задаются положительным направлением тока.

Общее число уравнений, составляемых по первому и второму законам Кирхгофа, равно числу (N_в — Nт) неизвестных токов. Число уравнений, составляемых по первому закону Кирхгофа, равно (N_у - 1). Число взаимонезависимых уравнений, составляемых по второму закону Кирхгофа

К =( N_в —N_т ) — (N_у - 1). (3.3)

При составлении уравнений по второму закону Кирхгофа следует выбирать независимые контуры, не содержащие источников тока.

3.2 Метод контурных токов

Метод основан на том, что ток в любой ветви цепи можно представить в виде алгебраической суммы контурных токов, протекающих по этой ветви. При пользовании этим методом выбирают и обозначают контурные токи (по любой ветви цепи должен проходить хотя бы один выбранный контурный ток). Общее число контурных токов равно К =( N_в —N_т ) — (N_у - 1). Рекомендуется выбирать N_т, контурных токов так, чтобы каждый из них - проходил через один источник тока. Эти контурные токи можно считать совпадающими с соответствующими токами источников тока J₁, J_{2, .} . ., J_NT, и они обычно являются заданными условиями задачи. Для них уравнения не составляют, но учитывают при составлении уравнений для других контуров.

Оставшиеся К =( N_в —N_т ) — (N_у - 1) контурные токи выбирают проходящими по ветвям, не содержащим источников тока. Для определения последних контурных токов по второму закону Кирхгофа для этих контуров составляют К уравнений в виде

R₁₁I₁₁ + R₁₂Ι₂₂ + … +R_1kI_kk+ … + J_nR_n = Е_11,

R₂₁I₁₁ + R₂₂Ι₂₂ + … +R_2kI_kk+ … + J_nR_n = Е_22, (3.4)

R_k1I₁₁ + R_k2Ι₂₂ + … +R_kkI_kk+ … + J_nR_n = Е_kk

где R_nn — собственное сопротивление контура n (сумма сопротивлений всех ветвей, входящих в контур n);

R_nl — общее сопротивление

контуров n и L, причем R_nl = R_ln.. Если направления контурных токов в общей ветви для n и L, совпадают, то R_nl положительно, в противном случае R_nl отрицательно;

Е_nn- алгебраическая сумма э. д. с., включенных в ветви, образующие контур n;

R_n — общее сопротивление ветви контура n с контуром, содержащим источник тока J_n.

3.3 Метод узловых потенциалов.

Он позволяет уменьшить количество уравнений системы до числа

m = N_у - 1. (3.5)

Сущность метода заключается в том, что вначале путем решения системы уравнений определяют потенциалы всех узлов схемы, а токи ветвей, соединяющих узлы, находят с помощью закона Ома.

При составлении уравнений по методу узловых потенциалов вначале полагают равным нулю потенциал какого-либо узла (его называют базисным).

Для определения потенциалов оставшихся (m = N_у —1) узлов составляется следующая система уравнений

(3.6)

Здесь G_ss – сумма проводимостей ветвей, присоединённых к узлу S;

G_sq – сумма проводимостей ветвей, непосредственно соединяющих узел S с узлом q ;

- алгебраическая сумма произведений э.д.с. ветвей, примыкающих к узлу S , на их проводимости; при этом со знаком плюс берутся те э.д.с., которые действуют в направлении узла S, и со знаком минус –в направлении от узла S;

- алгебраическая сумма источников тока, присоединённых к узлу S; при этом со знаком плюс берутся те токи, которые направлены к узлу S , а со знаком минус – в направлении от узла S.

Методом узловых потенциалов рекомендуется пользоваться в тех случаях, когда число уравнений будет меньше числа уравнений, составленных по методу контурных токов.

Если в схеме некоторые узлы соединяются идеальными источниками э.д.с., то число m уравнений, составляемых по методу узловых потенциалов, уменьшается

m = N_у – Nи – 1 (3.7)

где Nи – число ветвей, содержащих только идеальные источники э.д.с. В этом случае за нуль принимается один из узлов, принадлежащих ветви с идеальным источником э.д.с., тогда потенциал другого равен _{_} Е. Плюс, если двигаться по э.д.с., минус –если против.

3.5 Метод двух узлов

Для схем, имеющих два узла (например,узлы a и b), узловое напряжение U_ab определяется формулой

U_ab =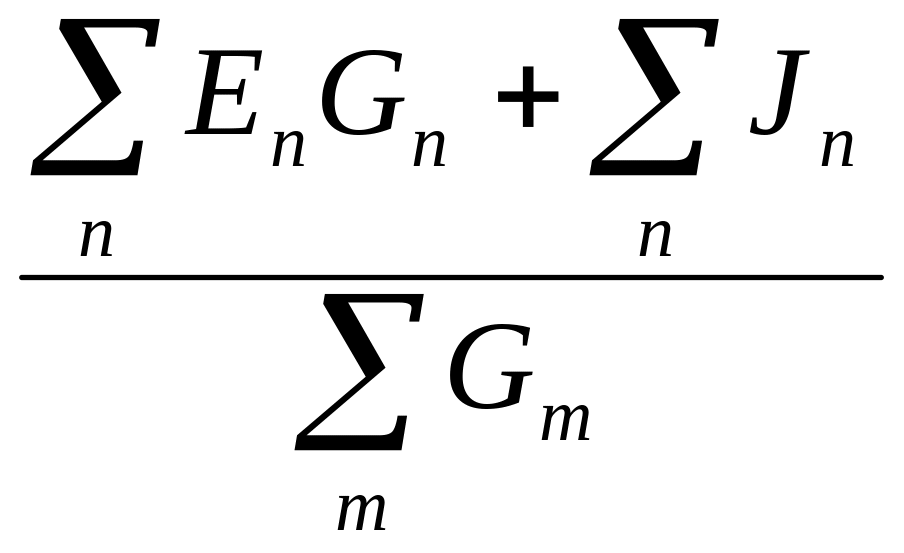 (3.8)

где ∑Ε_n G_n - алгебраическая сумма произведений э.д.с. ветвей (э.д.с. считаются положительными, если они направлены к узлу а, и отрицательными, если направлены от узла а, к узлу b) на проводимости этих ветвей;

J_n – токи источников тока (положительны, если они направлены к узлу а, и отрицательны, если направлены от узла а, к узлу b);

- сумма проводимости всех ветвей, соединяющих узлы а и b.

3.6 Метод замены нескольких соединенных параллельно источников э.д.с. одним эквивалентным

Если имеется несколько источников с э.д.с. Е₁, Е₂ … , Е _п и внутренним сопротивлениями R₁, R₂, … , R_n, работающих параллельно на общее сопротивление нагрузки R (рисунок 3.1, а), то они могут быть заменены одним эквивалентным источником, э.д.с. которого Е_эк, а внутреннее сопротивление R_эк (рисунок 3.1, б). При этом

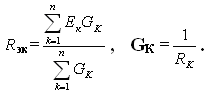(3.9)

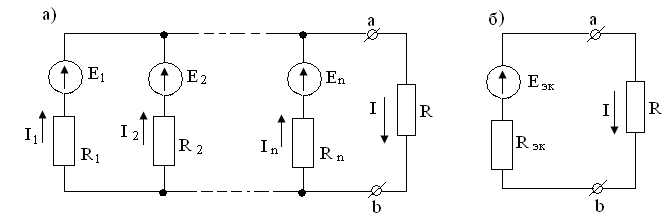
Рисунок 3.1

3.7 Метод замены параллельно соединенных источников тока одним эквивалентным

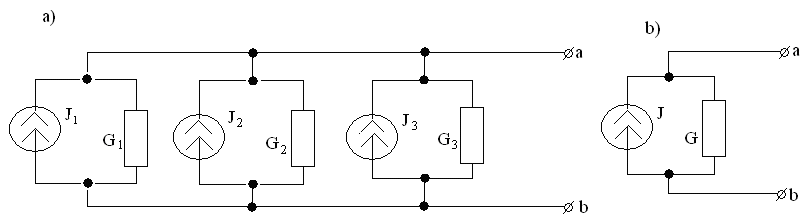
Если несколько источников тока с токами J₁ , J₂, … , J_n и внутренними проводимостями G₁, G₂, …, G_n соединены параллельно (рисунок 3.2,а), то их можно заменить одним эквивалентным источником тока (рисунок 3.2, б), ток которого J_эк равен алгебраической сумме токов, а его внутренняя проводимость G_эк равна сумме внутренних проводимостей отдельных источников

J =

G_эк= . (3.10)

Рисунок 3.2