4. Измерение времени т1

Импульсные методы ЯМР дают наиболее универсальный способ из­мерения времен Т₁ в широком диапазоне значений. Наиболее ши­роко применяемый способ – так называемая импульсная последовательность 180° –  – 90° (где  – промежуток времени, между соседними импульсами) – показан на рис. 5.

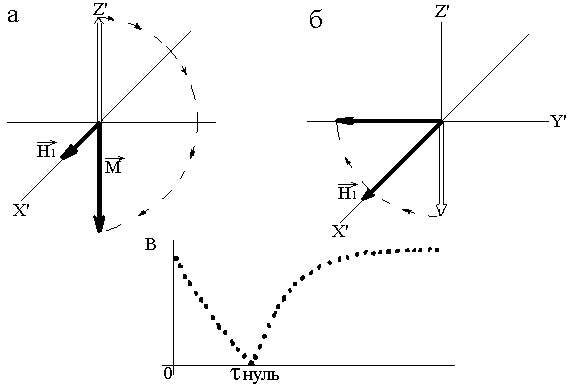
Рис. 5. Измерение Т₁ с помощью импульсной последовательности 180° –  – 90°

Сначала 180°-ный импульс инвертирует намагниченность вдоль оси . Далее происходит продольная релаксация, под действи­ем которой M_Z’ изменяется от значения –М₀, проходит через нуль и стремится к своему равновесному значению М₀. Если через время  после 180°-ного импульса к системе приложить 90°-ный импульс, также направленный по оси , то вектор намаг­ниченности повернется и окажется направленным по оси .

В результате будет наблюдаться сигнал свободной индукции, начальная амплитуда которого пропорциональна величине и, следовательно, величине M_Z’ в момент времени . Если теперь позволить системе вернуться к равновесию, для чего необходимо выждать, по крайней мере, время 5Т₁ (при 5Т₁ M_Z’ = 0,993М₀), и снова воздействовать на нее последовательностью импульсов 180° –  – 90°, но с другим значением , то можно найти скорость восстановления M_Z’. Количественно восстановление M_Z’ описывается уравнением Блоха:

_, (8)

Интегрирование уравнения (8) с начальным условием M_Z’ = –М₀ при t =0 дает:

, (9)

В эксперименте регистрируется абсолютное значение М:

, (10)

Это и есть функция, построенная на рисунке 5в. На практике вы­ражение (10) используется в преобразованном виде

, (11)

где A_ – начальная амплитуда индуцированного сигнала после 90°-ного импульса, приложенного в момент , а A_∞ – предельное значение A_ при очень длительном интервале между 180°-ным 90°-ным импульсами.

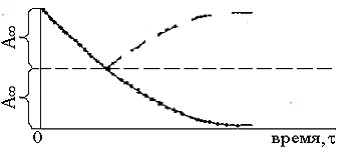
Рис. 6. Зависимость

На рисунке 6 приведена зависимость

Если переписать уравнение (11) в виде:

, (12)

то по наклону графика зависимости от  можно определить Т₁.

Из выражения (12) можно видеть, что при ₀= Т₁ln2≈ 0,69Т₁ A_=0. Поэтому Т₁ можно определить по временному промежутку между импульсами, при котором 90°-ный импульс не сопровождает­ся сигналом свободной индукции. Этот способ полезен для грубой оценки Т₁, но не годится для точных измерений.

Если Т₁ >> Т₂* , то Т₁ можно определить также с помощью импульсной последовательности 90° –  – 90° . В этом случае сиг­нал свободной индукции после первого 90°-ного импульса спадает до нуля значительно быстрее, чем M_Z достигает своего равновесного значения. Поэтому второй 90°-ный импульс позволяет определить значение M_Z в момент  как и с помощью последова­тельности 180° –  –90°. График зависимости ln (A_∞ ­^_ A_) от  снова является прямой линией, по наклону которой мож­но найти время Т₁.

5. Измерение времени т2 методом спинового эхо

В случаях, когда не выполняется условие 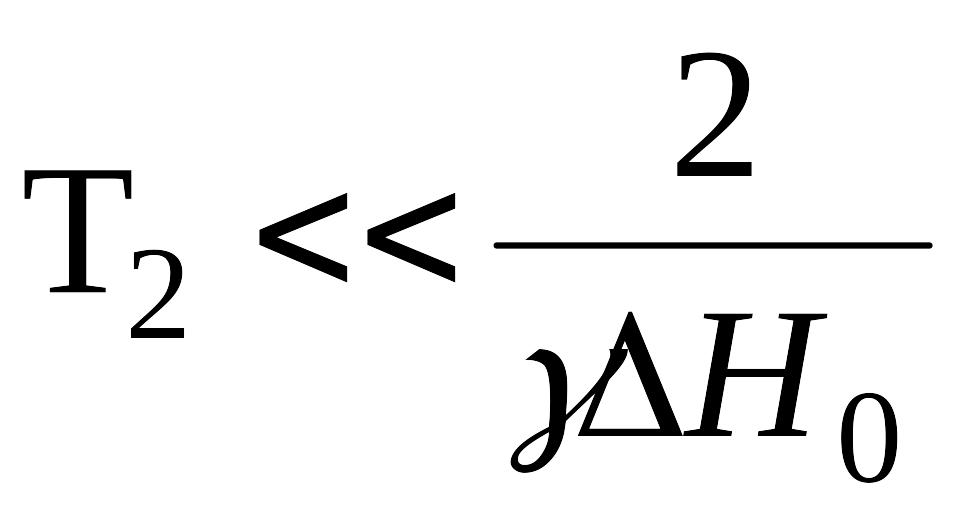, вклад неоднородности поля H₀ в скорость спада индуцированного сигнала не позволяет использовать это время спада Т₂ как меру Т₂. В этих случаях пользуется методом спинового эхо. Метод состоит в том, что на спиновую систему воздействуют импульсной последовательностью 90° –  – 180° и в момент времени 2 наблю­дают эхо-сигнал. На рис. 7, поясняющем сущность этого метода, показано поведение вектора намагниченности во вращающейся системе.

Рис. 7. Образование сигнала спинового эха при воздействии 90⁰-и 180⁰-ых импульсов

На рис. 7а показан поворот вектора намагниченности на 90° при включении поля вдоль положительного направ­ления оси . Полную намагниченность можно представить, как векторную сумму отдельных макроскопических намагниченностей , обусловленные ядрами, находящимися в разных частях образца и поэтому испытывающими воздействие внешнего поля несколько различной величины. Вследствие этого имеется целый набор частот прецессии при средней величине ₀, которую мы приняли за частоту вращения системы координат.

На рис. 7б начинают расходиться в веер, поскольку некоторые ядра прецессируют быстрее, а некоторые – медленнее, чем система координат. В момент времени  после 90°-ного импульса к спин-системе прикла­дывается 180°-ный импульс, также в направлении оси (рис. 7в). Под действием этого импульса каждый из векторов поворачивается на 180° вокруг оси . В результате, , которые движутся быстрее, чем система координат (на рис. 7б они изображены движущимися к наблюдателю, или по часовой стрелке, если смотреть со стороны ), будут, есте­ственно, продолжать двигаться быстрее, но на рис. 7г это движение направлено от наблюдателя.

В момент времени 2 все оказываются совпадающими по фазе и направленными вдоль отрицательной оси , как показано на рис. 7д. На рис. 7е видно, что продолжающееся движение заставля­ет их снова разойтись и потерять фазовую когерентность. Принудительная фазировка вызывает нарастание сигнала свободной индукции до максимума в момент времени 2 (рис. 7ж). Если бы поперечной релаксации не было, то амплитуда эхо бала бы такой же, как начальное значение сигнала свободной индукции после 90°-ного импульса. Однако все спадают в течение времени 2 вследствие естественных процессов, обуславливающих поперечную релаксацию, с характеристическим временем Т₂. Поэтому амплитуда эхо зависит от Т₂. Следовательно, Т₂ можно определить из зависимости амплитуды эхо от . Как и при измерении Т₂, для каждого значения  необходимо прилагать к образцу новую последовательность импульсов, а меж­ду ними выжидать время, достаточное для восстановления равновесия (не менее 5Т₁). Результат такого эксперимента показан на рис. 8.

Амплитуда эхо в момент времени t = 2 при промежутке между импульсами  пропорциональна выражению:

, (13)

Огибающая сигналов индукции после 90°-ного импульса и сигналов эхо описывает спад поперечной намагниченности:

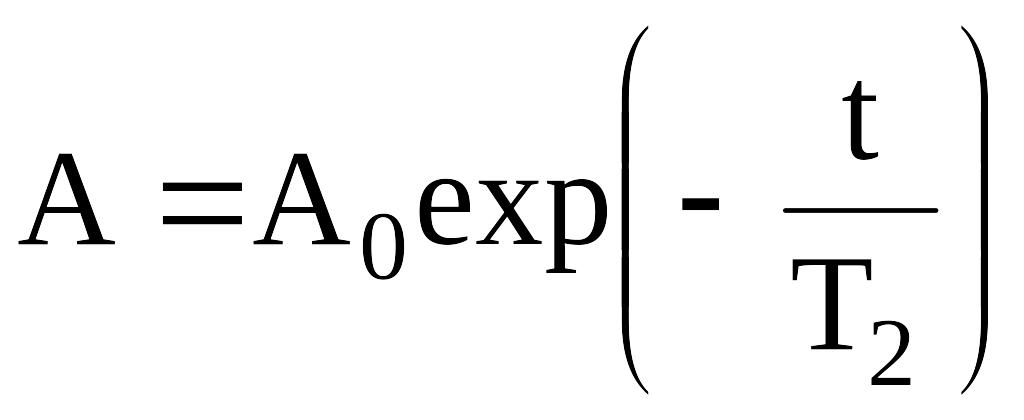, (14)

Из наклона графика lnA от t легко определить время Т₂.

Рис. 8. Результат эксперимента по спиновому эхо: а, б, в – результат воздействия 90°-  - 180° последователь­ности импульсов с различными значениями; г – объединенная картина.