14.2 Стационарные траектории динамической модели в матричной форме и их основные характеристики.

Упорядоченный набор векторов интенсивностей такой, что для любого номера имеет место равенство называется стационарным (точнее, квазистационарным) набором интенсивностей. Вектор называется элементом стационарного набора интенсивностей. Очевидно, набор интенсивностей является стационарным, если для любого номера имеет место равенство Здесь скалярные постоянные и положительны и вектор такой, что его октаэдрическая норма равна единице: Число и вектор называются основными характеристиками стационарного набора интенсивностей. Число называется коэффициентом постоянного пропорционального (т.е. сбалансированного) роста стационарного набора интенсивностей, вектор называется структурой стационарного набора интенсивностей. Если число то имеем случай постоянно растущего стационарного набора, если число то имеем случай собственно стационарного набора если число то имеем случай постоянно убывающего стационарного набора. Стационарный набор интенсивностей представляет собой набор сбалансированного развития (изменения) интенсивностей во времени. Все элементы стационарного набора интенсивностей расположены на луче натянутом на вектор (см. Рис. 14.1).

Для стационарной траектории интенсивностей ПС ДММФ имеем

или после сокращения на положительный множитель

(14.2.1)

В ерно, очевидно, и обратное. Если основные характеристики и стационарного набора удовлетворяет векторному неравенству (14.2.1), то этот набор есть стационарная траектория интенсивностей ПС ДММФ.

Из всех стационарных траекторий интенсивностей ПС ДММФ интерес представляют траектории с максимальным коэффициентом постоянного пропорционального роста интенсивностей, т.е. траектории максимального постоянного – пропорционального роста интенсивностей (ТрМсППРИ).

Для определения этих траекторий следует решить задачу квадратичного программирования

(14.2.2)
(14.2.3)
(14.2.4)
(14.2.5)
(14.2.6)

Решение этой задачи представляет собой основные характеристики ТрМсППРИ Основные характеристики определяются только матрицами и т.е. технологией ПС ДММФ. Задача (14.2.2) – (14.2.6) называется моделью максимального постоянного пропорционального роста интенсивностей (ММсППРИ). Теория максимального постоянного пропорционального роста интенсивностей (ТеМсППРИ) анализирует ММсППРИ и их оптимальные решения В ТеМсППРИ и в ММсППРИ цены не фигурируют.

Задачу квадратичного программирования (14.2.2) – (14.2.6) эквивалентна следующей задаче на

(14.2.7)

в которой дроби вида и не рассматриваются.

Переход от задачи (14.2.2) – (14.2.6) к задаче (14.2.7) осуществляется с помощью следующих простых рассуждений.

Векторное неравенство (14.2.3) переписывается в координатной форме

(14.2.8)

Получается система неравенств с одной неизвестной Решение этой системы имеет вид

(14.2.9)

где дроби вида и не рассматриваются, ибо они соответствуют неравенствам которые удовлетворяются при любых значениях Для отыскания остаётся найти

Задачи вида (14.2.7) относятся к классу задач наглядной оптимизации и в общем случае достаточно трудноразрешимы. Однако при задачи вида (14.2.7) легко решаются на основании элементарных геометрических соображений. Проиллюстрируем это обстоятельство на двух примерах.

Пример 14.2.1.

Матрицы и имеют вид

Имеем

Н арисуем эскизы графиков обеих дробно-линейных функций (см. Рис. 14.2). Очевидно, графиком функции является линия ибо при а при Из элементарных геометрических соображений достигается при Для определения следует решить уравнение которое сводится к квадратичному уравнению корнями которого являются числа

Выбираем корень который попадает в отрезок второй корень является посторонним.

Осталось определить коэффициент роста

Таким образом задача на максимин имеет решение

Пример 14.2.2.

Матрицы и имеют вид

Имеем

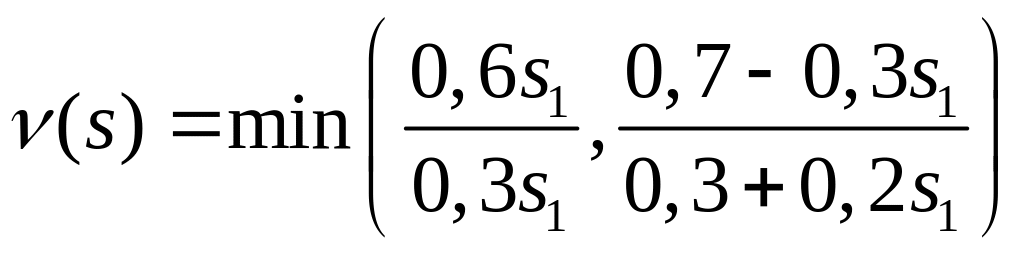Н арисуем эскизы графиков обеих функций (I) и (II) (см. Рис. 14.3). Из элементарных геометрических соображений графиком функции является множество, состоящее из ломаной линии (без точки и изолированной точки Точка не рассматривается, ибо при левая дробь имеет вид и поэтому не учитывается. Самой высокой точкой этого множества (графика функции является точка Следовательно, задача на максимин имеет решение Непосредственно проверяется, что

Упорядоченный набор векторов цен такой, что для любого номера имеет место равенство называется стационарным (точнее, квазистационарным) набором цен. Вектор называется элементом стационарного набора цен. Очевидно, набор цен является стационарным, если для любого номера имеет место равенство Верно и обратное. Здесь скалярные постоянные и положительны и вектор такой, что его октаэдрическая норма равна единице: Число и вектор называются основными характеристиками стационарного набора цен. Число называется коэффициентом постоянного пропорционального (т.е. сбалансированного) падения стационарного набора цен, вектор называется структурой стационарного набора цен. Если число то цены падают в реальном времени и растут в обратном времени, если число то цены постоянны (случай истинно стационарного набора цен если число то цены растут в реальном времени и падают в обратном времени. Стационарный набор цен представляет собой набор сбалансированного развития (изменения) цен во времени.

К вопросу о рациональности рассмотрения цен, падающих в реальном времени, мы вернёмся в следующем параграфе 14.3.

Все элементы стационарного набора цен расположены на луче натянутом на вектор (См. Рис. 14.4). Стационарный набор цен называется стационарной траекторией цен МС ДММФ, если её элементы удовлетворяют неравенствам (14.1.10), (14.1.12). Выполнение неравенства (14.1.11) не обязательно, т.е. стационарная траектория цен МС ДММФ может и не быть допустимой траекторией цен МС ДММФ.

Для стационарной траектории цен МС ДММФ имеем

или после сокращения на положительный множитель

(14.2.10)

Верно, очевидно, и обратное. Если основные характеристики и стационарного набора цен удовлетворяют векторному неравенству (14.2.10), то это набор есть стационарная траектория цен МС ДММФ.

Из всех стационарных траекторий цен МС ДММФ интерес представляют траектории с минимальным коэффициентом постоянного пропорционального падения цен в реальном времени (т.е. с минимальным коэффициентом постоянного пропорционального роста цен в обратном к реальному времени), т.е. траектория минимального постоянного пропорционального падения цен (ТрМиППРИ) в реальном времени.

Для определения этих траекторий следует решить задачу квадратичного программирования

(14.2.11)
(14.2.12)
(14.2.13)
(14.2.14)
(14.2.15)

Решение этой задачи представляет собой основные характеристики ТрМиППРИ Основные характеристики и определяются только матрицами и т.е. технологией ПС ДММФ.

Задача (14.2.11) – (14.2.15) эквивалентна следующей задаче на

(14.2.16)

в которой дроби вида и не рассматриваются.

Переход от задачи (14.2.11) – (14.2.15) к задаче (14.2.16) осуществляется с помощью следующих простых рассуждений.

Векторное неравенство (14.2.12) переписывается в координатной форме

(14.2.17)

Получается система неравенств с одной неизвестной Решение этой системы имеет вид

(14.2.18)

где дроби вида и не рассматриваются, ибо они соответствуют неравенствам которые удовлетворяются при любых значениях Для отыскания остаётся найти

Задачи вида (14.2.16) аналогичны задаче (14.2.7), они относятся к классу задач наглядной оптимизации и в общем виде трудно разрешимы. Однако при задачи вида (14.2.16) легко решаются на основании элементарных геометрических соображений. Проиллюстрируем это обстоятельство на двух примерах.

Пример 14.2.3. (продолжение примера 14.2.1)

Для матриц

имеем

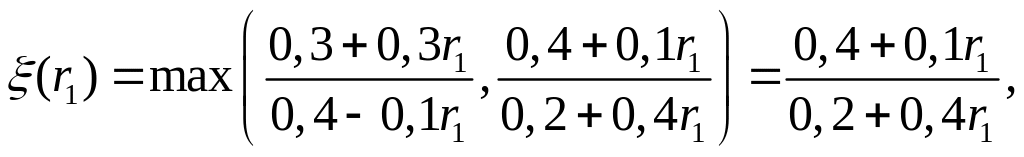Нарисуем эскизы графиков обеих дробно-линейных функций (I) и (II) (см. Рис. 14.5). Очевидно, графиком функции является линия ибо при а при Из элементарных геометрических соображений достигается при Для определения следует решить уравнение которое сводится к квадратичному уравнению корнями которого являются числа

Выбираем корень который попадает в отрезок второй корень является посторонним.

Осталось определить коэффициент падения

Таким образом задача на минимакс имеет решение

Пример 14.2.4. (продолжение примера 14.2.2)

Для матриц

имеем

Нарисуем графики обеих функций (I) и (II) (см. Рис. 14.6). Из элементарных геометрических соображений графиком функции является множество, состоящее из горизонтальной линии (без точки и изолированной точки Точка не рассматривается, ибо при правая дробь имеет вид и поэтому не учитывается. Самой низкой точкой этого множества является точка Следовательно, задача на минимакс имеет решение

Н епосредственно проверяется, что

Отметим, что в случае матриц и примеров 1 и 3 имеем В случае матриц и примеров 2 и 4