
- •I Понятие функции двух и более переменных, область определения функции
- •Примеры для самостоятельного решения
- •II Частные производные функции нескольких переменных
- •Примеры для самостоятельного решения
- •III Полный дифференциал функции нескольких переменных. Дифференциалы высших порядков
- •Примеры для самостоятельного решения
- •IV Производная по направлению и градиент
- •Примеры для самостоятельного решения
- •V Экстремум функций нескольких переменных
- •Примеры для самостоятельного решения
- •VI Условный экстремум
- •Задачи для самостоятельного решения
- •VII Наибольшее и наименьшее значения функции
- •Примеры для самостоятельного решения
- •Литература
Министерство образования Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
Ростовский Государственный Университет
Е.Р.Ляликова, Л.И.Спинко, С.В.Фоменко
Дифференциальное исчисление функций
нескольких переменных.
Методические указания для студентов 1-го курса
дневного отделения экономического факультета РГУ
Ростов-на-Дону 2004
Печатается в соответствии с решением кафедры математического анализа Ростовского государственного университета, протокол № 7 от 9 марта 2004 года.
Рецензент: доцент С.В.Фоменко
До сих пор мы рассматривали функции,
значения которых зависят от значений
одной переменной. При рассмотрении
многих вопросов естествознания приходится
иметь дело с такими зависимостями между
переменными величинами, в которых
числовые значения одной из них определяются
значениями нескольких других. Так,
например, площадь прямоугольника со
сторонами, длины которых равны
![]() и
и
![]() ,
определяется значениями двух переменных
и
,
а объем прямоугольного параллелепипеда
с ребрами
,
определяется значениями двух переменных
и
,
а объем прямоугольного параллелепипеда
с ребрами
![]() --
значениями трех переменных
.
Примеров таких зависимостей можно
привести много.
--
значениями трех переменных
.
Примеров таких зависимостей можно
привести много.
I Понятие функции двух и более переменных, область определения функции
Определение. Совокупность
упорядоченных пар действительных чисел
![]() называется двумерным координатным
пространством, где
-
первая координата,
-
вторая координата точки
называется двумерным координатным
пространством, где
-
первая координата,
-
вторая координата точки
![]() этого пространства.
этого пространства.
Если расстояние между двумя точками
![]() и
и
![]() определяется по формуле
определяется по формуле
![]() ,
то это двумерное пространство называется
евклидовым пространством и обозначается
,
то это двумерное пространство называется
евклидовым пространством и обозначается
![]() (вся
плоскость XOY). Аналогично
определяются трехмерное евклидово
пространство
(вся
плоскость XOY). Аналогично
определяются трехмерное евклидово
пространство
![]() ,
…,
,
…,
![]() -
n-мерное евклидово
пространство.
-
n-мерное евклидово
пространство.
Определение функции двух переменных.
Если каждой точке
множества
![]() по некоторому правилу
по некоторому правилу
![]() ставится в соответствие одно вполне
определенное действительное число
ставится в соответствие одно вполне
определенное действительное число
![]() ,
то говорят, что на множестве
,
то говорят, что на множестве
![]() определена числовая функция двух
переменных и пишут
определена числовая функция двух
переменных и пишут
![]() или
или
![]() .
Множество
называют областью определения функции
.
.
Множество
называют областью определения функции
.
Способы задания функции двух переменных, как и в случае одной переменной, могут быть различными. В примерах мы будем использовать аналитический способ задания, когда функция задается с помощью формулы. Областью определения функции в этом случае считается множество всех точек плоскости, для которых эта формула имеет смысл.
Рассмотрим примеры функций двух переменных.
1.
![]() .
Область определения этой функции –
множество
,
то есть вся плоскость XOY.
.
Область определения этой функции –
множество
,
то есть вся плоскость XOY.
2.
![]() .
Областью определения данной функции
является множество всех точек, для
которых выражение
.
Областью определения данной функции
является множество всех точек, для
которых выражение
![]() определено, то есть множество точек,
для которых
определено, то есть множество точек,
для которых
![]() ,
или
,
или
![]() .
Множество всех таких точек образует
.
Множество всех таких точек образует
круг с центром в начале координат и радиусом, равным единице.
3.
![]() .
Область определения этой функции –
множество точек, координаты которых
удовлетворяют неравенству
.
Область определения этой функции –
множество точек, координаты которых
удовлетворяют неравенству
![]() ,
то есть множество точек, лежащих вне
круга радиуса 1 и с центром в начале
координат.
,
то есть множество точек, лежащих вне
круга радиуса 1 и с центром в начале
координат.
Если вместо множества
точек плоскости взять множество точек
пространства, в котором каждая точка
имеет три координаты
,
то аналогично можно дать определение
функции трех переменных
![]() или
или
![]() .
Областью определения функции трех
переменных является все трех мерное
пространство или его часть. Аналогично
можно ввести понятие функций четырех
и вообще n
переменных
.
Областью определения функции трех
переменных является все трех мерное
пространство или его часть. Аналогично
можно ввести понятие функций четырех
и вообще n
переменных
![]() .
Однако области определения таких
функций уже не имеют наглядного
геометрического истолкования.
.
Однако области определения таких
функций уже не имеют наглядного
геометрического истолкования.
Заметим, что между функциями одной и функциями нескольких переменных имеются существенные различия. В то же время, переход от двух переменных к большему их числу, как правило, не представляет затруднений. Поэтому обычно мы будем подробно рассматривать только случай функций двух переменных.
Примеры для самостоятельного решения
Найти области определения следующих функций двух функций и изобразить их на плоскости:
1.
![]() ;
2.
;
2.
![]() ;
3.
;
3.
![]() ;
;
4.
![]() ;
5.
;
5.
![]() ;
6.
;
6.
![]() ;
;
7.
![]() .
.
II Частные производные функции нескольких переменных
Перенесем на функции нескольких переменных основные понятия дифференциального исчисления функций одной переменной, а, именно, понятия производной и дифференциала. Для функций нескольких переменных придется определять несколько производных, точнее, столько производных, сколько независимых переменных у данной функции.
Пусть функция
определена в некоторой окрестности
точки
.
Придадим переменной
приращение
![]() ,
а значение переменной
менять не будем, то есть перейдем на
плоскости от точки
к точке
,
а значение переменной
менять не будем, то есть перейдем на
плоскости от точки
к точке
![]() (
таково, что точка
(
таково, что точка
![]() принадлежит окрестности точки М). При
этом значение функции
принадлежит окрестности точки М). При
этом значение функции
![]() также изменится. Назовем это изменение
частным приращением функции
по переменной
:
также изменится. Назовем это изменение
частным приращением функции
по переменной
:
![]() .
.
Аналогично можно составить частное приращение по переменной :
![]() .
.
Определение. Если существует конечный предел
![]() ,
,
то он называется частной производной по переменной (по переменной ) от функции в точке .
Частные производные обозначаются одним
из следующих символов:
![]() ,
или
,
или
![]() ,
или
,
или
![]() ,
или
,
или
![]() .
Если нужно явно указать, в какой точке
вычислена частная производная, то пишут,
например, так:
.
Если нужно явно указать, в какой точке
вычислена частная производная, то пишут,
например, так:
![]() ,
или
,
или
![]() .
.
Из определения следует, что частная производная функции двух переменных равна обычной производной функции одной переменной, полученной при условии, что вторая независимая переменная сохраняет постоянное значение. Следовательно, правила и формулы отыскания частных производных те же, что и правила и формулы обычных производных функций одной переменной.
Найти частные производные следующих функций:
Пример
1.
![]() .
.
Функция
определена в области
![]() .
Фиксируя переменную
,
находим частную производную по переменной
:
.
Фиксируя переменную
,
находим частную производную по переменной
:
![]() .
.
Фиксируя переменную , получаем частную производную по переменной :
![]() .
.
Пример
2.
![]() .
.
Функция
определена при условии
![]() .
Фиксируя переменную
,
находим частную производную по переменной
:
.
Фиксируя переменную
,
находим частную производную по переменной
:
 .
.
Фиксируя переменную , получаем частную производную по переменной :
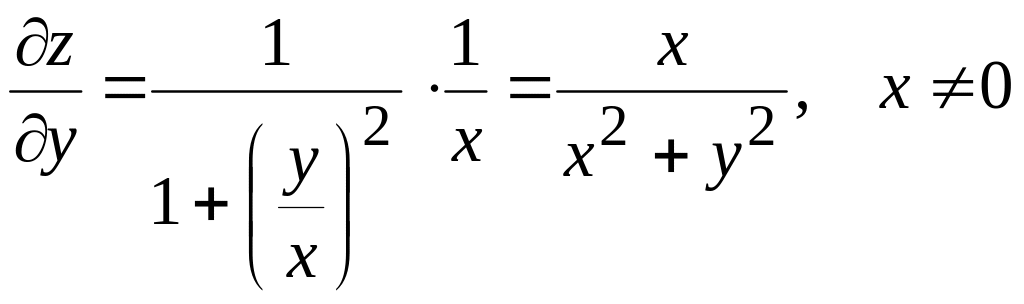 .
.
Пример
3.
![]() .
Доказать, что
.
Доказать, что
![]() .
.
Функция
определена при
![]() .
Найдем частные производные:
.
Найдем частные производные:
![]()
![]() .
.
![]() .
.
Проверим,
справедливо ли равенство, для этого
вычислим величину выражения
![]() ,
подставив туда найденные частные
производные:
,
подставив туда найденные частные
производные:
![]() ,
,
то есть действительно равенство верно.
Пример
4.
![]() .
Доказать, что
.
Доказать, что
![]() .
.
Функция определена при .
![]() .
Вычислим:
.
Вычислим:
![]() .
.
Следовательно, равенство верно.
Можно ввести понятие частной производной
порядка выше первого. Так как частные
производные
![]() и
и
![]() какой-либо функции двух переменных
какой-либо функции двух переменных
![]() сами являются, вообще говоря, функциями
двух переменных, то от них опять можно
брать частные производные по
и
.
Результат дифференцирования называется
частной производной второго порядка
(или просто второй частной производной).
Если от
взять частную производную по
,
то есть вычислить
сами являются, вообще говоря, функциями
двух переменных, то от них опять можно
брать частные производные по
и
.
Результат дифференцирования называется
частной производной второго порядка
(или просто второй частной производной).
Если от
взять частную производную по
,
то есть вычислить
![]() ,
то результат обозначается
,
то результат обозначается
![]() или
или
![]() .
От частной производной
можно взять частную производную по
:
.
От частной производной
можно взять частную производную по
:
![]() .
Результат дифференцирования называется
смешанной частной производной второго
порядка и обозначается:
.
Результат дифференцирования называется
смешанной частной производной второго
порядка и обозначается:
![]() или
или
![]() .
.
Таким же образом можно вычислить частные
производные второго порядка
![]() и
и
![]() ,
полученные от дифференцирования частной
производной
по
и по
соответственно.
,
полученные от дифференцирования частной
производной
по
и по
соответственно.
Справедливо утверждение: если смешанные
частные производные, отличающиеся
порядком дифференцирования, непрерывны,
то они не зависят от порядка
дифференцирования, то есть
![]() .
.
Пример
5. Найти частные производные второго
порядка функции
![]() .
.
Найдем частные производные первого порядка:
![]() ;
;
![]() .
.
Находим частные производные от этих:
![]() ;
;
![]()
![]() ;
;
![]() .
.
Так как смешанная производная второго порядка непрерывна на , то она не зависит от порядка дифференцирования, то есть .
Можно определить и производные более высоких порядков. Так для функции можно написать восемь частных производных третьего порядка:
![]() (или
(или
![]() ),
),
![]() ,
шестнадцать частных производных
четвертого порядка и так далее.
,
шестнадцать частных производных
четвертого порядка и так далее.
Если рассматривать функцию трех
переменных
![]() ,
то для нее имеем три частные производные
первого порядка
,
то для нее имеем три частные производные
первого порядка
![]() ,
девять частных производных второго
порядка
,
девять частных производных второго
порядка
![]() и так далее.
и так далее.
Заметим, что смешанные производные
любого порядка при условии их непрерывности
не зависят от порядка дифференцирования,
например
![]() .
.
