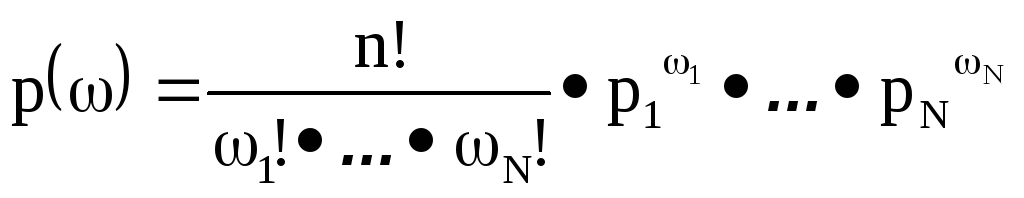Мультиномиальное распределение – схема бросания частиц по ячейкам

Пусть

• некоторые параметры (параметры распределения)

Воспользовавшись определением распределения и полиномиальной формулой, нетрудно проверить, что сумма вероятностей всех элементарных событий равна единице

Распределение на конечном пространстве, состоящем из целочисленных векторов называется мультиномиальное (полиномиальное) распределение, если

Указанное распределение возникает в следующей вероятностной схеме, называемой мультиномиальная (полиномиальная) схема или схема бросания частиц по ячейкам.

Рассмотрим последовательность из n независимых (с точки зрения здравого или физического смысла) опытов (бросание n частиц в N ячеек), в каждом из которых может произойти одно и только одно из событий A₁,…,A_N (A_i - попадание частицы в ячейку с номером i ). Пусть нам известна вероятность p_i , того что событие А_i произойдет в одном опыте (вероятность того, что частица попадет в i-тую ячейку) Поставим задачу найти распределение количества частиц в ячейках после n бросаний - мультиномиальное распределение.

Эта схема обобщает схему выбора с возвращением и схему Бернулли.

Элементарный исход, описывающий эксперимент целиком, естествено определить как n-мерный вектор, каждая координата которого может принимать одно из N значений 1,2,…,N.

Так же как и в схеме Бернулли определим вероятность элементарного исхода так, чтобы исходы отдельных опытов были независимы в совокупности. Дальнейшие рассуждения аналогичны рассуждениям, примененным при выводе формул в примере для схемы выбора с возвращением.

Геометрическое распределение – испытания до первого успеха

Пусть

Используя формулу для суммы членов бесконечной геометрической прогрессии покажите, что таким образом заданная функция является распределением

Распределение на пространстве натуральных чисел называется геометрическое распределение, если

Указанное распределение возникает в следующей вероятностной схеме, называемой схема испытаний до первого успеха.

Рассмотрим последовательность из независимых (с точки зрения здравого или физического смысла) опытов, в каждом из которых может произойти или не произойти некоторое событие A (“успех”). Пусть нам известна вероятность p , того что событие А произойдет в одном опыте. Вероятность того, что в первый раз событие A произойдет в k – том опыте дается формулой

Действительно , первые k-1 опытов должны закончиться неудачей (вероятность неудачи 1-p ), а последнее, к-тое, успехом (вероятность p).

Заметим , что в данном случае, мы не строим вероятностное пространство, полностью описывающее схему испытаний до первого успеха. Причиной этого является то, что в качестве пространства элементарных исходов в этом случае естественно, по аналогии со схемой Бернулли, рассмотреть множество бесконечных двоичных последовательностей (ведь неизвестно, когда наступит первый успех). Однако, это множество несчетно и задать на нем вероятность, оставаясь в рамках данной главы, невозможно.

Распределение Паскаля – испытания до m-того успеха

Покажите, что таким образом заданная функция является распределением

Распределение на пространстве натуральных чисел называется распределение Паскаля , если Здесь m – произвольное натуральное число.

Указанное распределение возникает в следующей вероятностной схеме, называемой схема испытаний до m-того успеха.

Рассмотрим последовательность из независимых (с точки зрения здравого или физического смысла) опытов, в каждом из которых может произойти или не произойти некоторое событие A (“успех”). Пусть нам известна вероятность p , того что событие А произойдет в одном опыте. Вероятность того, что в m – тый раз событие A произойдет в k – том опыте дается формулой

Действительно , в первых k-1 опытах должен быть ровно m-1 успех и в последнем, к-том, обязательно успех.