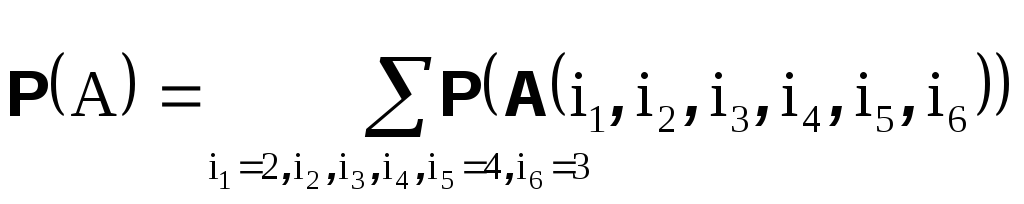Дискретная вероятностная модель
Вероятностное пространство называется дискретным, если его пространство элементарных исходов конечно или счетно.
В данном пункте мы переходим к описанию типовых математических моделей случайных событий. Начнем с простейшего случая.
Конечное пространство элементарных исходов
Пространство элементарных исходов называется конечным, если оно содержит конечное число элементарных исходов.
Классическая вероятностная модель
Классическая вероятностная модель
включает в себя
Конечное пространство элементарных исходов
Наибольшую сигма-алгебру (содержащую все подмножества пространства элементарных исходов).
Равномерную вероятностную меру, приписывающую равные вероятности всем элементарным исходам.
Из описания модели следует, что
Любое подмножество пространства элементарных исходов является событием
Любой элементарный исход имеет вероятность
|
Для того чтобы вероятность была конечно аддитивна |
Вероятность любого события можно определить как |
|
Априори – a priori, до опыта, т.е. с самого начала анализа до получения опытных данных. |
Применять эту модель следует в тех случаях, когда априори ясно, что все исходы опыта симметричны (равновероятны). |
Рассмотрим подробнее построение модели. Исходные данные для построения требуют, чтобы каждый элементарный исход имел одинаковую вероятность. Естественно потребовать, чтобы любое подмножество элементарных исходов было событием. Так как элементарные исходы образуют полную группу событий, то сумма их вероятностей должна быть равна 1, и из-за того, что все вероятности одинаковы, а количество элементарных исходов равно
имеем
Тогда для произвольного события A, используя конечную аддитивность вероятности получаем
|
Проверьте! |
Нетрудно проверить, что так определенная функция P будет вероятностью, и что требованиям модели удовлетворяет только одна такая функция. Следовательно, математическая модель определена однозначно. |
Связь классической вероятностной модели с комбинаторикой
Вычисления в классической модели сводятся к комбинаторной задаче определения количества элементов в множестве и его подмножествах. С другой стороны, если каким-либо иным образом узнать вероятность события в классической модели, то можно определить количество элементарных исходов в нем, т.е решить комбинаторную задачу методами теории вероятностей. Напомним некоторые формулы комбинаторики.
Основная формула комбинаторики
Пусть
и количество разных значений первой координаты равно n, а второй m. Тогда количество разных элементарных исходов равно m*n. Для доказательства достаточно представить все варианты в виде прямоугольной таблицы, строки которой пронумерованы значениями первой, а столбцы – второй координаты. Применяя индукцию можно распространить эту формулу на вектора с n координатами.
И этой формулы следует в частности, что количество всех двоичных векторов размерности n равно 2 n . И что количество всех подмножеств конечного множества с n элементами равно 2 n . И что количество различных вариантов выпадения очков на трех игральных костях равно 216. И т.д……
Факториал
Количество всех различных перестановок n различных чисел равно
Формула Стирлинга
Для приближенного вычисления факториалов больших чисел используется формула Стирлинга
Биномиальный коэффициент
Количество двоичных векторов размерности n с ровно k единицами равно
Бином Нютона
Полиномиальная формула
Схема выбора с возвращением
Частным случаем классической вероятностной модели является так называемая схема выбора с возвращением. Элементарный исход – это вектор
Схема является примером того, как можно строить сложные вероятностные модели из более простых. Эта схема применяется для описания ситуаций , в которых некоторый простой опыт с N возможными равновероятными исходами повторяется n раз.
Название схема получила от следующей ее интерпретации.
В урне находится N различных шаров. Из урны случайно вынимается один шар и записывается его номер
После этого шар возращается обратно в урну, и опыт поворяется снова (всего n раз).
Пример вычисления вероятности события в схеме выбора с возвращением.
Игральная кость бросается 20 раз. Найти вероятность того, что выпадет 2 единицы, 4 пятерки, 3 шестерки (событие A)
Решение.
В этом случае n=20, N=6.
|
Обратите внимание, что мы не ищем сразу вероятность исходного события, а придумываем как легче выразить это событие через другие, вероятность которых легче подсчитать |
Найдем вначале вероятность того, что в результате опыта выпадет i1 единиц, i2 двоек, i3 троек, i4 четверок, i5 пятерок, i6 шестерок (событие A(i1, i2 , i3 , i4, i5 , i6 )). Для этого необходимо подсчитать количество элементарных исходов, удовлетворяющих этому требованию. Используя формулы комбинаторики получаем, что искомое количество равно
Следовательно, вероятность равна
В нашем случае
Осталось сложить вероятности всех подходящих событий и найти вероятность A
Суммирование ведется по всем возможным значениям индексов, удовлетворяющих условиям. В частности, по i1=1, по i2 от 1 до 6, по i3 от 1 до 6 и т.д. |
|
Попробуйте вычислить эту вероятность. |
Вычисление этой вероятности не так то просто даже при наличии компьютера. Для этого придется написать небольшую программу. |
Схема выбора без возвращения
Схема выбора без возвращения отличается от предыдущей тем, что выбранный шар в урну не возвращается. Очевидно, что повторение опыта возможно лишь при n <=N. В этом случае
Соответствующий пример рассмотрим на семинаре.
Обе схемы являются частными случаями так называемой урновой схемы.