Неравенство Коши-Буняковского-Шварца. Ковариация

Доказательство. Если

то

и неравенство превращается в равенство.

Если

то, используя очевидное неравенство

получаем

что эквивалентно доказываемому неравенству.

Применяя неравенство КБШ к случайным величинам

получаем

Величина

называется ковариация случайных величин

и, как мы увидим в дальнейшем, является естественной мерой связи этих случайных величин между собой.

Величина

называется коэффициент корреляции случайных величин

Из неравенства КБШ следует, что

и если

то между этими случайными величинами существует (почти наверное) линейная зависимость

с положительным коэффициентом a. В этом случае говорят, что случайные величины положительно коррелированы. Если

то коэффициент a отрицателен и случайные величины отрицательно коррелированы. Коэффициент корреляции используют как меру зависимости случайных величин.

Неравенство Йенсена.Выпуклые функции

Функция f(x) называется выпуклой (как ), если

Например, функции , exp(x) выпуклы.

Для выпуклых функций справедливо неравенство Йенсена

Доказательство следует из определения выпуклой функции, если в нем положить

и воспользоваться свойствами 1) 2) 3) математического ожидания.

Моменты

Величина

называется к-тый момент (к-тый начальный момент) случайной величины.

Величина

называется к-тый абсолютный момент случайной величины.

Величина

называется к-тый центральный момент случайной величины.

Ясно, что математическое ожидание это первый момент, а дисперсия второй центральный момент. Моменты часто используются в качестве дополнительных характеристик случайных величин.

Вычисление математического ожидания.

Если случайная величина простая, то ее математическое ожидание вычисляется непосредственно по определению. Например, если все значения

случайной величины

равновероятны, то ее математическое ожидание равно среднему арифметическому этих значений

Заметим , что у простой случайной величины математическое ожидание всегда конечно.

Для дискретной случайной величины, принимающей счетное число различных значений, имеем (приближая ее снизу последовательностью простых случайных величин)

Этот ряд не всегда сходится, и поэтому существуют дискретные случайные величины, не имеющие конечного математического ожидания. Простым достаточным условием конечности математического ожидания является ограниченность модуля случайной величины сверху (константой или другой случайной величиной, имеющей конечное математическое ожидание).

Заметим, что для вычисления математического ожидания дискретной случайной величины нам достаточно знать только ее распределение. Этот факт справедлив и в общем случае, что показывает следующая теорема.

Теорема Лебега о замене переменных

Пусть

случайная величина и g(x) – борелевская функция

Тогда

если хотя бы один из этих интегралов существует.

Вычисление интеграла Лебега на прямой.

Так как на распределение на прямой однозначно определяется функцией распределения

то интеграл Лебега часто обозначают так

и называют интегралом Лебега-Стильтьеса от функции g по функции F.

Если функция распределения имеет плотность

то предыдущий интеграл интеграл превращается в интеграл

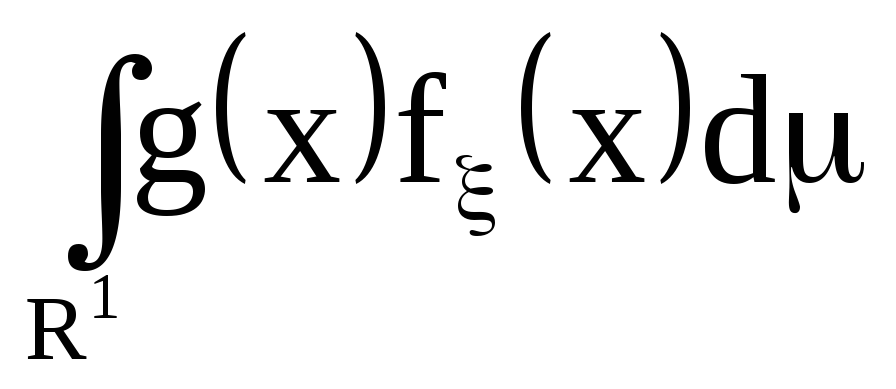
где

мера Лебега на прямой.

Можно показать, что

если функция g (x) интегрируема по Риману, то

где последний интеграл понимается в смысле Римана.

Таким образом, в практически важных случаях вычисление интеграла Лебега сводится к вычислению конечной суммы, ряда или интеграла Римана (или их комбинаций). В дальнейшем для интегралов по мере Лебега будем опускать символ и использовать такое же обозначение как и для интегралов Римана.