Смеси распределений.
Пусть
конечный или счетный набор распределений на одном и том же измеримом пространстве и
дискретное распределение, т.е.
Тогда функция
так же будет распределением, которое называется смесь распределений
Числа
называются коэффициентами смеси.
Ситуацию, в которой возникает смесь распределений, можно представить себе, например, так. Случайно, в соответствии с распределением
выбирается одна из вероятностей
а затем проводится эксперимент в соответствии с выбранной вероятностью.
При смешивании распределений, очевидно, аналогичным образом смешиваются их функции распределения и (если существуют) плотности. Смешаем два бета-распределения B(2,6) и B(6,2) с коэффициентами 1/2. График плотности получившегося распределения приведен на рисунке
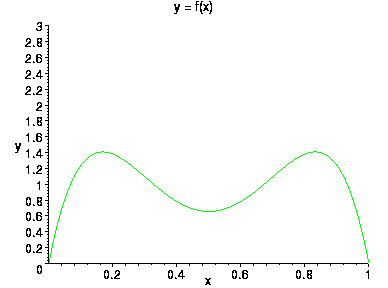
Данную плотность можно использовать для моделирования стрельбы по одной мишени двух стрелков, один из которых целится в точку
а другой – в точку
Смешивая различные бета-распределения, можно моделировать различые способы выбора случайной точки на отрезке. На следующем рисунке приведен график плотности смеси пяти бета-распределений.
Нормальное (гауссовское) распределение.
Рассмотрим положительную функцию
|
Докажите
это, переходя к полярным координатам
в интеграле |
Так как
то функция |
,
который , очевидно, равен квадрату
исходного.
является плотностью и задает так называемое стандартное нормальное (гауссовское) распределение.
График этой плотности приведен на рисунке
Общее нормальное распределение задается плотностью
где
параметры распределения.
|
Покажите,
что если |
Нормальное распределение обладает большим количеством замечательных свойств, многие из которых мы рассмотрим в дальнейшем. Это распределение использовал Гаусс в модели случайных ошибок измерения. Случайная величина, имеющая нормальное распределение, называется нормальная или гауссовская случайная величина. Для этого распределения используют обозначение |
,то
.
Графики плотности
Экспоненциальное (показательное) распределение.
Рассмотрим плотность
где
параметр распределения. Распределение с такой плотностью называется экспоненциальное или показательное распределение. Приведем график плотности этого распределения при
|
Для доказательства достаточно воспользоваться формулой условной вероятности. Можно показать, что экспоненциальное распределение это единственное распределение, из распределений имеющих плотность, с таким свойством. |
Экспоненциальное распределение применяется при моделировании различных временных интервалов - времени жизни технических устройств, интервалов между моментами регистрации радиоактивных частиц датчиками радиации, интервалов между последовательными звонками в телефонной сети и т.п. Это распределение обладает замечательным свойством, которое называется отсутствие последействия. Именно, если
имеет экспоненциальное распределение, то
|
|
Покажите,
что, если |
С точки зрения теории надежности это распределение описывает нестареющий элемент, т.е. в любой момент времени элемент имеет то же распределение остаточного времени жизни, что и новый элемент. Случайная величина, имеющая такое распределение называется экспоненциальная или показательная случайная величина. Это распределение обозначается |
,то
