Марковская зависимость

Легко распространить изложенное выше на случай элементарного исхода с n целочисленными координатами.

Особенно просто записывается вероятность элементарного исхода когда имеет место марковская зависимость координат, т.е. когда распределение следующей координаты зависит только от значения предыдущей координаты

В этом случае последовательные переходы от координаты к координатеи т.д. называются шагами ,а вероятности

называются переходными вероятностями (за один шаг).

Если каждая координата вектора принимает значения в одном и том же конечном множестве(множестве состояний) и переходные вероятности не зависят отn, то последовательность называется конечной цепью Маркова. В этом случае вероятность элементарного исхода можно записать так

где

- количество переходов из состояния i в состояние j

Подробно марковские зависимости исследуются в теории случайных процессов.

Формула полной вероятности и формула Байеса

Часто при решении простых задач теории вероятностей формально не вводят вероятностное пространство, а сразу выделяют полную группу случайных событий (условий), вероятности которых легко определить из условий задачи и вероятность интересующего события находят по формуле полной вероятности

Например, рассмотрим следующую задачу.

В ящике содержатся детали, поступившие с трех разных заводов.

Доля брака среди деталей первого завода – 0,1, второго - 0,2, третьего - 0,4.

Количество деталей первого завода в ящике - 20, второго –30, третьего – 50. Найти вероятность того, что наудачу выбранная из ящика деталь окажется бракованной (событие A).

Решение. При формальном определении, в качестве элементарного исхода следует взять вектор с двумя координатами. Первая указывет номер завода, с которого поступила наудачу выбранная деталь, вторая - бракована эта деталь или нет. Далее действуя в духе предыдущего пункта легко определить вероятности всех элементарных исходов и соответственно, вероятность любого события A по формуле

С другой стороны обозначив B₁, B₂, B_{3 –} события, заключающиеся в том, что деталь поступила, соотвественно, с первого, второго, третьего завода, и применив формулу полной вероятности, получим

Различие в двух подходах к решению данной задачи состоит в том , что в первом случае полностью определяется вероятностное пространство и можно найти вероятность любого события по одной и той же формуле, во втором модель полностью не строится и мы (по существу) определяем вероятности только тех элементарных исходов, которые входят в интересующее нас событие.

С формулой полной вероятности тесно связана формула Байеса.

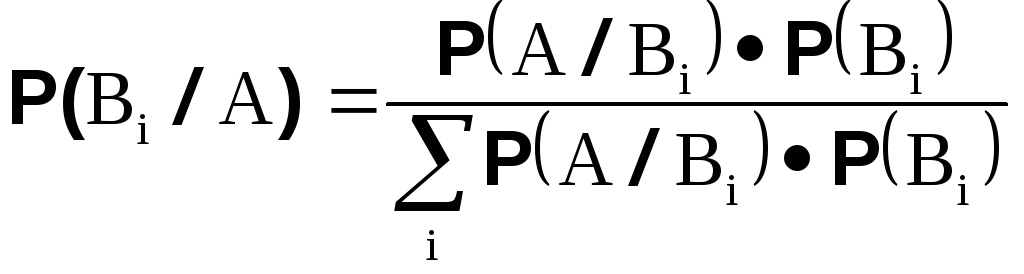
Она позволяет найти, как, иногда, говорят инженеры, обратные вероятности, т. е. вероятности событий полной группы при условии, что произошло событие A.

Например, пусть в условиях предыдущей задачи известо, что из ящика извлечена бракованная деталь и требуется найти вероятность того, что она выпущена вторым заводом. Тогда по формуле Байеса имеем

Заметим, однако принципиальную разницу этих формул. Формула полной вероятности является просто следствием свойства счетной аддитивности вероятности и ее применение часто означает, что мы неявно строим вероятностное пространство. Формула Байеса действительно расчетная – для ее применения требуется , чтобы вероятностное пространство уже было определено.