Решить задачи

Задача № 15.1

Выяснить, для каких из нижеприводимых функциональных связей удовлетворяются условия аддитивности и однородности?

1) у = ах 2) у = аsinх.

Задача № 15.2

На нелинейный конденсатор с характеристикой С=С₀(1-qu) подается линейно растущее напряжение u = bt.

Найти закон изменения тока через конденсатор.

Ответ: i_c=bC₀(1-2qbt).

Задача № 15.3

Нелинейное сопротивление и резистор R = 1000 Ом соединены последовательно. Напряжение источника напряжения U = 5 В. определить ток в цепи и величины напряжений на нелинейном элементе и резисторе. Вольтамперная характеристика нелинейного элемента приведена на рис.15.1 (кривая 1).

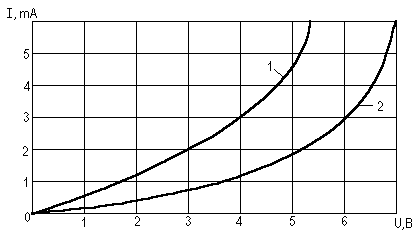
Рис.15.1

Задача № 15.4

Электрическая цепь с двумя нелинейными сопротивлениями показана на рис.15.2, нелинейное сопротивление R₂ имеет вольтамперную характеристику 1 (рис.15.1). Нелинейное сопротивление R₃ обладает вольтамперной характеристикой 2 (рис.15.1). Сопротивление R₁=1000 Ом, Е=6 В. определить ток через резистор R₁.

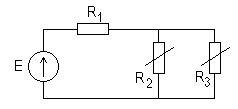
Рис. 15.2

Задача № 15.5

К нелинейному сопротивлению, характеристика которого аппроксимальна ломанной прямой (U_н= -2 В, S= 1мА/В), приложено напряжение u= -10+16 cos_оt В. найти постоянную составляющую и первую гармонику тока.

Ответ: I_о=1,73 А, I₁=3.14 А.

Примеры решения задач

Задача № 15.6

Выяснить, удовлетворяется ли принцип суперпозиции для выражения y=ax², у=acosx ?

Решение

Исходя из принципа суперпозиции

F(x₁+x₂)=f(x₁)+ f(x₂)

для функциональной зависимости у=ах², будем иметь, что у₁=а(х₁+х₂)², у₂=ах₁+ах₂.

Так как , то принцип суперпозиции не выполняется.

Для зависимости у = acosx найдем, что

у₃ = ассоs(х₁+х₂) и у₄ = асоsх₁+аcosх₂.

Так как , то принцип суперпозиции также не выполняется.

Следовательно, эти зависимости не принадлежат линейной цепи, для которой верен принцип суперпозиции, а принадлежат нелинейной цепи.

Задача № 15.7

Индуктивность катушки меняется во времени по закону

L(t)=L₀(1+mcost).

Найти напряжение на этой катушке, если через нее пропускается ток высокой частоты i(t)=I₀sint и убедиться в том, что напряжение не повторяет форму тока.

Решение

Для определения напряжения на катушке воспользуемся компонентным уравнением для индуктивности

Исходя из этого, определим, что

Задача № 15.8

По нижеприведенным выражениям вольтамперных характеристик найти зависимость для дифференциального сопротивления и дифференциальной проводимости:

Решение

Для определения дифференциального сопротивления и дифференциальной проводимости воспользуемся формулами

Для соответствующих вольтамперных характеристик получим:

Задача № 15.9

К нелинейному сопротивлению, характеристика которого аппроксимирована ломаной прямой (U_н= -20B, S=4A/B), приложено напряжение u=U₀+20cos₀t B.

Определить, при каком смещении U₀ амплитуда второй гармоники тока максимальна и вычислить ее значение.

Решение

Из зависимостей Берга известно, что амплитуда второй гармоники максимальна при угле отсечки =60⁰.

Используя формулу найдем, что

Для определения амплитуды второй гармоники предварительно вычислим величину I_m по формуле

и далее найдем, что

Задача № 15.10

На вход нелинейного элемента с характеристикой i=f(u_вх) аппроксимированной степенным рядом, подается напряжение

U_вх=U₀+U_mcos₀t=-3+2cos₀t B.

Уравнение характеристики задано выражением

i=b₀+b₁u_вх+b₂u_вх² ,

где b₀=5мА, b₁=2 мА/В, b₂=0.2 мА/В².

Найти нулевую составляющую, амплитуды первой и второй гармоник выходного тока нелинейного элемента.

Решение

Находим коэффициенты разложения в ряд Тейлора

Определим постоянную составляющую и амплитуды первой и второй гармоник:

Библиографический список

1. Гоноровский И.С. Радиотехнические цепи и сигналы: Учебник для вузов. 4-е изд., перераб. и доп. М.: Радио и связь, 1986. 512 с.

2. Основы теории цепей: Учебник для вузов/ Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. 5-е изд., перераб. М.: Энергоатомиздат, 1989. 528 с.

3. Попов В.П. Основы теории цепей: Учебник для вузов. М.: Высш. шк., 1985. 496 с.

ЛР № 066815 от 25.08.99. Подписано к печати

Формат 60х84/16. Бумага для множительных аппаратов.

Усл.п.л. 1,6 Уч.- изд.л. 1,5 Тираж 100 экз.<<C>> 34

Зак.№

Воронежский государственный технический университет

394026 Воронеж, Московский просп.,14

8