МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Воронежский государственный технический университет

Радиотехнический факультет

Кафедра радиотехники

МЕТОДИЧЕСКОЕ РУКОВОДСТВО

к самостоятельной работе по занятиям № 13,14,15 курса

“Общая электротехника и электроника” для сту-

дентов специальности 210201 “Проектирование

и технология радиоэлектронных средств” дневной

и заочной форм обучения

Воронеж 2004

Составитель канд.техн.наук ,доц. Б.В. Матвеев

УДК 621.396

Методическое руководство к самостоятельной работе по занятиям №13,14,15 курса “Общая электротехника и электроника” для студентов специальности 210201 “Проектирование и технология радиоэлектронных средств” дневной и заочной форм обучения/Воронеж.гос.тех.ун-т; Сост.Б.В. Матвеев. Воронеж, 2004. 21 с.

В работе приведены методические указания к самостоятельной работе по темам: “Спектры”, длинная линия, нелинейные цепи”. Приводятся краткие теоретические сведения и необходимые формулы для выполнения домашнего задания. Даны наиболее характерные примеры решения задач, обеспечивающие лучшее усвоение материала студентами. Предназначено для студентов второго курса.

Ил. 12. Библиогр.: 3 назв.

Рецензент канд. техн. наук В.П.Литвиненко

Ответственный за выпуск зав.каф.РТ проф. Г.В.Макаров

Печатается по решению редакционно–издательского совета Воронежского государственного технического университета.

 Воронежский государственный технический университет, 2004

Занятие № 13

СПЕКТРЫ

Литература

[1, c. 17-54], [2, c. 200-208], конспект лекций.

Домашнее задание

Подготовиться к ответам на вопросы по следующим разделам:

1. Базисные функции. Ортогональная и ортонормированная системы функций. Спектр Фурье.

2. Спектр периодического сигнала. Тригонометрическая и комплексная формы разложения периодического сигнала в ряд Фурье.

3. Спектр непериодического сигнала. Прямое и обратное преобразования Фурье.

4. Зависимость между параметрами периодического сигнала и его спектром. Ширина спектра. Распределение мощности в спектре периодического сигнала. Равенство Парсеваля.

5. Распределение энергии в спектре непериодического сигнала.

Решить задачи

Задача № 13.1

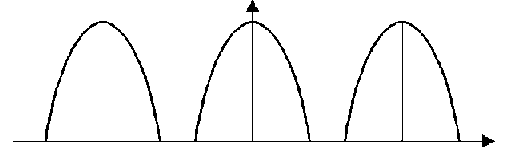
Разложить в тригонометрический ряд Фурье периодическую функцию (рис. 1), получаемую при однополупериодном "выпрямлении" косинусоиды s(t)=cost при -/2t/2

0 2π

Рис. 13.1

Ответ:

Задача 13.2

Используя комплексную форму разложения периодического сигнала в ряд Фурье, определить спектр сигнала (рис. 13.2), задаваемый аналитическим выражением

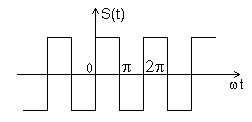
Рис.13.2

Ответ:

Задача № 13.3

Определить спектральную функцию импульса (рис. 13.3), который задается следующим выражением

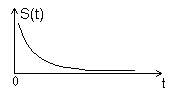
Рис.13.3

Ответ:

,

Примеры решения задач Задача 13.4

Разложить в тригонометрический ряд Фурье знакопеременную прямоугольную функцию (рис.13.4), определяемую выражением

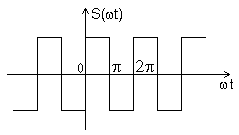
Рис.13.4

Решение

Обозначим через  величину t, т. е. t= и запишем выражение для спектра функции в виде

Ввиду того, что функция s() симметрична относительно горизонтальной оси, то в спектре будет отсутствовать постоянная составляющая, т. е. а₀/2=0.

С учетом несимметричности s() относительно вертикальной оси получаем, что а_n=0, т. е. в спектре сигнала не будет косинусоидальных составляющих.

Определим коэффициент b_n, используя формулу

Учитывая значения, принимаемые функцией S(), находим что

Придавая n значения 1,2,3 и т.д., получаем, что

Таким образом функция S() будет иметь следующий спектр:

.

Задача № 13.5

Используя комплексную форму разложения периодического сигнала в ряд Фурье, определить спектр сигнала (рис.13.5), определяемый выражением

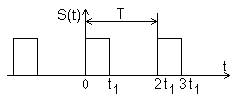
Рис.13.5

Решение

Определяем комплексную амплитуду сигнала S(t) с учетом, что T=2t₁, как

Принимая во внимание, что , получаем. что

Используя выражение е^-jn=cos n-j sin n и принимая во внимание, что sin n=0 для n=1,2,3,…,получим, что для нечетных n

Комплексный ряд Фурье для сигнала будет иметь вид

В тригонометрической форме спектр сигнала записывается как

Постоянная составляющая сигнала определяется по формуле, с учетом, что n=0

Составляющие спектра сигнала определяется как

При n=1, 3, 5, 7, … получим, что

Задача № 13.6

Определить спектральную функцию одиночного прямоугольного импульса (рис. 13.6)

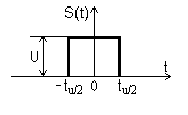
Рис.13.6

Построить график спектральной функции.

Решение

Для определения спектральной функции воспользуемся формулой

С учетом того, что импульс симметричен относительно вертикальной оси, получим, что

Умножив и разделив полученное выражение на j2, применив формулу Эйлера для sin , найдем, что

После преобразования этого выражения получим, что