2.2 Тест Колмогорова – Смирнова.

Объективная проверка на нормальное распределение проводится с помощью подходящего статистического критерия (теста Колмогорова-Смирнова). При помощи этого теста по выбору можно проверить, соответствует ли реальное распределение переменной нормальному, равномерному, экспоненциальному распределению или распределению Пуассона. Разумеется, самым распространённым видом проверки является проверка наличия нормального распределения.

Выберите в меню Analyze(Анализ) NonparametricTests (Непараметрические тесты) 1-Sample KS (К-С одной выборки).П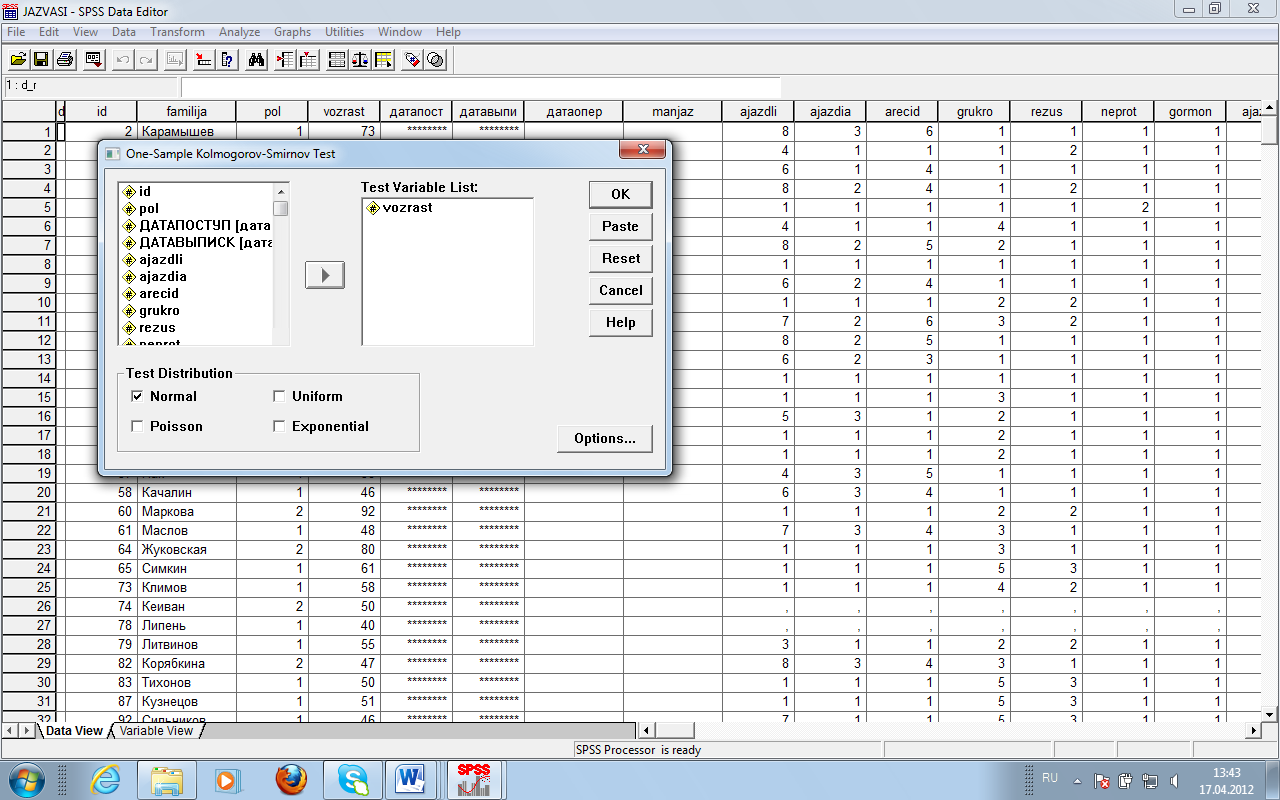 оявится диалоговое окно OneSampleКolomgorov-SmirnovTest (Тест Колмогорова-Смирнова для одной выборки) (см. рис.). Вводим переменную vozrast и нажимаем ОК.

В результате получаем таблицу с анализом на предмет соответствия переменной vozrast нормальному закону.

Расшифровка таблицы ОneSampleКolomgorov-SmirnovTest

		возраст
N		582
NormalParameters (Параметр нормального распределения) а' ь	Mean (Среднее значение) Std. Deviation (Стандартное отклонение)	48,82 15,31
Most Extreme Differences (Экстремальные разности)	Absolute (Абсолютные) Positive (Положительные) Negative (Отрицательные)	,057 ,057 -,029
Z Колмогорова-Смирнова		1,373
Asymp. Sig. (2-tailed) (Статистическая значимость (2-сторонняя))		,046

a. Test distribution is Normal. (Тестируемое распределение является нормальным распределением.) 

b. Calculatedfromdata. (Рассчитано исходя из исходных данных.)

Полученные результаты включают:

•  среднее значение и стандартное отклонение

•  промежуточные результаты, полученные в результате теста Колмогорова-Смирнова

•  вероятность ошибки р.

Отклонение от нормального распределения считается существенным при значении

р< 0,05; в этом случае для соответствующих переменных следует применять непараметрические тесты. В рассматриваемом примере ( значение р = 0,046), то есть вероятность ошибки является не значимой; поэтому значения переменной достаточно хорошо подчиняются нормальному распределению.

Провести исследование 2-3 переменных (bolidlit и rvotdlit) с использованием Колокола Гаусса и теста Колмогорова-Смирнова на предмет их соответствия нормальному распределению. Результаты исследования переменных с их графиками и таблицами представить в отчете.

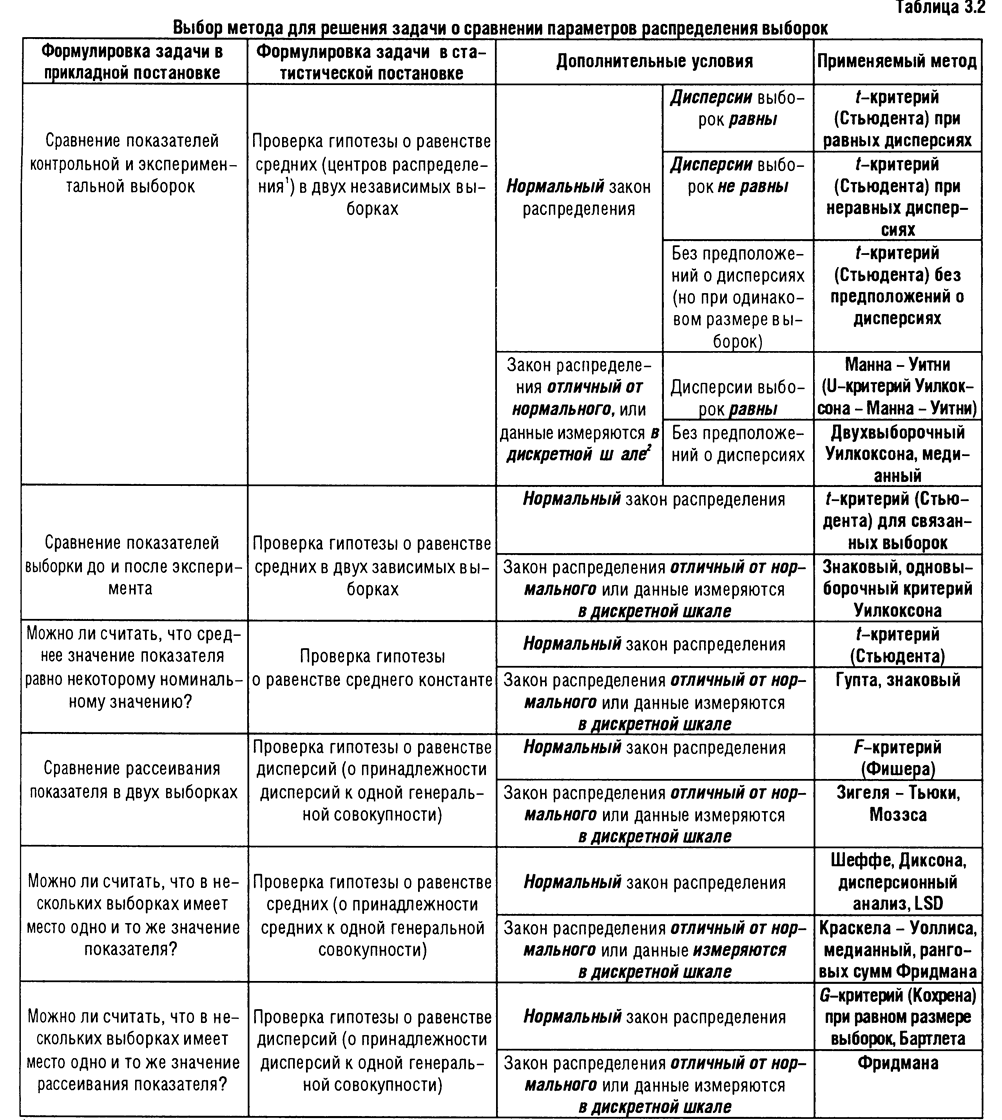
Необходимость исследование на нормальность распределения обусловлена прежде всего тем, что существуют различные подходы к решению статистических задач в зависимости от того под какой закон распределения мы можем подвести ту или иную случайную величину. В таблице 3.2 приведены примеры задач по статистической обработке данных имеющих различные функции распределения и соответственно свои способы решения задач.