1.3. Резистивные элементы.

Одним из приёмников электрической цепи является резистивный элемент - резистор. В резистивном элементе электромагнитная энергия преобразуется в тепло в соответствии с законом Джоуля – Ленца Q = I²Rt. Параметром, характеризующим резистор, является активное сопротивление R, измеряемое в омах (Ом). Резистивные (или их ещё называют активные) сопротивления вводятся в схемы замещения элементов цепи для учета необратимого преобразования электромагнитной энергии в другие виды (например, тепловую, механическую, энергию излучения и т. п.).

Для расчета токов и напряжений в цепи необходимо задать положительные направления токов и напряжений в элементах цепи. За положительное направлением тока и напряжения выбрано их направление от узла с большим потенциалом к узлу с меньшим потенциалом (рис. 1.4)

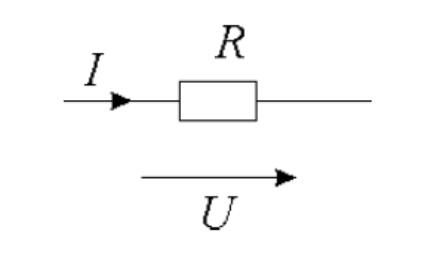
Рис. 1.4

В резистивном элементе напряжение связано с током законом Ома:

U= IR, (1.4)

где R – электрическое сопротивление проводника; U – падение напряжения на участке цепи; I – ток в цепи.

В электротехнике разность потенциалов на концах сопротивления называют либо напряжением на сопротивлении, либо падением напряжения на сопротивлении.

Положительное направление падения напряжения, указываемое на рисунках стрелкой, совпадает с положительным направлением тока, протекающему по данному сопротивлению.

Для участка цепи, не содержащего ЭДС, связь между током и напряжением указывается законом Ома. Применительно к схеме рис.1.4:

U_ab = IR, (1.5)

. (1.6)

Рассмотрим участок электрической цепи, содержащей не только сопротивление, но и ЭДС (рис.1.5).

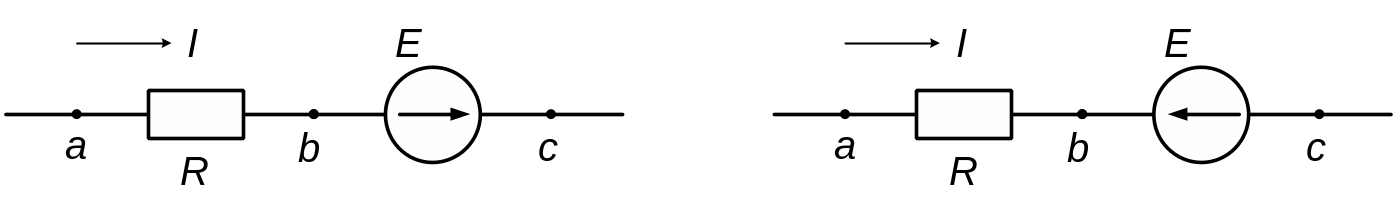
а) б)

Рис.1.5

Найдем разность потенциалов (напряжение) между точками “a” и “c” для этих участков. По определению,

U_ac = φ_a – φ_c. (1.7)

Выразим потенциал точки “a” через потенциал точки “c”. При перемещении от точки “c” к точке “b” встречно направлению ЭДС E (рис.1.5а) потенциал точки “b” оказывается ниже (меньше), чем потенциал точки “c” на величину ЭДС E:

φ_b = φ_c – E. (1.8)

При перемещении от “c” к точке “b” согласно направлению ЭДС E (рис.1.5б) потенциал точки “b” оказывается выше (больше), чем потенциал точки “c” на величину ЭДС E:

φ_b = φ_c + E. (1.9)

Так как ток течет от более высокого потенциала к более низкому, в обеих схемах (рис.1.5) потенциал точки “a” выше потенциала точки “b” на величину падения напряжения на сопротивлении R:

φ_a = φ_b + IR. (1.10)

Таким образом, для рис.5а:

φ_a = φ_c – E + IR (1.11)

или U_ac = φ_a - φ_c = IR – E , (1.12)

а для рис.1.5б:

φ_a = φ_c + E + IR (1.13)

или U_ac = φ_a - φ_c = IR + E. (1.14)

1.4. Закон Ома для ветви с источниками эдс

Для получения закона Ома для ветви с источниками ЭДС (рис. 1.6) воспользуемся вторым законом Кирхгофа, составленным для контура, образованного этой ветвью и напряжением между узлами, к которым она присоединена

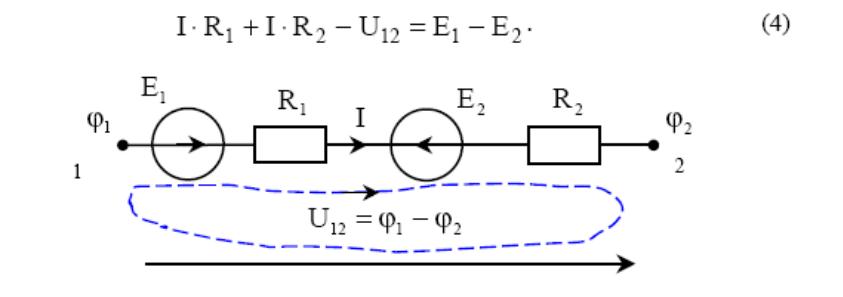
Рис. 1.6

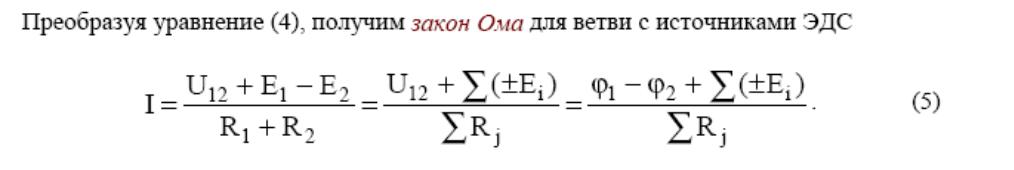
При определении тока I положительное направление напряжения U₁₂ необходимо выбрать по току I, а знак у ЭДС +Ei , если ток и ЭДС совпадают по направлению, и - Ei , если не совпадают.

Если значение сопротивления резистора не зависит от тока, протекающего через него, то такой резистор называется линейным, а электрическая цепь, состоящая только из таких резисторов, - линейной резистивной. Вольт амперная характеристика (ВАХ) такого элемента представляет собой линейную функцию, проходящую через начало координат.