- 15 -

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МАТИ» - РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ

УНИВЕРСТИТЕТ им. К.Э.ЦИОЛКОВСКОГО

Кафедра «Информационные технологии»

Лабораторные работы

по дисциплине

"Вычислительная математика"

Курс третий

Семестр пятый

Составил к.т.н., доцент Калинин Б.Н.

Москва – 2012 г

Cодержание

1. Вводная работа 3

Основные вопросы 3

2. Решение уравнений 6

Теоретические сведения 6

Варианты заданий 9

3. Решение систем линейных алгебраических уравнений 11

Теоретические сведения 11

Варианты заданий 14

1. Вводная работа по овладению основными навыками работы в системе Mathematica

Задание: В среде Mathematica напечатать приведенный ниже текст, запустить на счет и разобраться в полученных результатах.

Для получения зачета нужно уметь объяснить, как выполняется каждая команда. Описание команд содержится в Краткой инструкции пользователя пакета прикладных программ Mathematica.

Заголовок работы: “Лабораторная работа студента группы №, Ф. И.”.

Замечание 1. Комментарии выделяются скобкам и звездочками: (*…*). Для того, чтобы сделать комментариями всю выделенную ячейку, достаточно нажать на клавиши Alt+n, где n=1,…,7.

Замечание 2. Все вводимые выражения автоматически помещаются в ячейки. Отсутствие разделительного знака между выражениями означает, что эти выражения должны быть помещены в разные ячейки. Следовательно, перед вводом второго из пары таких выражений нужно открыть новую ячейку.

Основные вопросы

1. Основные части пакета Математика.

2. Точные и приближенные вычисления.

3. Операции с ячейками: объединение и разделение ячеек, группирование ячеек. Скрытие содержания группы ячеек.

4. Правила написания. Малые и большие буквы. Запись операции умножения. Употребление скобок.

5. Наиболее часто употребляемые операции и функции. Тригонометрические функции. Экспоненциальная функция и логарифм. Вычисление пределов. Вычисление производных. Численное и аналитическое интегрирование. Нахождение минимумов и максимумов. Циклические операции суммирования и умножения. Функция Fit. Функция Print. Получение информации о функциях.

6. Стандартная, префиксная и постфиксная формы обращения к функциям.

7. Циклические операции: For, While и Do. Логические операторы. Функция If.

8. Функции пользователя. Операции немедленного и задержанного присваивания. Шаблоны для описания типов аргументов.

9. Простейшие программы. Конструкция Module.

10. Понятие списка. Простой способ определения списка. Функции Range и Table. Операции с элементами списков. Определение векторной функции. Матричные функции.

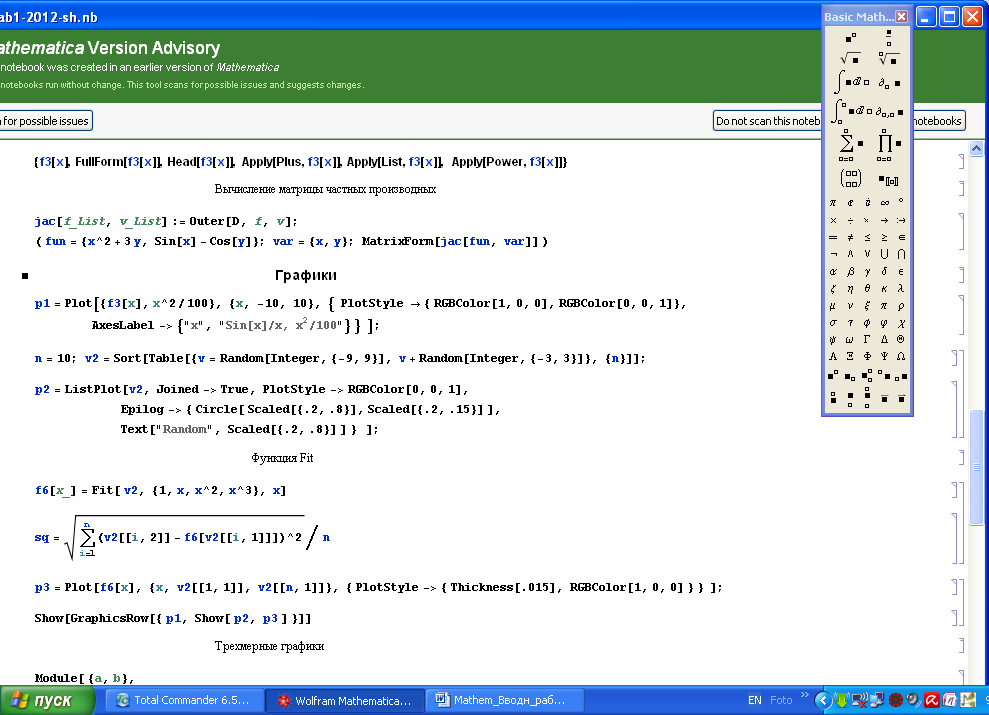
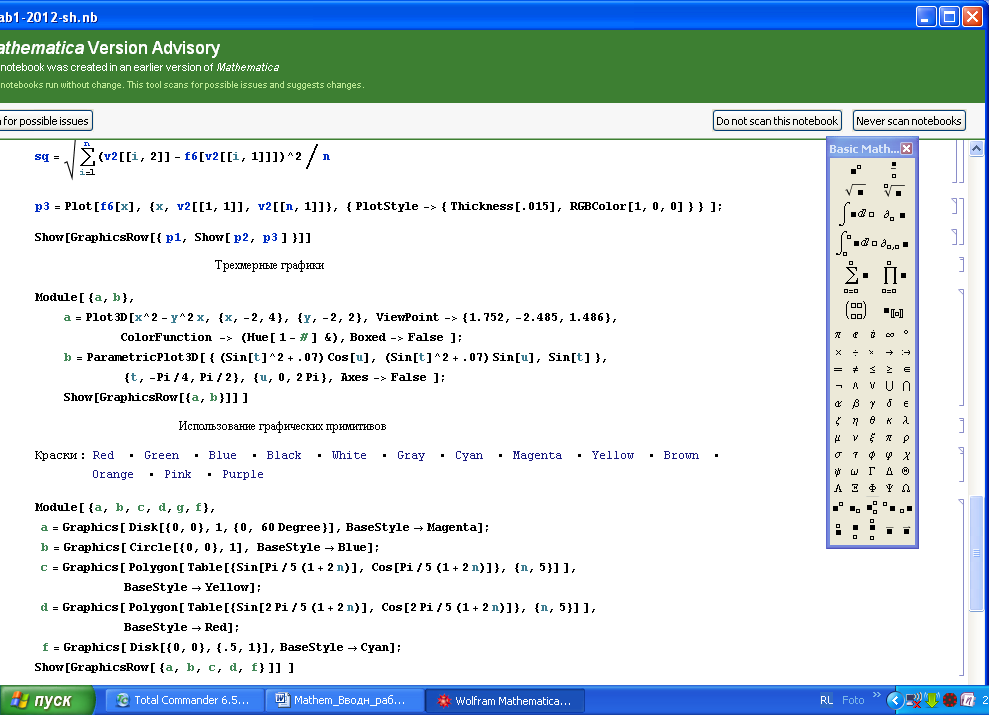
11. Графики. Создание двумерного графика Plot. Основные опции графиков. Установление одинакового масштаба по осям координат. Другие типы графиков: ListPlot, параметрические графики, трехмерные графики. Функция Show. Массив графиков.

12. Решение уравнений. Функции: Solve, LinearSolve, Roots, FindRoot.

13. Преобразование выражений. Представление выражений в форме FullForm. Операции с элементами выражений. Операции с заголовками выражений.

14. Оператор Outer.

2. Решение уравнений

Найти решение уравнения с точностью следующими методами:

- дихотомии,

- пропорциональных частей (хорд),

- касательных (Ньютона),

- модифицированным методом Ньютона,

- комбинированным методом,

- итерационным, -

предварительно отделив корни.

Сравнить скорость сходимости методов.

Сравнить полученные результаты с результатами, вычисленными с помощью встроенных функций пакета Математика.

Для получения зачета студент должен продемонстрировать на экране компьютера действующую программу, реализующую перечисленные выше методы решения. Студент должен обосновать выбор отрезка для поиска решения уравнения, а также должен уметь объяснить все детали представленной программы и ответить на связанные с темой теоретические вопросы.