Раздел 3. Основы математического анализа

Тема 3.6. Теория рядов Задание 41. Нахождение радиуса и интервала сходимости степенного ряда – 1 ч.

Цель: формирование умения находить радиус и интервал сходимости степенных рядов.

Задание для самостоятельной внеаудиторной работы:

 41.1. Выучите определение степенного ряда. Сформулируйте определение радиуса сходимости степенного ряда. Выясните, какова техника его нахождения.

 41.2. Проанализируйте, в каких случаях для вычисления радиуса сходимости степенного ряда l удобно искать по формуле l= , а в каких – по формуле – l= . Внимательно изучите примеры, позволяющие находить радиус сходимости степенного ряда.

41.3. Найдите радиус сходимости степенного ряда:

а) ; б) ; в) ;

г) ; д) .

Выполнив задание 41.3. и заменив получившиеся ответы буквами из таблицы, Вы откроете фамилию математика – автора теоремы:

Е

Памятник учёному

сли степенной ряд сходится в точке , то он сходится, и притом абсолютно, для всех х, удовлетворяющих неравенству: .

Его работы в теории рядов фундаментальны. Огромное число понятий и теорем в различных областях математики носит его имя. За свою короткую жизнь этот учёный сделал важнейшее для науки открытие: доказал, что алгебраические уравнения степени выше четвёртой в общем случае неразрешимы в радикалах.

На его родине знаменитому математику установлен необычный памятник. По круто поднимающейся гранитной глыбе молодой человек с одухотворённым лицом шагает ввысь, переступая через два отвратительных чудовища. Что они символизируют? Одни математики, шутя, говорят, что они изображают уравнения пятой степени и эллиптические функции, побеждённые учёным. Другие утверждают, что скульптор воплотил в образе чудовищ социальную несправедливость. Именно с ней всю жизнь боролся учёный. Только в этой трактовке автор памятника погрешил против истины: не математик победил эти чудовища, а они погубили его…

Фамилия математика – автора теоремы:

а)	б)	в)	г)	д)

Карта ответов:

Э	У	Е	Р	Т
	7	1	3
И	А	В	Й	Ь
0	6			4
Л	М	Н	Б	О
		10		2

 41.4. Выучите определение интервала сходимости степенного ряда. Выясните, какова техника его нахождения.

41.5. Найдите интервал сходимости степенного ряда:

а) ; б) ; в) ; г) ; д) .

Методические указания по выполнению работы:

Для успешного решения задач необходимо знание следующего теоретического материала:

Функциональный ряд вида , членами которого являются степенные функции аргумента х, называется степенным ( – действительная переменная, действительные числа , , ,…, ,… - коэффициенты степенного ряда).

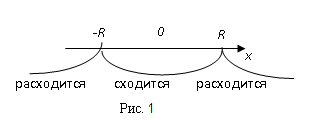
Радиусом сходимости R степенного ряда называется неотрицательное действительное число или + (0 R + ), удовлетворяющее условиям: при всех x, для которых | | < R степенной ряд сходится; при всех х, для которых | | > R, степенной ряд расходится.

Если степенной ряд сходится лишь в одной точке , то его радиус сходимости равен 0: R=0.

Если степенной ряд сходится при всех действительных значениях переменной (во всех точках числовой оси), то его радиус сходимости равен + : R= + .

У любого степенного ряда есть радиус сходимости, найти который позволяет следующая теорема.

Теорема: Если для степенного ряда существуют конечные или бесконечные пределы или , равные l, то радиус сходимости степенного ряда находится по формуле:

R= .

Заметим, что находить l можно, фактически осуществляя ту же последовательность действий, что и в алгоритмах, предназначенных для исследования сходимости положительных рядов по признакам Даламбера и Коши. При этом роль общего члена положительного ряда будет играть коэффициент степенного ряда.

Рассмотрим примеры нахождения радиуса сходимости степенного ряда.

Пример 1. Найдите радиус сходимости степенного ряда .

Решение. Радиус сходимости степенного ряда будем искать по формуле: R= . Поскольку коэффициент степенного ряда содержит выражение , то для нахождения l применим формулу: l = , аналогичную формуле признака Даламбера. Фактически воспользуемся соответствующим алгоритмом. Для этого:

1. найдём коэффициент : = ;

2. найдём коэффициент : = = ;

3. найдём отношение коэффициентов : = : = = = = .

Таким образом, получим l= = = = = = = =9.

Следовательно, так как R = , а l= 9, то R = .

Ответ: R = .

Если для степенного ряда l=0, то его радиус сходимости R равен + : R= + .

Если для степенного ряда l=+ , то его радиус сходимости R равен 0: R= 0.

Пример 2. Найдите радиус сходимости степенного ряда .

Решение. Радиус сходимости степенного ряда будем искать по формуле: R= . Поскольку коэффициент степенного ряда представляет собой n – ую степень выражения : , то для нахождения l применим формулу: l = , аналогичную формуле признака Коши. Фактически воспользуемся соответствующим алгоритмом. Для этого:

1. найдём коэффициент : ;

2. найдём : .

Таким образом, получим .

Следовательно, если , то .

Ответ: .

Если R - радиус сходимости степенного ряда , то множество точек х, удовлетворяющих неравенству , называется интервалом сходимости I степенного ряда. Значит, если R – радиус сходимости степенного ряда , то его интервал сходимости находится следующим образом:

Пример 3. Найдите интервал сходимости степенного ряда .

Решение. Интервал сходимости степенного ряда определяется формулой: Выясним, чему равен радиус сходимости данного степенного ряда. Искать его будем по соотношению: . Для нахождения l применим формулу: l = , аналогичную формуле признака Даламбера. Фактически воспользуемся соответствующим алгоритмом. Для этого:

1. найдём коэффициент : ;

2. найдём коэффициент : ;

3. найдём отношение коэффициентов : .

Таким образом, получим (при раскрытии неопределённости использовали правило Лопиталя). Следовательно, так как , а , то .

Применяя формулу для нахождения интервала сходимости степенного ряда: , получим: .

Ответ: .

Список литературы:

1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский. - М.: Издательский центр "Академия", 2012. – 320с. – Глава 10, п.10.3, стр. 253 – 258.

2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– М.: Наука, 1989. – 576 с. – Глава 13, § 81, стр. 435-440.