Раздел 3. Основы математического анализа

Тема 3.7. Обыкновенные дифференциальные уравнения Задание 48. Решение дифференциальных уравнений 1-го порядка – 1 ч.

Цель: формирование умений решать дифференциальные уравнения первого порядка: простейшие, с разделёнными и разделяющимися переменными, однородные, линейные.

Задание для самостоятельной внеаудиторной работы:

 48.1. Какие основные виды дифференциальных уравнений первого порядка Вам известны? Какова техника их решения?

48.2. Определите вид дифференциального уравнения и найдите его решение:

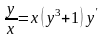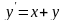а) ; б) ; в) , ; г) .

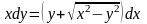48.3. Определите вид дифференциального уравнения и найдите его решение:

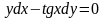а) б) ; в) .

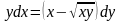Методические указания по выполнению работы:

Если в задании не указан вид дифференциального уравнения, проанализируйте, к какому из ранее изученных видов данное уравнение относится или приводится путём преобразований. При преобразованиях Вы имеете право:

• переносить слагаемые из одной части уравнения в другую с противополодным знаком;

• использовать правило: если множитель в одной части уравнения находится в числителе, то в другую часть его можно записать в знаменатель и наоборот;

• представлять как и наоборот .

Вы можете получить:

1. простейшее дифференциальное уравнение – уравнение вида ( в левой части уравнения – только , в правой – только члены, содержащие х).

Если в решении возникают проблемы – перечитайте методические указания к заданию 45.

2. дифференциальное уравнение с разделяющимися переменными - всегда приводится к виду . То есть, все члены, содержащие х, можно сгруппировать в левой части уравнения, у – в правой.

Если в решении возникают сложности – перечитайте методические указания к заданию 45.

3. однородное дифференциальное уравнение – в нём нельзя «разделить» переменные х и у, но степень каждого слагаемого при dx и dy одинакова.

Подробный алгоритм решения Вы найдёте в методических указаниях к заданию 46.

4. линейные дифференциальные уравнения – уравнение вида . Если при у Вас коэффициент не 1, разделите обе части уравнения на стоящий при коэффициент.

Указания к решению таких уравнений Вы найдёте в методических указаниях к заданию 47.

Список литературы:

1. Григорьев В.П. Элементы высшей математики: учеб. для студентов СПО / В.П. Григорьев, Ю.А. Дубинский. – М.: Академия, 2012.-320 с. - Глава 11, п. 11.2, стр. 269 – 276.

2. Валуцэ И.И. Математика для техникумов: учеб. пособие. / И.И. Валуцэ, Г.Д. Дилигул – М.: Наука, 1989.-576 с. - Глава 10, §59 - 61, стр. 321 – 335.

3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 6, §2-3, стр. 375 – 393.

Раздел 3. Основы математического анализа

Тема 3.7. Обыкновенные дифференциальные уравнения Задание 49. Решение дифференциальных уравнений второго порядка – 1 ч.

Цель: формирование умений решать дифференциальные уравнения второго порядка: простейшие, линейные однородные с постоянными коэффициентами.

Задание для самостоятельной внеаудиторной работы:

 49.1. Какие дифференциальные уравнения называют простейшими второго порядка? Какова техника их решения?

49.2. Решите простейшие дифференциальные уравнения второго порядка:

а) 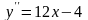; б) .

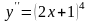49.3. Найдите частное решение простейших дифференциальных уравнений второго порядка:

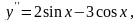
а) 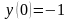; б) .

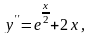
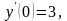
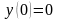 49.4. Какие дифференциальные уравнения называют линейными однородными (ЛОДУ) второго порядка с постоянными коэффициентами? Какова техника их решения?

49.5. Решите ЛОДУ II порядка с постоянными коэффициентами:

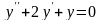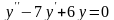а) ; б) ; в) .

 49.6. Решите дифференциальные уравнения второго порядка:

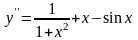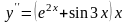а) ; б) ; в) , .

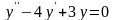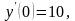
Методические указания по выполнению работы:

Выделяют следующие виды дифференциальных уравнений второго порядка:

1. Простейшие дифференциальные уравнения второго порядка - уравнения вида: .

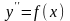Метод решения: двукратное интегрирование по переменной х.

Пример 1. Найдите решение дифференциального уравнения .

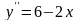Решение. Поскольку перед нами простейшее дифференциальное уравнение второго порядка, найдем сначала по формуле: .

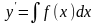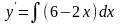
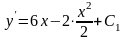или 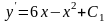, где С₁ – константа.

Для нахождения искомой функции у найдем интеграл от по переменной х:

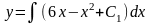
или 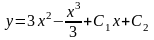, где С₁ и С₂ – константы.

Полученная функция является общим решением дифференциального уравнения . Ответ: .

Обратите внимание, что общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные С₁ и С₂.

Для нахождения решения задачи Коши можно использовать следующий алгоритм:

1. Найдите по формуле: .

2. Воспользовавшись первым начальным условием ( 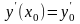), найдите значение константы С₁ и подставьте его в функцию .

3. Найдите функцию у, взяв интеграл от по переменной х.

4. Воспользовавшись вторым начальным условием ( ), найдите значение константы С₂ и подставьте его в функцию 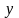. Полученная функция будет являться частным решением исходного дифференциального уравнения.

Пример 2. Найдите решение задачи Коши: 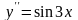, если пр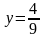и и .

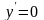Решение. 1. Найдем .

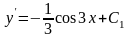2. Воспользуемся первым начальным условием: при . Подставим эти числа в функцию : 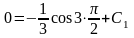. Поскольку , получим, что .

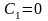Подставим найденное значение С₁ в функцию : 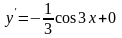или .

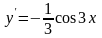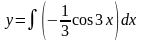
3. Найдем функцию у: 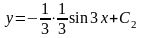или .

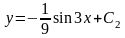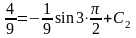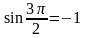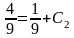
4. Воспользуемся вторым начальным условием: при . Подставим эти числа в функцию : . Поскольку , получим: 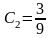или .

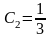Найденное значение константы С₂ подставим в функцию : 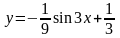. Полученная функция является частным решением исходного дифференциального уравнения при заданных начальных условиях.

Ответ: .

2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами - уравнение вида 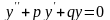, где p и q – постоянные величины.

Для нахождения решения дифференциальных уравнений такого вида будем составлять характеристическое уравнение: , где k – некоторая новая переменная. Характеристическое уравнение является квадратным относительно k.

В зависимости от числа и вида корней данного характеристического уравнения, решение исходного дифференциального уравнения можно представить в виде таблицы 49.1:

Таблица 49.1