
- •Часть 3
- •Содержание
- •Пояснительная записка
- •Каждое задание включает в себя:
- •Рекомендации по работе с учебно-методическим пособием
- •Рекомендации по выполнению разных видов
- •Как самостоятельно изучить теоретический материал
- •Как составить обобщающую таблицу по теме
- •3. Как решать задачи (методика д. Пойа)
- •4. Как подготовить доклад
- •Доклад на тему «_______________________» Дисциплина: Элементы высшей математики Выполнил: студент группы ___
- •5. Как создать презентацию
- •Задания для самостоятельной работы
- •Раздел 3. Основы математического анализа
- •Тема 3.6. Теория рядов Задание 38. Применение необходимого признака сходимости и свойств рядов – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.6. Теория рядов Задание 39. Исследование сходимости числовых положительных рядов – 3 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.6. Теория рядов Задание 40. Исследование абсолютной и условной сходимости знакочередующихся рядов – 2 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.6. Теория рядов Задание 41. Нахождение радиуса и интервала сходимости степенного ряда – 1 ч.
- •Памятник учёному
- •Раздел 3. Основы математического анализа
- •Тема 3.6. Теория рядов Задание 42. Разложение функций в ряд Маклорена – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.6. Теория рядов Задание 43. Систематизация знаний по теме «Ряды» – 1ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.7. Обыкновенные дифференциальные уравнения Задание 44. Задачи, решаемые с помощью дифференциальных уравнений – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.7. Обыкновенные дифференциальные уравнения Задание 45. Решение дифференциальных уравнений с разделёнными и разделяющимися переменными – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.7. Обыкновенные дифференциальные уравнения Задание 46. Решение однородных дифференциальных уравнений – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.7. Обыкновенные дифференциальные уравнения Задание 47. Решение линейных дифференциальных уравнений – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.7. Обыкновенные дифференциальные уравнения Задание 48. Решение дифференциальных уравнений 1-го порядка – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.7. Обыкновенные дифференциальные уравнения Задание 49. Решение дифференциальных уравнений второго порядка – 1 ч.
- •Решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •Раздел 3. Основы математического анализа
- •Тема 3.7. Обыкновенные дифференциальные уравнения Задание 50. Виды дифференциальных уравнений и методы их решения – 1 ч.
- •Раздел 4. Основы теории комплексных чисел
- •Тема 4.1. Формы комплексных чисел Задание 51. Действия над комплексными числами в алгебраической форме. Решение квадратных уравнений – 1 ч.
- •Пример 1. Для комплексных чисел и найдите: а) ; б) ; в) .
- •Пример 3. Решите уравнение: .
- •Раздел 4. Основы теории комплексных чисел
- •Тема 4.1. Формы комплексных чисел Задание 52. Действия над комплексными числами в тригонометрической форме – 1 ч.
- •Пример 1. Изобразите на комплексной плоскости числа: , , .
- •Пример 2. Для комплексных чисел , найдите: а) ; б) ; в) ; г) .
- •Раздел 4. Основы теории комплексных чисел
- •Тема 4.1. Формы комплексных чисел Задание 53. Действия над комплексными числами в показательной форме – 1 ч.
- •Раздел 4. Основы теории комплексных чисел
- •Тема 4.1. Переход между различными формами комплексных чисел Задание 54. Переход от алгебраической формы к тригонометрической и показательной и обратно – 2 ч.
- •Раздел 5. Использование пакетов прикладных программ при решении задач высшей математики
- •Критерии оценки выполнения самостоятельной внеаудиторной работы
- •Список рекомендуемой литературы
Раздел 3. Основы математического анализа
Тема 3.7. Обыкновенные дифференциальные уравнения Задание 45. Решение дифференциальных уравнений с разделёнными и разделяющимися переменными – 1 ч.
Цель: формирование умений решать дифференциальные уравнения первого порядка: простейшие, с разделёнными и разделяющимися переменными.
Задание для самостоятельной внеаудиторной работы:
45.1. Какие дифференциальные уравнения называют простейшими первого порядка? Какова техника их решения?
45.2. Решите простейшее дифференциальное уравнение первого порядка:
а)
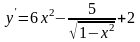 ;
б)
;
б)
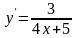 ;
в)
;
в)
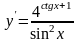 ;
г)
;
г)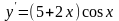 .
.
45.3. Найдите частное решение простейшего дифференциального уравнения первого порядка:
а)
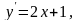
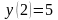 ;
б)
;
б)
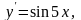
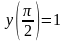 .
.
45.4. Какие дифференциальные уравнения первого порядка называют уравнениями с разделёнными и разделяющимися переменными? Какова техника их решения?
45.5. Решите дифференциальное уравнение с разделёнными и разделяющимися переменными:
а)
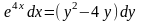 ;
б)
;
б)
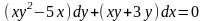 ;
в)
;
в)
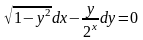 .
.
45.6. Найдите решение задачи Коши:
а)
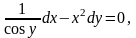
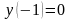 ;
б)
;
б)
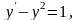
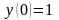 .
.
45.7. Определите численность населения России через 5 лет, считая, что скорость прироста населения пропорциональна его количеству (коэффициент пропорциональности k = -0,0006), и зная, что в население России в начале 2010 года составляло 141,9 млн. человек, а прирост населения за 2010 год был равен (-0,06)%.
Методические указания по выполнению работы:
Выделяют следующие виды дифференциальных уравнений первого порядка:
1.
Простейшие дифференциальные
уравнения - уравнения вида
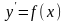 .
.
Метод
решения: взять интеграл от
правой и левой части по переменной х:
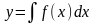 .
.
Пример
1. Найдите решение дифференциального
уравнения
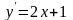 .
.
Решение. Поскольку перед нами простейшее дифференциальное уравнение первого порядка, найдем его решение по формуле :
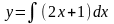 ;
;
у
=
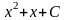 - общее решение дифференциального
уравнения
.
- общее решение дифференциального
уравнения
.
Ответ: у = .
Пример
2. Найдите частное решение уравнения
,
если
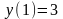 .
.
Решение. Общее решение заданного дифференциального уравнения имеет вид:
у
=
(см. пример 1) . Воспользуемся начальными
условиями:
,
следовательно, при
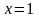
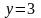 .
Подставим эти числа в общее решение:
.
Подставим эти числа в общее решение:
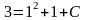 .
Выразим из данного уравнения С:
.
Выразим из данного уравнения С:
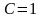 .
.
Подставив
найденное значение С в общее решение
у =
,
получим следующее частное решение
дифференциального уравнения: у =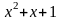 .
.
Ответ: у = .
2.
Дифференциальные уравнения
с разделёнными переменными
- уравнения вида
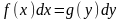 .
.
Если дифференциальное уравнение путем преобразований можно привести к виду , то оно называется дифференциальным уравнением с разделяющимися переменными.
Метод
решения: проинтегрировать
обе части уравнения:
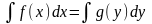 .
.
Пример
3. Найдите решение дифференциального
уравнения:
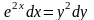 .
.
Решение. Данное дифференциальное уравнение представляет собой уравнение с разделенными переменными. Проинтегрируем обе части уравнения:
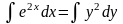 .
Тогда
.
Тогда
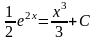 - общее решение
дифференциального уравнения
.
- общее решение
дифференциального уравнения
.
Ответ: .
Для решения уравнений с разделяющимися переменными целесообразно использовать следующий алгоритм:
Если в уравнении встречается
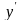 ,
то представьте его как
,
то представьте его как
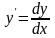 .
.Произведите разделение переменных (в одной части при dx соберите выражения, содержащие только переменную х; в другой части при dу соберите выражения, содержащие только переменную у).
Почленно проинтегрируйте обе части уравнения с разделёнными переменными.
Выпишите в ответе получившееся общее решение дифференциального уравнения.
Пример
4. Найдите решение дифференциального
уравнения:
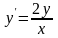 .
.
Решение.
1. Данное уравнение – дифференциальное
уравнение с разделяющимися переменными.
Представим
,
тогда
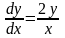 или
или
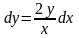 .
.
2.
Будем собирать множители с у в левой
части, с х – в правой:
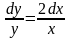 .
.
3.
Интегрируя обе части, получим:
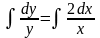 или
или
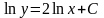 - общее решение.
- общее решение.
Ответ: .
Список литературы:
1. Григорьев В.П. Элементы высшей математики: учеб. для студентов СПО / В.П. Григорьев, Ю.А. Дубинский. – М.: Академия, 2012.-320 с. - Глава 11, п. 11.2, стр. 269 – 273.
2. Валуцэ И.И. Математика для техникумов: учеб. пособие. / И.И. Валуцэ, Г.Д. Дилигул – М.: Наука, 1989.-576 с. - Глава 10, §59 - 61, стр. 321 – 335.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 6, §2-3, стр. 375 – 393.
